SystemCache и MemoryInUse - кто-нибудь может объяснить это поведение?
Этот вопрос вдохновлен вопросом утечек памяти в Mathematica из-за внутреннего кэширования результатов промежуточных вычислений. Все это недокументировано, но важно для всех, кто выполняет вычисления с интенсивным использованием памяти.
Пытаясь понять логику внутреннего механизма кэширования, я обнаружил что-то интересное. Учтите следующее:
$HistoryLength = 0;
(*dummy command for loading of the Root package*)
Root[# &, 1];
d = 13;
f[z_, i_] := Sum[(2 Mod[Floor[(i - 1)/2^k], 2] - 1) z^(d - k), {k, 0, d}];
(memLog = Flatten[
Table[Root[f[z, i], j]; {SessionTime[], MemoryInUse[]/1024.^2}, {j, 1,
d}, {i, 1, 2^d}], 1];) // Timing
pl1 = ListLinePlot[memLog,
FrameLabel -> {"SessionTime, sec", "MemoryInUse, Mb"}, PlotRange -> All,
Frame -> True, Axes -> False]
pl2 = ListLinePlot[memLog[[All, 2]],
FrameLabel -> {"Point", "MemoryInUse, Mb"}, PlotRange -> All, Frame -> True,
Axes -> False]
В новой сессии ядра вывод на моей машине (Mathematica 7.0.1 для Windows) всегда выглядит следующим образом:
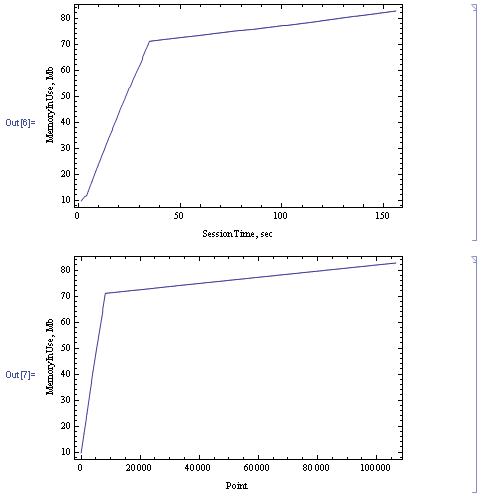
Кто-нибудь может объяснить, почему происходит разрыв кривой возле точки с номером 8400?
1 ответ
Точка, в которой происходит изменение наклона, - нет. 8192. Это равно 2^13, что является верхней границей самого быстрого из ваших индексов таблицы, i, Когда ММА приходит в этот момент, он рассчитал все возможные f[z, i] ценности. Поскольку этот вызов не зависит от j, следующее значение j (2) будет генерировать тот же диапазон (f[z, 1], ..., f[z, 8192]) снова. Я предполагаю, что именно здесь начинается внутреннее кэширование и требуется меньше дополнительной памяти.