Пробелы в графике кусочно-зависимых функций в Matlab

Question

Я хочу построить кусочную функцию, но не хочу, чтобы появлялись пробелы

на стыках, например:

t=[1:8784];

b=(26.045792 + 13.075558*sin(0.0008531214*t - 2.7773943)).*((heaviside(t-2184))-(heaviside(t-7440)));

plot(b,'r','LineWidth', 1.5);grid on

не должно быть никаких пробелов, появляющихся на графике между этими тремя интервалами, но они есть.

Я хочу, чтобы график был непрерывным без пробелов.

Любые предложения о том, как этого добиться.

Заранее спасибо.

РЕДАКТИРОВАТЬ
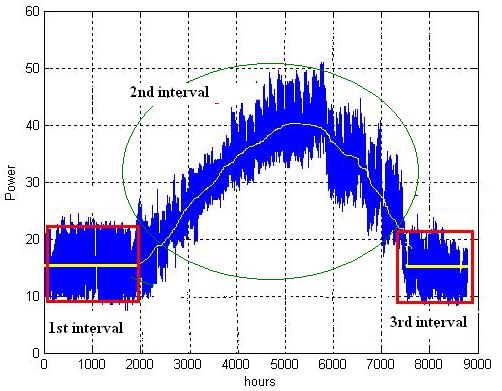
На самом деле, моя цель - найти несущую функцию, выделенную желтым цветом на рисунке ниже. Я делю весь интервал на 3 интервала: 1-константа 2-синусоидальная 3-константа, затем я хочу найти общую функцию из этих трех функций

Answer 1

Конечно, есть "пробелы". Составная функция тождественно равна нулю для всех t<2184 и для всех t>7440. Отношения могут быть ненулевыми только внутри этого интервала. И вы не выбрали функцию, которая равна нулю на конечных точках, так как вы можете ожидать, что не будет "пробелов"?

Какие значения принимает ваша функция в конечных точках интервала?

>> t = [2184 7440];
>> (26.045792 + 13.075558*sin(0.0008531214*t - 2.7773943))
ans =
       15.689       20.616

Так что посмотрите на функцию шляпы часть этого. Я буду ленивым и пользуюсь ezplot.

>> ezplot(@(t) ((heaviside(t-2184))-(heaviside(t-7440))),[0,8784])

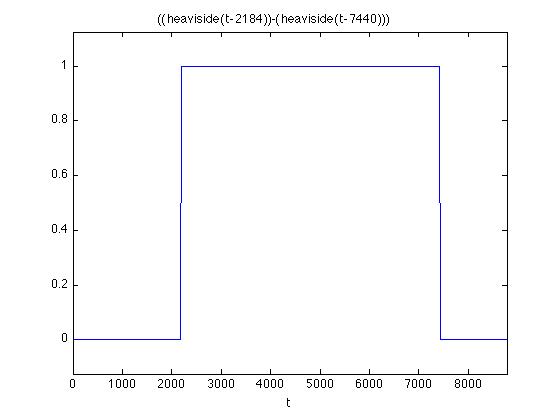
Теперь, скомбинируйте это, умножив на триггер, и, конечно, результат будет равен нулю за пределами этой области.

>> ezplot(@(t) (26.045792 + 13.075558*sin(0.0008531214*t - 2.7773943)).*((heaviside(t-2184))-(heaviside(t-7440))),[0,8784])

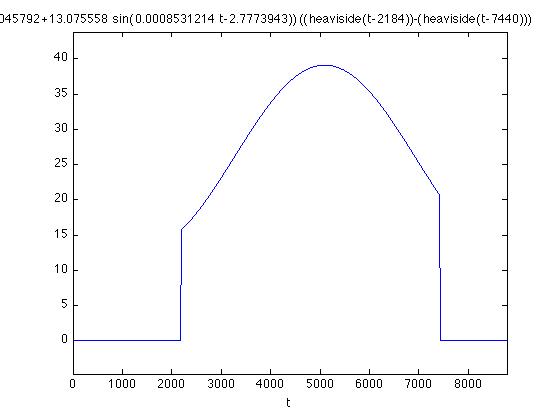
Но если вашей целью является какая-то непрерывная функция в двух выбранных точках в функции шляпы, вам нужно выбрать триггерную часть так, чтобы она равнялась нулю в тех же двух точках. Математика не пишется математики. Желание, чтобы вы получили непрерывную функцию, не сделает это так.

Так есть ли у вас реальный вопрос, как выбрать эту внутреннюю часть (сегмент) так, чтобы конечный результат был непрерывным? Если так, то нам нужно знать, почему вы выбрали там произвольные константы. Конечно, эти числа, {26.045792, 13.075558, 0.0008531214, 2.7773943} все должны иметь какое-то значение для вас. И если они важны, то как мы можем сделать результат непрерывной функцией?

Возможно, и я просто догадываюсь, что вам нужен какой-то другой результат, такой, чтобы функция не была тождественно нулевой вне этих границ. Возможно, вы хотите экстраполировать как постоянную функцию вне этих точек. Но чтобы помочь вам, вы должны помочь нам.