Существует ли общий способ преобразования однозначной контекстно-свободной грамматики в грамматику LALR(1)?

Question

Я пытаюсь создать парсер LALR(1) для следующей грамматики и нахожу некоторые сдвиги / сокращения конфликтов.

S := expr
expr := lval | ID '[' expr ']' OF expr
lval := ID | lval '[' expr ']'

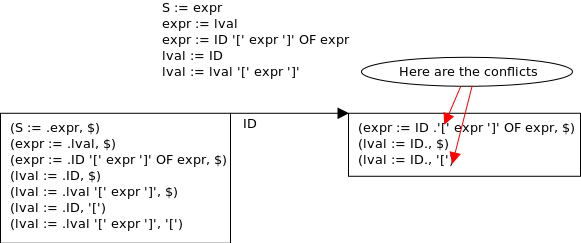
Поэтому синтаксический анализатор не может правильно проанализировать строку "ID[ID]". Мои вопросы

1. Существуют ли общие способы преобразования таких не-LALR(1) грамматик в LALR(1) грамматику?
2. Если две грамматики генерируют абсолютно одинаковые языки и мы знаем, что одна не является LALR(1), можем ли мы знать, является ли другая LALR(1)?

Упомянутая выше грамматика является лишь примером, и я действительно хочу знать общие способы решения этих грамматических проблем. Любые предложения или рекомендации по чтению приветствуются.

Заранее спасибо.

Answer 1

1 Существуют ли общие способы преобразования таких не-LALR(1) грамматик в LALR (1) грамматику?

Нет. Может или не может быть возможно преобразовать произвольную контекстно-свободную грамматику (CFG) в грамматику LALR (1). Для этого нет общего алгоритма, даже если вы как-то знаете, что это возможно. Более того, если у вас есть грамматика CFG и LALR(1), вы не можете сказать, распознают ли они один и тот же язык. (Хуже того, не существует алгоритма, который бы даже сообщал вам, распознает ли произвольный CFG каждую возможную строку для своего алфавита.)

2 Если две грамматики генерируют абсолютно одинаковые языки и мы знаем, что одна не является LALR(1), можем ли мы знать, является ли другая LALR(1)?

Опять нет. Как и выше, не существует алгоритма, который мог бы проверить, что две грамматики генерируют один и тот же язык, но даже предполагая, что вы знаете, что две грамматики генерируют один и тот же язык, тот факт, что одна из них не является LALR(1), ничего не говорит о другом один.

Однако есть один полезный результат. Если у вас есть грамматика LALR(k) с конечным k > 1, то вы можете сгенерировать грамматику LALR (1). Другими словами, не существует такого понятия, как язык LALR(k) для k > 1; если язык имеет грамматику LALR(k), он имеет грамматику LALR(k') для любого k' такого, что 1 ≤ k'

Это не поможет вам с вашей грамматикой, потому что конфликт не может быть устранен путем увеличения предвкушения к любой конечной ценности.

Однако существует простой способ избавиться от этого конкретного конфликта "сдвиг-уменьшение", и этот метод часто работает. Рассмотрим два противоречивых правила:

lval := lval '[' expr ']'
expr := ID   '[' expr ']' OF expr

Проблема в том, что в первом случае ID должен быть уменьшен до lval немедленно (или, по крайней мере, до следующего expr сокращается), но во втором случае его нельзя уменьшить до lval, Но мы не можем сказать, в каком случае мы находимся, пока мы не уменьшим expr и столкнуться с OF (или нет).

Если бы мы могли закончить lval производство, не делая интерьер lval сокращение, то у нас не будет проблем, потому что фактическое сокращение произойдет, когда токен, следующий за ] виден

Возможно, для этого есть технический термин, но я его не знаю. Я всегда описывал это как "отсрочка сокращения", и во многих случаях это не очень сложно:

lval' := ID `[` expr `]`
      |  lval' `[` expr `]`
lval  := ID
      |  lval'
expr  := lval
      |  ID '[' expr ']' OF expr