Мои спектры мощности правдоподобны? сравнение между lomb-scargle и fft (scipy.signal и numpy.fft)
Может ли кто-нибудь любезно указать, почему я получаю совсем другие результаты?
Есть много пиков, которые не должны появляться. На самом деле, должен быть только один пик.
Я новичок в Python, и все комментарии о моем коде ниже приветствуются.
Тестовые данные здесь. введите описание ссылки здесь
Вы можете напрямую wget https://clbin.com/YJkwr,
Его первый столбец - время прибытия серии фотонов. Источник света испускает фотоны случайным образом. Общее время 55736 секунд и 67398 фотонов. Я пытаюсь обнаружить некоторую периодичность интенсивности света.
Мы можем сопоставить время и интенсивность света пропорционально количеству фотонов в каждом отсчете времени.
Я попробовал numpy.fft и lomb-scargle of scipy.signal, чтобы получить спектр мощности, но получил очень разные результаты.
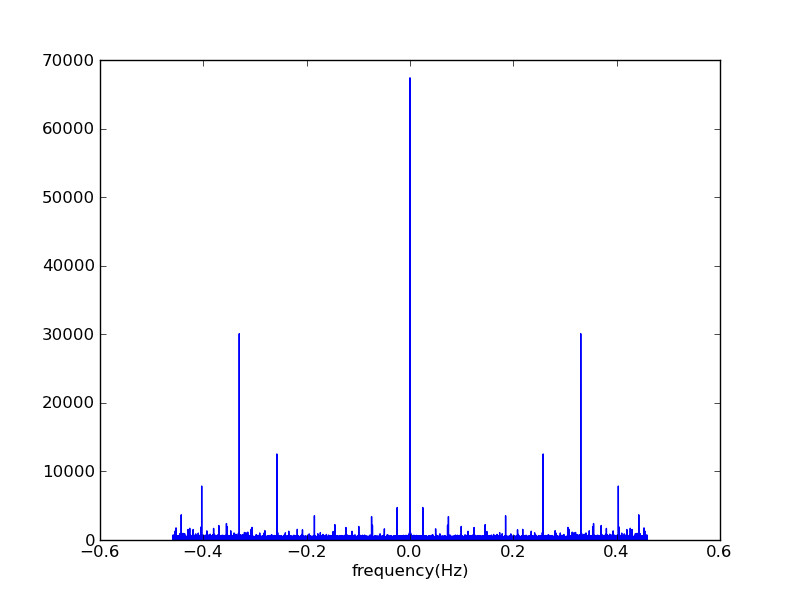
быстрое преобразование Фурье
import pylab as pl
import numpy as np
timepoints=np.loadtxt('timesequence',usecols=(0,),unpack=True,delimiter=",")
binshu=50000
interd=54425./binshu
t=np.histogram(timepoints,bins=binshu)[0]
sp = np.fft.fft(t)
freq = np.fft.fftfreq(len(t),d=interd)
freqnum = np.fft.fftfreq(len(t),d=interd).argsort()
pl.xlabel("frequency(Hz)")
pl.plot(freq[freqnum],np.abs(sp)[freqnum])
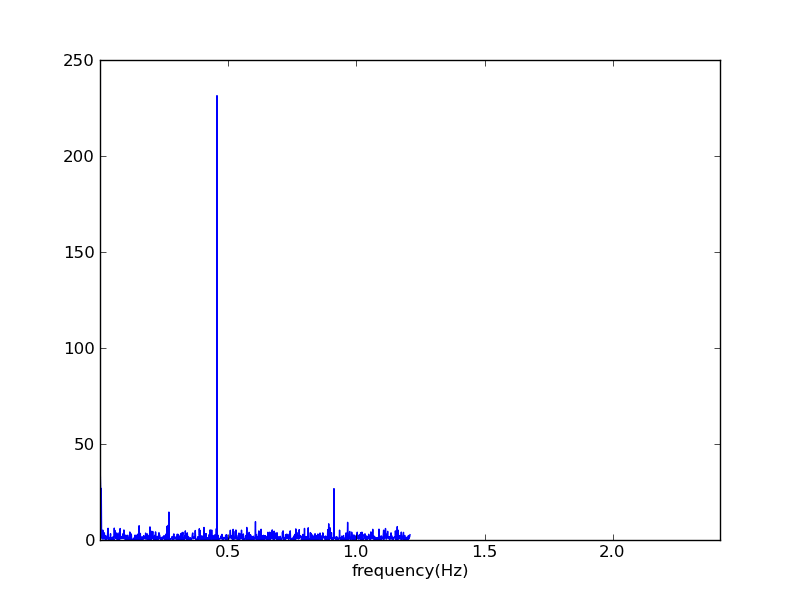
Lomb-scargle
timepoints=np.loadtxt('timesequence',usecols=(0,),unpack=True,delimiter=",")
binshu=50000
intensity=np.histogram(timepoints,bins=binshu)[0].astype('float64')
middletime=np.histogram(timepoints,bins=binshu)[1][1:binshu+1]-np.histogram(timepoints,bins=binshu)[1][3]*0.5
freq1=1./(timepoints.max()-timepoints.min())
freq2=freq1*len(timepoints)
freqs=np.linspace(freq1,freq2,1000)
pm1=spectral.lombscargle(middletime,intensity,freqs)
pl.xlabel("frequency(Hz)")
pl.plot(freqs,pm1)
pl.xlim(0.5*freq1,2*freq2)
pl.ylim(0,250)
pl.show()
*********************************
Спасибо, Уоррен, я ценю это. Спасибо за подробный ответ.
Вы правы, время интеграции есть, здесь оно около 1.7с.
Есть много одиночных воздействий. Каждая экспозиция стоит 1,7 с.
В одной экспозиции мы не можем точно сказать время ее прибытия.
Если временные ряды похожи на:
0 1,7 3,4 8,5 8,5
Время интегрирования последних двух фотонов 1.7s,не (8.5-3.4)sТак что я буду пересматривать часть вашего кода.
ОДНАКО мой вопрос все еще остается. Вы настраиваете несколько параметров, чтобы получить 0.024Hz Пик Ломбарда в некоторой степени. И вы используете это, чтобы вести ваши параметры в FFT.
Если вы не знаете номер 0.024, может быть, вы можете использовать разные параметры, чтобы получить другой самый высокий пик?
Как гарантировать каждый раз, когда мы можем получить право num_ls_freqs? Вы можете увидеть, если мы выбираем разные num_ls_freqs, самый высокий пик сдвигов.
Если у меня много временных рядов, каждый раз мне приходится указывать разные параметры? И как их получить?
2 ответа
Похоже, 50000 корзин недостаточно. Если вы измените binshuвы увидите, что расположение шипов меняется, и не только немного.
Перед тем, как погрузиться в FFT или Lomb-Scargle, я посчитал полезным сначала изучить необработанные данные. Вот начало и конец файла:
0,1,3.77903
0,1,4.96859
0,1,1.69098
1.74101,1,4.87652
1.74101,1,5.15564
1.74101,1,2.73634
3.48202,1,3.18583
3.48202,1,4.0806
5.2229,1,1.86738
6.96394,1,7.27398
6.96394,1,3.59345
8.70496,1,4.13443
8.70496,1,2.97584
...
55731.7,1,5.74469
55731.7,1,8.24042
55733.5,1,4.43419
55733.5,1,5.02874
55735.2,1,3.94129
55735.2,1,3.54618
55736.9,1,3.99042
55736.9,1,5.6754
55736.9,1,7.22691
Есть кластеры одинакового времени прибытия. (Это необработанный вывод фотонного детектора или этот файл каким-то образом был предварительно обработан?)
Таким образом, первый шаг - объединить эти кластеры в одно число за один раз, чтобы данные выглядели так (время, количество), например:
0, 3
1.74101, 3
3.48202, 2
5.2229, 1
etc
Следующее выполнит этот подсчет:
times, inv = np.unique(timepoints, return_inverse=True)
counts = np.bincount(inv)
Сейчас times массив увеличивающихся уникальных значений времени, и counts число фотонов, обнаруженных в это время. (Обратите внимание, что я предполагаю, что это правильная интерпретация данных!)
Посмотрим, будет ли выборка примерно одинаковой. Массив времен взаимодействия
dt = np.diff(times)
Если выборка была абсолютно равномерной, все значения в dt будет таким же. Мы можем использовать тот же шаблон, что и выше на timepoints найти уникальные значения (и частоту их появления) в dt:
dts, inv = np.unique(dt, return_inverse=True)
dt_counts = np.bincount(inv)
Например, вот что dts выглядит, если мы напечатаем это:
[ 1.7 1.7 1.7 1.7 1.74 1.74 1.74 1.74
1.74 1.74 1.74088 1.741 1.741 1.741 1.741
1.741 1.741 1.741 1.74101 1.74102 1.74104 1.7411
1.7411 1.7411 1.7411 1.7411 1.742 1.742 1.742
1.746 1.75 1.8 1.8 1.8 1.8 3.4 3.4
3.4 3.4 3.48 3.48 3.48 3.48 3.48 3.482
3.482 3.482 3.482 3.482 3.4821 3.483 3.483 3.49
3.49 3.49 3.49 3.49 3.5 3.5 5.2 5.2
5.2 5.2 5.22 5.22 5.22 5.22 5.22 5.223
5.223 5.223 5.223 5.223 5.223 5.23 5.23 5.23
5.3 5.3 5.3 5.3 6.9 6.9 6.9 6.9
6.96 6.96 6.964 6.964 6.9641 7. 8.7 8.7
8.7 8.7 8.7 8.71 10.4 10.5 12.2 ]
(Кажущиеся повторяющиеся значения на самом деле разные. Полная точность чисел не показана.) Если бы выборка была абсолютно равномерной, в этом списке был бы только один номер. Вместо этого мы видим группы чисел без очевидных доминирующих значений. (Преобладание кратно 1,74- это характеристика детектора?)
Основываясь на этом наблюдении, мы начнем с Lomb-Scargle. Сценарий ниже включает в себя код для вычисления и построения периодограммы Ломба-Скарлга (times, counts) данные. Частоты даны lombscargle варьироваться от 1/trange, где trange полный промежуток времени данных, чтобы 1/dt.min(), Количество частот 16000 (num_ls_freqs в сценарии). Некоторые методики проб и ошибок показали, что это примерно минимальное число, необходимое для разрешения спектра. Меньше, чем это, и пики начинают двигаться вокруг. Больше чем это, и есть небольшое изменение в спектре. Расчет показывает, что существует пик в 0,0242 Гц. Другие пики являются гармониками этой частоты.
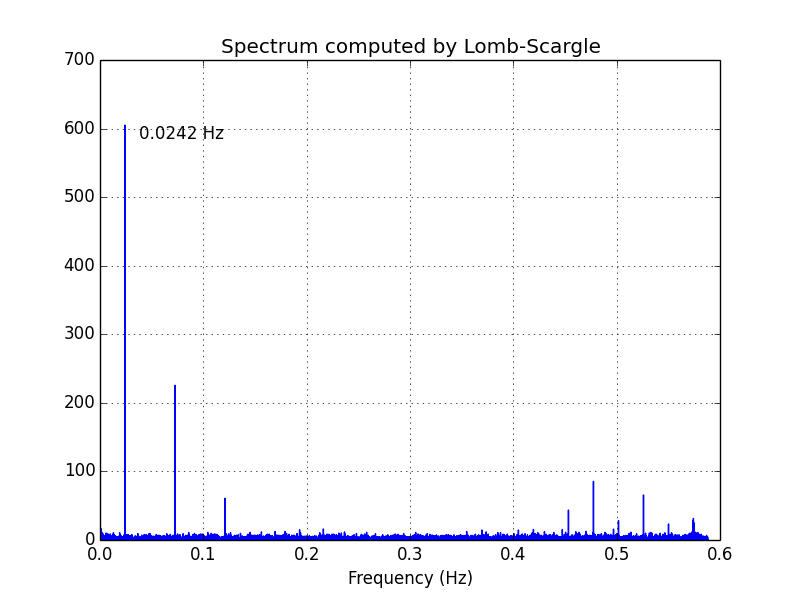
Теперь, когда у нас есть оценка основной частоты, мы можем использовать ее для выбора размера корзины в гистограмме timepoints для использования в расчете БПФ. Мы будем использовать размер бина, который приводит к передискретизации основной частоты в 8 раз. (В приведенном ниже скрипте это m. То есть мы делаем
m = 8
nbins = int(m * ls_peak_freq * trange + 0.5)
hist, bin_edges = np.histogram(timepoints, bins=nbins, density=True)
(timepoints исходный набор времени, считанный из файла; это включает много повторяющихся значений времени, как отмечено выше.)
Затем мы применяем БПФ к hist, (Мы на самом деле будем использовать numpy.fft.rfft.) Ниже приведен график спектра, рассчитанного с использованием БПФ:
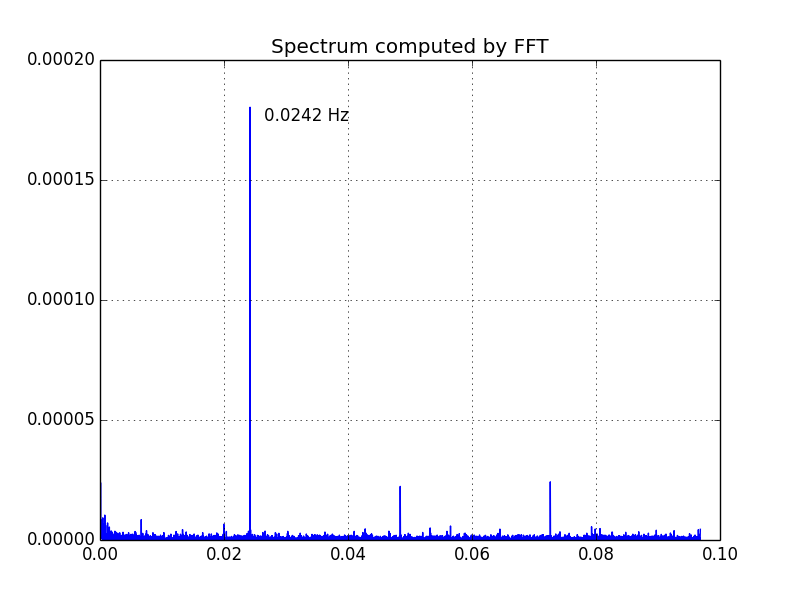
Как и ожидалось, пик составляет 0,0242 Гц.
Вот сценарий:
import numpy as np
from scipy.signal import lombscargle
import matplotlib.pyplot as plt
timepoints = np.loadtxt('timesequence', usecols=(0,), delimiter=",")
# Coalesce the repeated times into the `times` and `counts` arrays.
times, inv = np.unique(timepoints, return_inverse=True)
counts = np.bincount(inv)
# Check the sample spacing--is the sampling uniform?
dt = np.diff(times)
dts, inv = np.unique(dt, return_inverse=True)
dt_counts = np.bincount(inv)
print dts
# Inspection of `dts` shows that the smallest dt is about 1.7, and there
# are many near multiples of 1.74, but the sampling is not uniform,
# so we'll analyze the spectrum using lombscargle.
# First remove the mean from the data. This is not essential; it just
# removes the large value at the 0 frequency that we don't care about.
counts0 = counts - counts.mean()
# Minimum interarrival time.
dt_min = dt.min()
# Total time span.
trange = times[-1] - times[0]
# --- Lomb-Scargle calculation ---
num_ls_freqs = 16000
ls_min_freq = 1.0 / trange
ls_max_freq = 1.0 / dt_min
freqs = np.linspace(ls_min_freq, ls_max_freq, num_ls_freqs)
ls_pgram = lombscargle(times, counts0, 2*np.pi*freqs)
ls_peak_k = ls_pgram.argmax()
ls_peak_freq = freqs[ls_peak_k]
print "ls_peak_freq =", ls_peak_freq
# --- FFT calculation of the binned data ---
# Assume the Lomb-Scargle calculation gave a good estimate
# of the fundamental frequency. Use a bin size for the histogram
# of timepoints that oversamples that period by m.
m = 8
nbins = int(m * ls_peak_freq * trange + 0.5)
hist, bin_edges = np.histogram(timepoints, bins=nbins, density=True)
delta = bin_edges[1] - bin_edges[0]
fft_coeffs = np.fft.rfft(hist - hist.mean())
fft_freqs = np.fft.fftfreq(hist.size, d=delta)[:fft_coeffs.size]
# Hack to handle the case when hist.size is even. `fftfreq` puts
# -nyquist where we want +nyquist.
fft_freqs[-1] = abs(fft_freqs[-1])
fft_peak_k = np.abs(fft_coeffs).argmax()
fft_peak_freq = fft_freqs[fft_peak_k]
print "fft_peak_freq =", fft_peak_freq
# --- Lomb-Scargle plot ---
plt.figure(1)
plt.clf()
plt.plot(freqs, ls_pgram)
plt.title('Spectrum computed by Lomb-Scargle')
plt.annotate("%6.4f Hz" % ls_peak_freq,
xy=(ls_peak_freq, ls_pgram[ls_peak_k]),
xytext=(10, -10), textcoords='offset points')
plt.xlabel('Frequency (Hz)')
plt.grid(True)
# --- FFT plot ---
plt.figure(2)
plt.clf()
plt.plot(fft_freqs, np.abs(fft_coeffs)**2)
plt.annotate("%6.4f Hz" % fft_peak_freq,
xy=(fft_peak_freq, np.abs(fft_coeffs[fft_peak_k])**2),
xytext=(10, -10), textcoords='offset points')
plt.title("Spectrum computed by FFT")
plt.grid(True)
plt.show()
Спектр мощности - это абсолютное значение квадрата преобразования Фурье. Если к тому же вы избавитесь от значения DC в вашем БПФ, нанесите на график только положительную половину ваших результатов и вычислите ширину ячейки по выходным данным np.histogram вместо какого-то закодированного магического числа, вот что вы получите:
timepoints=np.loadtxt('timesequence',usecols=(0,),unpack=True,delimiter=",")
binshu=50000
t, _=np.histogram(timepoints,bins=binshu)
interd = _[1] - _[0]
sp = np.fft.fft(t)
freq = np.fft.fftfreq(len(t),d=interd)
n = len(freq)
pl.xlabel("frequency(Hz)")
pl.plot(freq[1:n//2],(sp*sp.conj())[1:n//2])
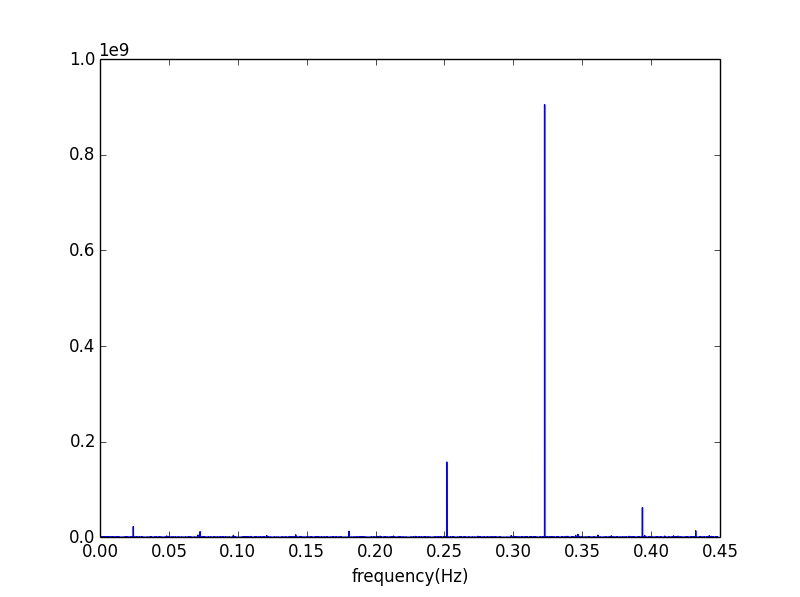
Это выглядит очень похоже на вашу периодограмму. Существует несоответствие в положении большого пика, который составляет около 0,32 в спектре, основанном на БПФ, и больше, чем 0,4x в выходном сигнале ломбарда. Не уверен, что там происходит, но я не совсем понимаю ваши расчеты частоты, особенно в случае с ломбардами...