Реализация наискорейшего спуска в Matlab

Question

Я должен реализовать метод наискорейшего спуска и проверить его на функциях двух переменных, используя Matlab. Вот что я сделал до сих пор:

x_0 = [0;1.5]; %Initial guess
alpha = 1.5; %Step size
iteration_max = 10000;
tolerance = 10e-10;

% Two anonymous function to compute 1st and 2nd entry of gradient
f = @(x,y) (cos(y) * exp(-(x-pi)^2 - (y-pi)^2) * (sin(x) - 2*cos(x)*(pi-x)));
g = @(x,y) (cos(x) * exp(-(x-pi)^2 - (y-pi)^2) * (sin(y) - 2*cos(y)*(pi-y)));

%Initiliazation
iter = 0;
grad = [1; 1]; %Gradient

while (norm(grad,2) >= tolerance)
    grad(1,1) = f(x_0(1), x_0(2));
    grad(2,1) = g(x_0(1), x_0(2));
    x_new = x_0 - alpha * grad; %New solution
    x_0 = x_new %Update old solution
    iter = iter + 1;

    if iter > iter_max
        break
    end
end

Проблема в том, что по сравнению, например, с результатами WolframAlpha, я не получаю одинаковые значения. Для этой конкретной функции я должен получить либо (3.14,3.14), либо (1.3,1.3), но я получу (0.03, 1.4).

Answer 1

Вы должны знать, что этот метод является локальным поиском и, следовательно, он может застрять в локальном минимуме в зависимости от первоначального предположения и размера шага.

• С другой первоначальной догадкой он найдет другой локальный минимум.

• Размер шага важен, потому что большой размер шага может предотвратить схождение алгоритма. Небольшой размер шага делает алгоритм действительно медленным. Вот почему вы должны адаптировать размер шагов при уменьшении значения функции.

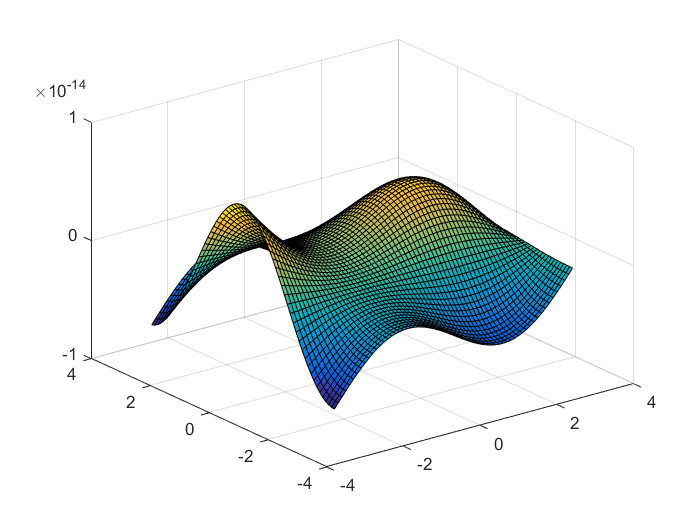
Всегда полезно понять функцию, которую вы хотите оптимизировать, построив ее (если это возможно). Функция, с которой вы работаете, выглядит следующим образом (в диапазоне [-pi pi]):

со следующими значениями параметров вы получите локальный минимум, который вы ищете.

x_0 = [2;2]; %Initial guess
alpha = 0.5; %Step size