BackPropagation Neuron Сетевой подход - Дизайн
Я пытаюсь сделать программу распознавания цифр. Я передам белое / черное изображение цифры, и мой выходной слой запустит соответствующую цифру (один нейрон срабатывает из 0 -> 9 нейронов в выходном слое). Я закончил реализацию Двумерной Сети Нейронов BackPropagation. Мои размеры топологии: [5] [3] -> [3] [3] -> 1[10]. Таким образом, это один 2-D входной слой, один 2-D скрытый слой и один 1-D выходной слой. Однако я получаю странные и неправильные результаты (средняя ошибка и выходные значения).
На этом этапе отладка отнимает много времени. Поэтому я хотел бы услышать, если это правильный дизайн, поэтому я продолжаю отладку. Вот шаги потока моей реализации:
Создайте сеть: одно смещение на каждом слое, кроме выходного (без смещения). Выходное значение смещения всегда равно 1,0, однако его веса соединений обновляются при каждом проходе, как и все другие нейроны в сети. Диапазон всех весов 0,000 -> 1000 (без негативов)
Получите входные данные (0 | ИЛИ | 1) и установите n-е значение в качестве n-го выходного значения нейрона во входном слое.
Feed Forward: на каждом нейроне 'n' в каждом слое (кроме входного слоя):
- Получить результат SUM (выходное значение * вес соединения) подключенных нейронов от предыдущего слоя к этому n-му нейрону.
- Получите TanHyperbolic - передаточную функцию - этого СУММЫ как результатов
- Установить результаты в качестве выходного значения этого n-го нейрона
Получить результаты: принять выходные значения нейронов в выходном слое
обратное распространение:
- Вычислить сетевую ошибку: на выходном уровне получить нейроны SUM ' (целевые значения - выходные значения)^2. Разделите эту сумму на размер выходного слоя. Получите его SquareRoot как результат. Средняя ошибка вычисления = (OldAverageError * SmoothingFactor * Result) / (SmoothingFactor + 1.00)
- Рассчитать градиенты выходного слоя: для каждого выходного нейрона 'n', n-й градиент = (n-е целевое значение - n-е выходное значение) * n-е выходное значение TanHyperbolic Derivative
- Рассчитайте скрытые градиенты слоя: для каждого нейрона 'n' получите SUM (TanHyperbolic Derivative от веса, идущего от этого n-го нейрона * Градиент нейрона назначения) в качестве результатов. Присвойте (Results * this nth Output Value) градиент.
- Обновление всех весов: начиная со скрытого слоя и обратно до входного слоя, для n-го нейрона: вычисление NewDeltaWeight = (NetLearningRate * n-е выходное значение * n-й градиент + импульс * OldDeltaWeight). Затем назначьте новый вес как (OldWeight + NewDeltaWeight)
- Повторите процесс.
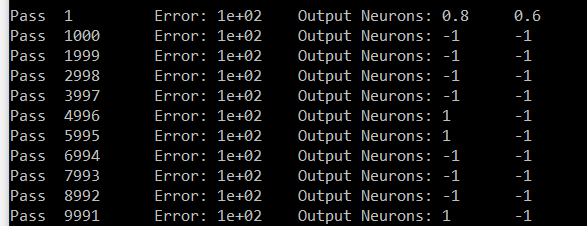
Вот моя попытка получить цифру семь. Выходными данными являются Нейрон № 0 и Нейрон № 6. Нейрон № 6 должен нести 1, а Нейрон № 0 должен нести 0. В моих результатах все Нейрон, кроме шести, имеют одинаковое значение (№ ноль - образец).
Простите за длинный пост. Если вы знаете это, то, вероятно, знаете, как это круто и насколько важно быть в одном посте. заранее спасибо
1 ответ
Softmax с log-loss обычно используется для функции активации выходного уровня мультикласса. У вас есть мультикласс / мультиномиал: с 10 возможными цифрами, составляющими 10 классов.
Так что вы можете попробовать изменить функцию активации выходного слоя на softmax
http://en.wikipedia.org/wiki/Softmax_function
Искусственные нейронные сети
При моделировании нейронной сети функция softmax часто реализуется на последнем уровне сети, используемой для классификации. Такие сети затем обучаются в режиме потерь (или кросс-энтропии), что дает нелинейный вариант полиномиальной логистической регрессии.
Дайте нам знать, какой эффект это имеет. -