Генерация матрицы, содержащей все комбинации элементов, взятых из n векторов
Этот вопрос всплывает довольно часто в той или иной форме (см., Например, здесь или здесь). Поэтому я решил представить его в общем виде и дать ответ, который мог бы послужить для дальнейшего использования.
Дано произвольное число
nвекторов возможно разных размеров, генерироватьnматрица из столбцов, строки которой описывают все комбинации элементов, взятых из этих векторов (декартово произведение).
Например,
vectors = { [1 2], [3 6 9], [10 20] }
должен дать
combs = [ 1 3 10
1 3 20
1 6 10
1 6 20
1 9 10
1 9 20
2 3 10
2 3 20
2 6 10
2 6 20
2 9 10
2 9 20 ]
4 ответа
ndgrid Функция почти дает ответ, но имеет одно предупреждение: n выходные переменные должны быть явно определены для вызова. поскольку n произвольно, лучше всего использовать разделенный запятыми список (генерируемый из массива ячеек с n клетки), чтобы служить выходом. Результирующий n Матрицы затем объединяются в желаемый n матрица
vectors = { [1 2], [3 6 9], [10 20] }; %// input data: cell array of vectors
n = numel(vectors); %// number of vectors
combs = cell(1,n); %// pre-define to generate comma-separated list
[combs{end:-1:1}] = ndgrid(vectors{end:-1:1}); %// the reverse order in these two
%// comma-separated lists is needed to produce the rows of the result matrix in
%// lexicographical order
combs = cat(n+1, combs{:}); %// concat the n n-dim arrays along dimension n+1
combs = reshape(combs,[],n); %// reshape to obtain desired matrix
Немного проще... если у вас есть набор инструментов Neural Network, вы можете просто использовать combvec:
vectors = {[1 2], [3 6 9], [10 20]};
combs = combvec(vectors{:}).' % Use cells as arguments
который возвращает матрицу в несколько ином порядке:
combs =
1 3 10
2 3 10
1 6 10
2 6 10
1 9 10
2 9 10
1 3 20
2 3 20
1 6 20
2 6 20
1 9 20
2 9 20
Если вы хотите матрицу, которая находится в вопросе, вы можете использовать sortrows:
combs = sortrows(combvec(vectors{:}).')
% Or equivalently as per @LuisMendo in the comments:
% combs = fliplr(combvec(vectors{end:-1:1}).')
который дает
combs =
1 3 10
1 3 20
1 6 10
1 6 20
1 9 10
1 9 20
2 3 10
2 3 20
2 6 10
2 6 20
2 9 10
2 9 20
Если вы посмотрите на внутренности combvec (тип edit combvec в командном окне) вы увидите, что он использует код, отличный от ответа @LuisMendo. Я не могу сказать, что является более эффективным в целом.
Если у вас есть матрица, строки которой похожи на ранний массив ячеек, вы можете использовать:
vectors = [1 2;3 6;10 20];
vectors = num2cell(vectors,2);
combs = sortrows(combvec(vectors{:}).')
Я провел сравнительный анализ двух предложенных решений. Код сравнительного анализа основан на timeit функция, и включена в конце этого поста.
Я рассматриваю два случая: три вектора размера nи три вектора размеров n/10, n а также n*10 соответственно (оба случая дают одинаковое количество комбинаций). n варьируется до максимума 240 (Я выбираю это значение, чтобы избежать использования виртуальной памяти на моем ноутбуке).
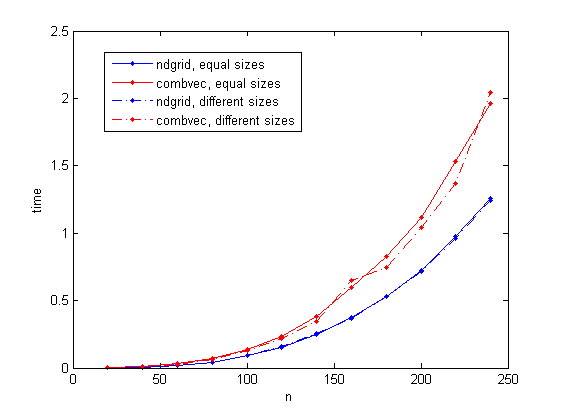
Результаты приведены на следующем рисунке. ndgridрешение, как видно, последовательно занимает меньше времени, чем combvec, Также интересно отметить, что время, затрачиваемое combvec меняется немного реже в случае разного размера.
Код бенчмаркинга
Функция для ndgridрешение на основе:
function combs = f1(vectors)
n = numel(vectors); %// number of vectors
combs = cell(1,n); %// pre-define to generate comma-separated list
[combs{end:-1:1}] = ndgrid(vectors{end:-1:1}); %// the reverse order in these two
%// comma-separated lists is needed to produce the rows of the result matrix in
%// lexicographical order
combs = cat(n+1, combs{:}); %// concat the n n-dim arrays along dimension n+1
combs = reshape(combs,[],n);
Функция для combvec решение:
function combs = f2(vectors)
combs = combvec(vectors{:}).';
Скрипт для измерения времени по телефону timeit на эти функции:
nn = 20:20:240;
t1 = [];
t2 = [];
for n = nn;
%//vectors = {1:n, 1:n, 1:n};
vectors = {1:n/10, 1:n, 1:n*10};
t = timeit(@() f1(vectors));
t1 = [t1; t];
t = timeit(@() f2(vectors));
t2 = [t2; t];
end
Вот метод "сделай сам", который заставил меня хихикать от восторга, используя nchoosek, хотя это не лучше, чем принятое решение @Luis Mendo.
Для приведенного примера, после 1000 прогонов это решение заняло у моей машины в среднем 0,00065935 с, а принятое решение - 0,00012877 с. Для больших векторов, следуя посту @Luis Mendo, это решение медленнее, чем принятый ответ. Тем не менее, я решил опубликовать это в надежде, что, возможно, вы найдете что-то полезное об этом:
Код:
tic;
v = {[1 2], [3 6 9], [10 20]};
L = [0 cumsum(cellfun(@length,v))];
V = cell2mat(v);
J = nchoosek(1:L(end),length(v));
J(any(J>repmat(L(2:end),[size(J,1) 1]),2) | ...
any(J<=repmat(L(1:end-1),[size(J,1) 1]),2),:) = [];
V(J)
toc
дает
ans =
1 3 10
1 3 20
1 6 10
1 6 20
1 9 10
1 9 20
2 3 10
2 3 20
2 6 10
2 6 20
2 9 10
2 9 20
Elapsed time is 0.018434 seconds.
Объяснение:
L получает длины каждого вектора, используя cellfun, Хотя cellfun это в основном цикл, здесь он эффективен, учитывая, что число векторов должно быть относительно низким, чтобы эта проблема была даже практичной.
V объединяет все векторы для легкого доступа позже (предполагается, что вы ввели все свои векторы как строки. v'будет работать для векторов столбцов.)
nchoosek получает все способы выбрать n=length(v) элементы из общего количества элементов L(end), Здесь будет больше комбинаций, чем нам нужно.
J =
1 2 3
1 2 4
1 2 5
1 2 6
1 2 7
1 3 4
1 3 5
1 3 6
1 3 7
1 4 5
1 4 6
1 4 7
1 5 6
1 5 7
1 6 7
2 3 4
2 3 5
2 3 6
2 3 7
2 4 5
2 4 6
2 4 7
2 5 6
2 5 7
2 6 7
3 4 5
3 4 6
3 4 7
3 5 6
3 5 7
3 6 7
4 5 6
4 5 7
4 6 7
5 6 7
Поскольку есть только два элемента в v(1)нам нужно выбросить любые строки где J(:,1)>2, Точно так же, где J(:,2)<3, J(:,2)>5и т.д... Использование L а также repmat мы можем определить, является ли каждый элемент J находится в соответствующем диапазоне, а затем использовать any отбросить строки, которые имеют какой-либо плохой элемент.
Наконец, это не фактические значения из vПросто индексы. V(J) вернет желаемую матрицу.