Самый быстрый способ определить, находится ли целое число между двумя целыми числами (включительно) с известными наборами значений
Есть ли более быстрый способ, чем x >= start && x <= end в C или C++, чтобы проверить, если целое число находится между двумя целыми числами?
ОБНОВЛЕНИЕ: Моя конкретная платформа - iOS. Это часть функции размытия рамки, которая ограничивает пиксели кругом в данном квадрате.
ОБНОВЛЕНИЕ: Попробовав принятый ответ, я получил ускорение на порядок на одну строку кода по сравнению с обычным x >= start && x <= end путь.
ОБНОВЛЕНИЕ: Вот код после и до с ассемблером из XCode:
НОВЫЙ СПОСОБ
// diff = (end - start) + 1
#define POINT_IN_RANGE_AND_INCREMENT(p, range) ((p++ - range.start) < range.diff)
Ltmp1313:
ldr r0, [sp, #176] @ 4-byte Reload
ldr r1, [sp, #164] @ 4-byte Reload
ldr r0, [r0]
ldr r1, [r1]
sub.w r0, r9, r0
cmp r0, r1
blo LBB44_30
СТАРЫЙ ПУТЬ
#define POINT_IN_RANGE_AND_INCREMENT(p, range) (p <= range.end && p++ >= range.start)
Ltmp1301:
ldr r1, [sp, #172] @ 4-byte Reload
ldr r1, [r1]
cmp r0, r1
bls LBB44_32
mov r6, r0
b LBB44_33
LBB44_32:
ldr r1, [sp, #188] @ 4-byte Reload
adds r6, r0, #1
Ltmp1302:
ldr r1, [r1]
cmp r0, r1
bhs LBB44_36
Довольно удивительно, как сокращение или устранение ветвления может обеспечить такое резкое ускорение.
7 ответов
Есть старый трюк, чтобы сделать это только с одним сравнением / ответвлением. Может ли это действительно улучшить скорость, может быть под вопросом, и даже если это произойдет, это, вероятно, слишком мало, чтобы заметить или позаботиться о нем, но когда вы только начинаете с двух сравнений, шансы на огромное улучшение довольно малы. Код выглядит так:
// use a < for an inclusive lower bound and exclusive upper bound
// use <= for an inclusive lower bound and inclusive upper bound
// alternatively, if the upper bound is inclusive and you can pre-calculate
// upper-lower, simply add + 1 to upper-lower and use the < operator.
if ((unsigned)(number-lower) <= (upper-lower))
in_range(number);
В типичном современном компьютере (то есть, в любом, использующем дополнение по два) преобразование в unsigned на самом деле не имеет значения - просто изменение в том, как рассматриваются те же самые биты.
Обратите внимание, что в типичном случае вы можете предварительно вычислить upper-lower вне (предполагаемого) цикла, так что обычно оно не дает значительного времени. Наряду с уменьшением количества команд ветвления это также (как правило) улучшает предсказание ветвления. В этом случае одна и та же ветвь берется независимо от того, находится число ниже нижнего конца или выше верхнего конца диапазона.
Что касается того, как это работает, основная идея довольно проста: отрицательное число, если рассматривать его как число без знака, будет больше, чем все, что начиналось как положительное число.
На практике этот метод переводит number и интервал до места происхождения и проверяет, если number находится в интервале [0, D], где D = upper - lower, Если number ниже нижней границы: отрицательный, а если выше верхней границы: больше чемD,
Редко можно сделать существенную оптимизацию для кода в таком маленьком масштабе. Большой выигрыш в производительности достигается за счет наблюдения и изменения кода на более высоком уровне. Вы можете полностью исключить необходимость проверки диапазона или выполнить только O(n) вместо O(n^2). Возможно, вам удастся изменить порядок тестов, чтобы всегда подразумевалась одна сторона неравенства. Даже если алгоритм идеален, выигрыш будет более вероятен, когда вы увидите, как этот код выполняет тестирование диапазона 10 миллионов раз, и вы найдете способ их пакетировать и использовать SSE для параллельного выполнения множества тестов.
Это зависит от того, сколько раз вы хотите выполнить тест на одних и тех же данных.
Если вы выполняете тест один раз, вероятно, нет никакого существенного способа ускорить алгоритм.
Если вы делаете это для очень ограниченного набора значений, то вы можете создать справочную таблицу. Выполнение индексации может быть более дорогим, но если вы можете разместить всю таблицу в кеше, тогда вы можете удалить все ветвления из кода, что должно ускорить процесс.
Для ваших данных таблица поиска будет 128^3 = 2 097 152. Если вы можете контролировать одну из трех переменных, то вы должны рассмотреть все случаи, когда start = N за один раз размер рабочего набора уменьшается до 128^2 = 16432 байты, которые должны хорошо вписываться в большинство современных кэшей.
Вам все равно придется сравнить реальный код, чтобы увидеть, является ли таблица поиска без ответвлений достаточно быстрой, чем очевидные сравнения.
Для любой проверки диапазона переменных:
if (x >= minx && x <= maxx) ...
Быстрее использовать битовую операцию:
if ( ((x - minx) | (maxx - x)) >= 0) ...
Это сократит две ветки в одну.
Если вы заботитесь о безопасном типе:
if ((int32_t)(((uint32_t)x - (uint32_t)minx) | ((uint32_t)maxx - (uint32_t)x)) > = 0) ...
Вы можете объединить больше проверок диапазона переменных вместе:
if (( (x - minx) | (maxx - x) | (y - miny) | (maxy - y) ) >= 0) ...
Это сократит 4 ветки до 1.
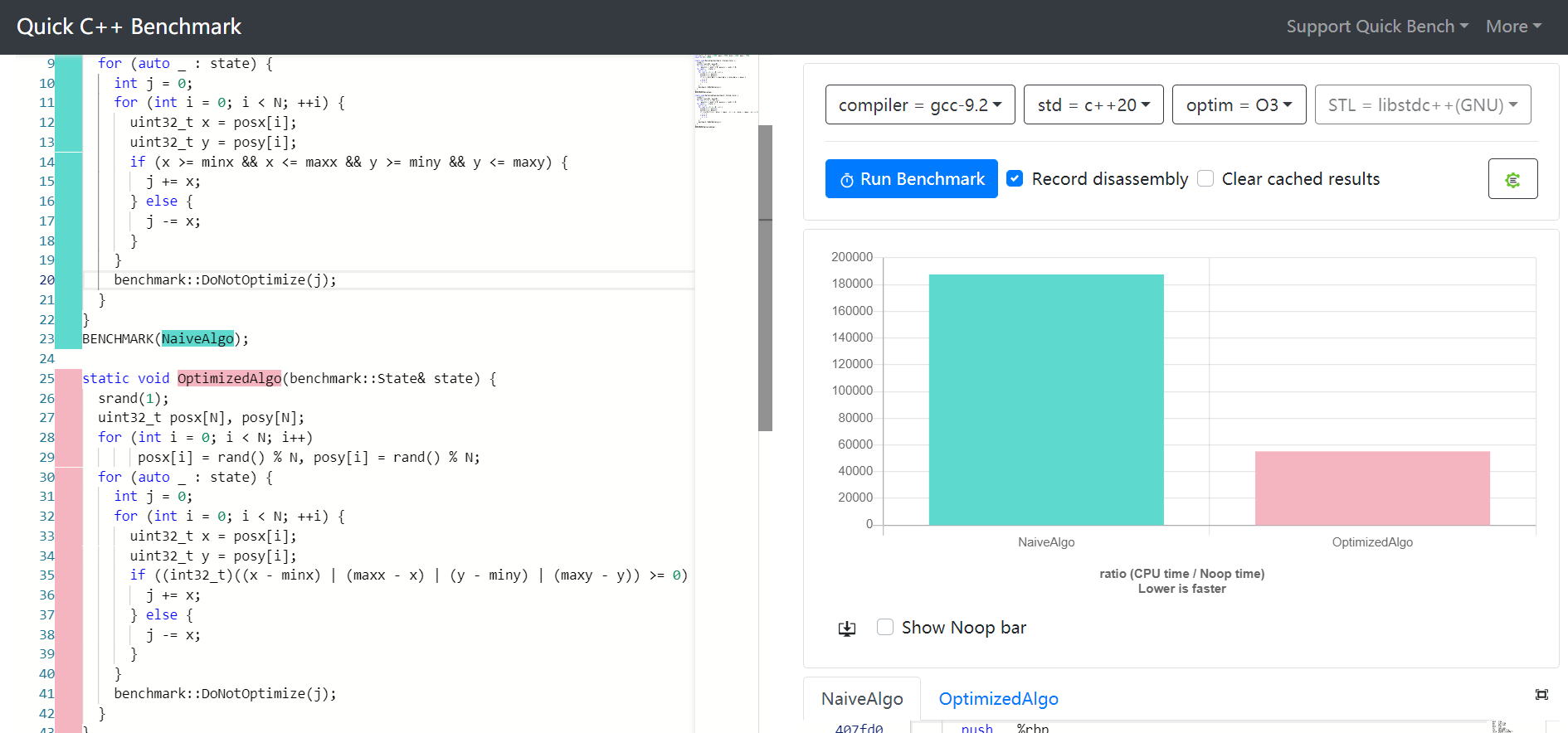
Он в 3,4 раза быстрее старого в gcc:
Этот ответ должен сообщить о тестировании, выполненном с принятым ответом. Я выполнил тест с закрытым диапазоном для большого вектора отсортированного случайного целого числа, и, к моему удивлению, основной метод ( low <= num && num <= high) фактически быстрее, чем принятый ответ выше! Тест проводился на HP Pavilion g6 (AMD A6-3400APU с оперативной памятью 6 ГБ. Вот основной код, использованный для тестирования:
int num = rand(); // num to compare in consecutive ranges.
chrono::time_point<chrono::system_clock> start, end;
auto start = chrono::system_clock::now();
int inBetween1{ 0 };
for (int i = 1; i < MaxNum; ++i)
{
if (randVec[i - 1] <= num && num <= randVec[i])
++inBetween1;
}
auto end = chrono::system_clock::now();
chrono::duration<double> elapsed_s1 = end - start;
по сравнению со следующим, который является принятым ответом выше:
int inBetween2{ 0 };
for (int i = 1; i < MaxNum; ++i)
{
if (static_cast<unsigned>(num - randVec[i - 1]) <= (randVec[i] - randVec[i - 1]))
++inBetween2;
}
Обратите внимание, что randVec является отсортированным вектором. Для любого размера MaxNum первый метод превосходит второй на моей машине!
Я могу точно сказать, почему это имеет значение. Представьте, что вы моделируете MMU. Вы постоянно должны убедиться, что данный адрес памяти существует с данным набором страниц. Эти маленькие кусочки складываются очень быстро, потому что вы всегда говорите
- Этот адрес действителен?
- На какой странице находится этот адрес?
- Какие права у этой страницы?
Разве нельзя просто выполнить побитовую операцию над целым числом?
Так как он должен быть между 0 и 128, если установлен 8-й бит (2^7), он равен 128 или более. Тем не менее, крайний случай будет болезненным, так как вы хотите получить инклюзивное сравнение.