Квантовые вычисления и шифрование
Некоторое время назад я читал, что Quantum Computers может за короткое время прервать большинство типов хеширования и шифрования, используемых сегодня (я полагаю, это были просто минуты). Как это возможно? Я пытался читать статьи об этом, но я теряюсь в a quantum bit can be 1, 0, or something else, Может кто-нибудь объяснить, как это относится к взлому таких алгоритмов на простом английском языке без всякой изворотливой математики?
10 ответов
Преамбула: Квантовые компьютеры - странные звери, которых мы действительно еще не приручили до такой степени, что они полезны. Теория, лежащая в их основе, абстрактна и математична, поэтому любое обсуждение того, как они могут быть более эффективными, чем классические компьютеры, неизбежно будет долгим и сложным. Вам понадобится хотя бы базовое понимание линейной алгебры и квантовой механики, чтобы понять детали, но я постараюсь передать мое ограниченное понимание!
Основная предпосылка квантовых вычислений - квантовая суперпозиция. Идея состоит в том, что квантовая система (такая как квантовый бит или кубит, квантовый аналог нормального бита) может, как вы говорите, существовать не только в 0 а также 1 состояния (называемые вычислительными базовыми состояниями системы), но также и в любой комбинации двух (так что каждый имеет амплитуду, связанную с ним). Когда кто-то наблюдает за системой, состояние кубита коллапсирует в одно из его базовых состояний (возможно, вы слышали об мысленном эксперименте Шредингера с кошкой, который связан с этим).
Из-за этого, реестр n кубиты имеет 2^n свои собственные базовые состояния (это состояния, в которых вы могли наблюдать регистр; представьте классическое n-битное целое число). Поскольку регистр может существовать в суперпозиции всех этих состояний одновременно, можно применять вычисления ко всем 2^n регистрировать состояния, а не только один из них. Это называется квантовым параллелизмом.
Из-за этого свойства квантовых компьютеров может показаться, что это серебряная пуля, которая может решить любую проблему в геометрической прогрессии быстрее, чем классический компьютер. Но это не так просто: проблема в том, что, как только вы наблюдаете результат ваших вычислений, он (как я уже упоминал выше) превращается в результат только одного из вычислений - и вы теряете все остальные.
Область квантовых вычислений / алгоритмов - это попытка обойти эту проблему, манипулируя квантовыми явлениями для извлечения информации за меньшее количество операций, чем это было бы возможно на классическом компьютере. Оказывается, очень трудно придумать "квантовый алгоритм", который быстрее любого возможного классического аналога.
Пример, о котором вы спрашиваете, - это квантовый криптоанализ. Предполагается, что квантовые компьютеры могут "взломать" определенные алгоритмы шифрования: в частности, алгоритм RSA, который основан на трудности определения основных факторов очень больших целых чисел. Алгоритм, который учитывает это, называется алгоритмом Шора, который может вычислять целые числа с полиномиальной временной сложностью. В отличие от этого лучший классический алгоритм для задачи имеет (почти) экспоненциальную временную сложность, и, следовательно, проблема считается " неразрешимой".
Если вы хотите глубже понять это, приобретите несколько книг по линейной алгебре и квантовой механике и почувствуйте себя комфортно. Если вам нужны пояснения, я посмотрю, что я могу сделать!
В сторону: чтобы лучше понять идею квантовой суперпозиции, подумайте о вероятностях. Представьте, что вы подбрасываете монету и ловите ее на своей руке, прикрытой так, что вы ее не видите. В качестве очень сомнительной аналогии монета может рассматриваться как находящаяся в суперпозиции "состояний" голов и хвостов: каждое имеет вероятность 0,5 (и, естественно, поскольку существует два состояния, эти вероятности составляют в целом 1).). Когда вы убираете руку и наблюдаете за монетой непосредственно, она падает в состояние либо головы, либо хвоста, и поэтому вероятность этого состояния становится равной 1, а другой - 0. Один способ думать об этом, я полагаю, это набор шкал, который сбалансирован до наблюдения, и в этот момент он падает в сторону, когда наши знания о системе увеличиваются, и одно состояние становится "реальным" состоянием.
Конечно, мы не думаем о монете как о квантовой системе: для всех практических целей у монеты есть определенное состояние, даже если мы ее не видим. Однако для подлинных квантовых систем (таких как отдельная частица, попавшая в коробку) мы не можем думать об этом таким образом. Согласно традиционной интерпретации квантовой механики, частица принципиально не имеет определенного положения, но существует во всех возможных положениях одновременно. Только при наблюдении его положение ограничено в пространстве (хотя только в ограниченной степени; см. Принцип неопределенности), и даже это является чисто случайным и определяется только вероятностью.
Кстати, квантовые системы не ограничиваются наличием только двух наблюдаемых состояний (так называемые двухуровневые системы). Некоторые имеют большое, но конечное число, некоторые имеют счетное бесконечное число (например, "частица в коробке" или гармонический осциллятор), а некоторые даже имеют бесконечно бесконечное число (например, положение свободной частицы, которое не не ограничены отдельными точками в пространстве).
Статья в Википедии очень хорошо объясняет это.
Короче говоря, если у вас N битов, ваш квантовый компьютер может одновременно находиться в 2^N состояниях. Концептуально аналогично обработке 2^N ЦП с традиционными битами (хотя не совсем так).
Это очень теоретически на данный момент. Квантовые биты могут предложить возможность взломать шифрование, но, очевидно, это еще не все.
На квантовом уровне законы, управляющие поведением, отличаются от макроуровня.
Чтобы ответить на ваш вопрос, сначала нужно понять, как работает шифрование.
На базовом уровне шифрование является результатом умножения двух чрезвычайно больших простых чисел вместе. Этот сверхбольший результат делится на 1 и на эти два простых числа.
Один из способов сломать шифрование состоит в том, чтобы с помощью грубой силы угадать два простых числа, выполняя факторизацию простого числа.
Эта атака медленная, и ей мешают выбирать все больше и больше простых чисел. Вы слышите о размерах ключа 40 бит,56 бит,128 бит, а теперь 256,512 бит и выше. Эти размеры соответствуют размеру числа.
Алгоритм перебора (в упрощенном виде) может выглядеть
for(int i = 3; i < int64.max; i++)
{
if( key / i is integral)
{
//we have a prime factor
}
}
Итак, вы хотите грубой силой попробовать простые числа; хорошо, что это займет некоторое время с одним компьютером. Так что вы можете попробовать сгруппировать кучу компьютеров, чтобы разделить и победить. Это работает, но все еще медленно для очень больших ключей.
Как квантово-битовый адрес это то, что они оба равны 0 и 1 одновременно. Итак, скажем, у вас есть 3 квантовых бита (не маленький подвиг, заметьте)
С 3 кубитами ваша программа может одновременно иметь значения 0-7
(000,001,010,011 и т. Д.)
, который включает в себя простые числа 3,5,7 одновременно.
поэтому, используя простой алгоритм, приведенный выше, вместо увеличения i на 1 каждый раз, вы можете просто разделить один раз и проверить
0,1,2,3,4,5,6,7
Все одновременно.
Конечно, квантовые биты еще не до этого момента; предстоит еще много работы на местах; но это должно дать вам представление о том, что если бы мы могли программировать с использованием квантов, как мы могли бы взломать шифрование.
Почти все наши шифрования с открытым ключом (например, RSA) основаны исключительно на математике, полагаясь на сложность факторизации или дискретных логарифмов. Оба из них будут эффективно сломаны с использованием квантовых компьютеров (хотя даже после бакалавриата по CS и математике и после прохождения нескольких классов по квантовой механике я до сих пор не понимаю алгоритм).
Однако алгоритмы хеширования (например, SHA2) и шифрования с симметричным ключом (например, AES), которые основаны главным образом на распространении и путанице, по-прежнему безопасны.
Квантовый компьютер может реализовать алгоритм Шора, который может быстро выполнить простую факторизацию. Системы шифрования построены на предположении, что большие числа не могут быть учтены в разумные сроки на классическом компьютере.
квантовые компьютеры и т. д. все ложь. Я не верю этим научно-фантастическим журналам. на самом деле система rsa основана на двух простых числах и их умножении. p1,p2 - огромные простые числа p1xp2=N модуль. rsa система подобна тому, что выбирают простое число.. может быть маленьким его открытый ключ E (p1-1)*(p2-1)=R найти число D, которое делает E*D=1 mod(R), которым мы делимся (E,N) данные как открытый ключ, публично мы надежно сохраняем (D,N) как частный.
Чтобы решить эту задачу, взломщику системы Rsa нужно найти простые множители N. * масса Вселенной ближе к 10^53 кг * масса электрона равна 9.10938291 × 10^-31 килограмм, если разделить вселенную на электроны, мы можем создать 10^84 электронов, электроны имеют более медленные скорости, чем свет. частота его движения может составлять 10^26, если кто-нибудь производит параллельные rsa первичные множители размера электрона из всей массы вселенной. вся вселенная может обрабатывать (10^84)*(10^26)= 10^110 чисел в секунду.
rsa имеет лимиты битов альтернативных простых чисел. может быть 4096 бит 4096 бит RSA имеет 10 600 возможных простых чисел для грубой силы. так что ваш квантовый решатель Вселенной должен сделать тесты в течение 10 500 лет.
rsa vs вселенная масса квантовый компьютер 1 - 0
возможно, квантовый компьютер может взломать пароли 64/128 бит. потому что 128-битный пароль имеет 10^39 возможных узлов перебора.
Еще более странный ИМО. алгоритм Гровера В качестве входных данных мы получаем несортированный массив целых чисел с arraylength = n. Каково ожидаемое время выполнения алгоритма, который находит минимальное значение этого массива? Ну, классически мы должны хотя бы проверить каждый элемент массива 1..n, что приведет к ожидаемому времени выполнения n. Для квантовых компьютеров это не так, на квантовом компьютере мы можем решить это в ожидаемом времени выполнения с максимальным root(n), это означает, что нам даже не нужно проверять каждый элемент, чтобы найти гарантированное решение...
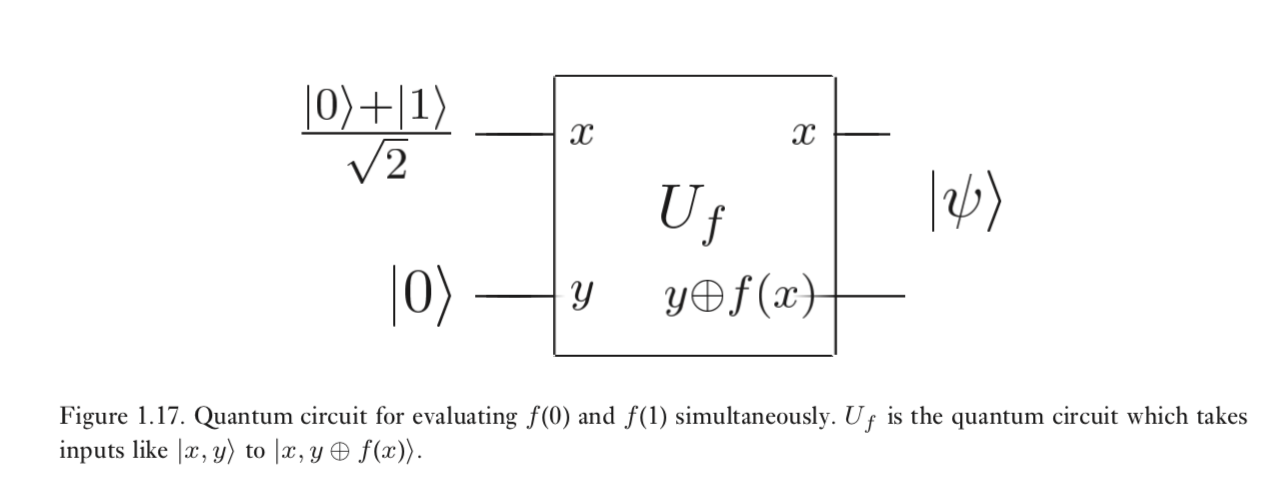
Эта схема - хорошее начало, чтобы понять, как работает параллельный кубит. Вход 2-кубитов находится слева. Верхний кубит равен x, а нижний - y. Кубит y на входе равен 0, как обычный бит. Х-кубит, с другой стороны, находится в суперпозиции на входе. y (+) f(x) означает здесь сложение по модулю 2, что означает 1+1=0, 0+1=1+0=1. Но интересная часть заключается в том, что, поскольку x-кубит находится в суперпозиции, f(x) - это f(0) и f(1) одновременно, и мы можем выполнить оценку функции f для всех состояний одновременно, не используя какие-либо (отнимает много времени) петли. Имея достаточно пристрастий, мы можем разветвлять это на бесконечно усложняющие движения.
Во-первых, квантовые вычисления все еще находятся за пределами теоретической стадии. Происходит много исследований и экспериментальных квантовых ячеек и цепей, но "квантового компьютера" еще не существует.
Во-вторых, прочитайте статью в Википедии: http://en.wikipedia.org/wiki/Quantum_computer
В частности, "в общем случае квантовый компьютер с n кубитами может находиться в произвольной суперпозиции до 2^n различных состояний одновременно (это сравнивается с нормальным компьютером, который может находиться только в одном из этих 2^n состояний одновременно".). "
Что делает криптографию защищенной, так это использование ключей шифрования с очень длинными числами, для которых потребуется очень и очень много времени, чтобы учесть их составляющие простые числа, а ключи достаточно длинные, чтобы грубая сила попыталась попробовать каждое возможное значение ключа. также займет слишком много времени, чтобы завершить.
Поскольку квантовые вычисления могут (теоретически) представлять множество состояний в небольшом количестве ячеек-кубитов и одновременно работать со всеми этими состояниями, представляется, что существует возможность использовать квантовые вычисления для выполнения "грубой силы", пытаясь сделать все возможное - значения ключа в очень короткий промежуток времени.
Если такая вещь возможна, это может быть конец криптографии, как мы ее знаем.
В самых основных терминах обычный не квантовый компьютер работает, работая с битами (состояниями включения или выключения), используя булеву логику. Вы делаете это очень быстро для большого и большого количества битов, и вы можете решить любую проблему в классе задач, которые вычислимы.
Однако это "ограничения скорости", а именно то, что называется вычислительной сложностью. Это в терминах непрофессионала означает, что для данного алгоритма вы знаете, что время, необходимое для запуска алгоритма (и пространство памяти, необходимое для запуска алгоритма), имеет минимальную границу, Например, алгоритм O(n^2) означает, что для размера данных n потребуется n ^ 2 времени для запуска.
Однако этот вид выходит из окна, когда у нас есть кубиты (квантовые биты), когда вы выполняете операции над кубитами, которые могут иметь значения "между". Алгоритмы, которые будут иметь очень высокую вычислительную сложность (такие как факторинг огромных чисел, ключ к взлому многих алгоритмов шифрования), могут быть выполнены с гораздо меньшей вычислительной сложностью. Это причина того, что квантовые вычисления смогут взламывать зашифрованные потоки на порядки быстрее, чем обычные компьютеры.