Использование пуассоновской структуры ошибок в нелинейном подборе

Question

Я установил трилинейную модель

library(nlstools)
library(nlsMicrobio)
library(investr) # for plotFit function
trilinear
LOG10N ~ LOG10N0 - (t >= Sl) * (t <= (Sl + (LOG10N0 - LOG10Nres) * 
    log(10)/kmax)) * kmax * (t - Sl)/log(10) + (t >= Sl) * (t > 
    (Sl + (LOG10N0 - LOG10Nres) * log(10)/kmax)) * (LOG10Nres - 
    LOG10N0)

к данным бактериальной выживаемости

data(survivalcurve1)
survivalcurve1
       t LOG10N
1   0.00   7.56
2   0.33   7.41
3   1.00   7.26
4   2.00   7.30
5   3.00   7.26
6   4.00   7.15
7   5.00   7.30
8   6.00   6.48
9   7.00   6.15
10  8.00   5.30
11  9.00   4.78
12 10.00   5.11
13 11.00   2.30
14 13.00   3.15
15 14.00   2.00
16 16.00   1.00
17 18.00   1.00
18 20.00   1.00
19 23.00   1.00

используя OLS в сочетании с nls:

nls = nls(trilinear, survivalcurve1,
           list(Sl = 5, kmax = 1.5, LOG10N0 = 7, LOG10Nres = 1))
overview(nls)
Parameters:
          Estimate Std. Error t value Pr(>|t|)    
Sl          4.7064     0.5946   7.915 9.82e-07 ***
kmax        1.3223     0.1222  10.818 1.76e-08 ***
LOG10N0     7.3233     0.1884  38.875  < 2e-16 ***
LOG10Nres   1.0000     0.2307   4.334  0.00059 ***
t-based confidence interval:
               2.5%    97.5%
Sl        3.4389618 5.973874
kmax      1.0617863 1.582868
LOG10N0   6.9218035 7.724863
LOG10Nres 0.5082284 1.491772

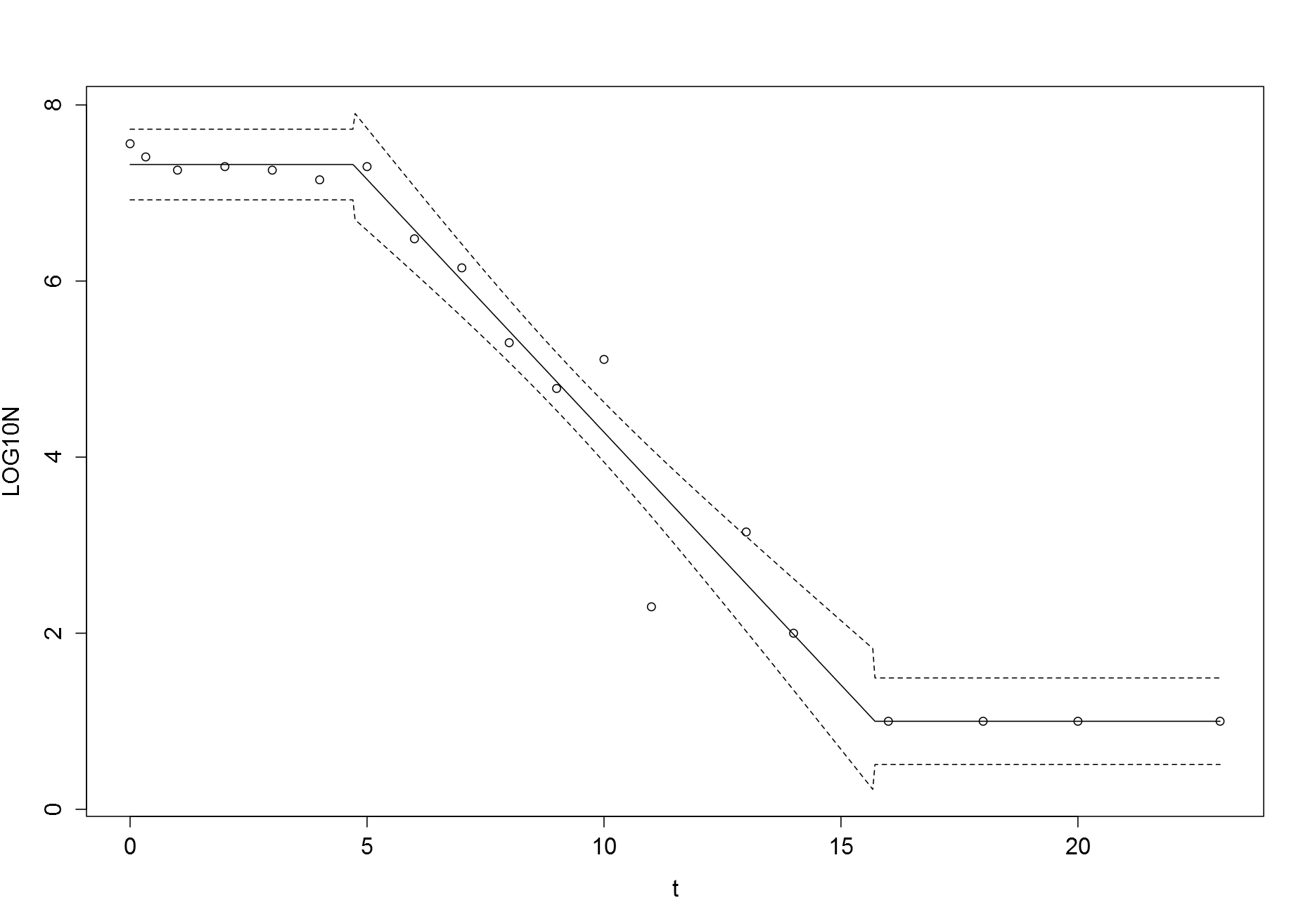
plotFit(nls, interval="confidence")

Мне было интересно, если бы я мог также соответствовать этой модели, используя максимальную вероятность для исходных (не логарифмированных) ячеек NRS (который будет в этом случае survivalcurve1$N = (10^survivalcurve1$LOG10N)), принимая во внимание, что структура ошибки будет приблизительно Пуассона? Может быть, это может быть сделано с помощью bbmle"s mle2и если так, какой будет правильный синтаксис?

РЕДАКТИРОВАТЬ: я пытался с

survivalcurve1$N = as.integer(10^survivalcurve1$LOG10N)
trilinearN=formula(N ~ dpois( 10^(LOG10N0 - (t >= Sl) * (t <= (Sl + (LOG10N0 - LOG10Nres) * 
log(10)/kmax)) * kmax * (t - Sl)/log(10) + (t >= Sl) * (t > (Sl + (LOG10N0 - LOG10Nres) * log(10)/kmax)) * (LOG10Nres - LOG10N0))))
m1 = mle2(trilinearN,  start=list(Sl = 5, kmax = 1.5, LOG10N0 = 7, LOG10Nres = 1), data=survivalcurve1)

а также

coef(summary(m1))

дает мне

           Estimate   Std. Error       z value Pr(z)
Sl         4.902048 1.669354e-04  2.936495e+04     0
kmax       1.475309 3.210865e-04  4.594739e+03     0
LOG10N0    7.344014 3.785883e-05  1.939842e+05     0
LOG10Nres -1.830498 1.343019e-10 -1.362972e+10     0

Не удалось заставить работать прогнозы:

df=data.frame(t=seq(0,max(survivalcurve1$t),length=100))
df$pred=predict(m1,newdata=df)
with(df,lines(t,pred,col=2))

как это дало мне ошибку

Error : object of type 'symbol' is not subsettable
Error in gfun(object, newdata = newdata, location = location, op = "predict") : 
  can only use predict() if formula specified

Какие-нибудь мысли? Кроме того, как бы я разобрать, если Пуассон mle2 подходит лучше, чем nls один? (Поскольку AIC нельзя сравнивать из-за разницы в масштабе)

PS The geeraerd модель тоже подойдет, если будет проще:

geeraerd
LOG10N ~ LOG10Nres + log10((10^(LOG10N0 - LOG10Nres) - 1) * exp(kmax * 
    Sl)/(exp(kmax * t) + (exp(kmax * Sl) - 1)) + 1)