Различия между результатами DFT и FFT (величина)

Question

Я стремлюсь получить DFT изображения в OpenCV.

С помощью dft Функция, я могу рассчитать его, а затем раскрасить его, рассчитав его величину (затем примените журнал и, наконец, нормализуйте его, чтобы нарисовать значения между 0 и 1).

Мой результат для следующего изображения - это результат, который я вам показываю (с перестановкой, чтобы иметь более низкие частоты в центре изображения):

Тем не менее, если я сравниваю его с результатом, полученным с помощью других инструментов, таких как Halcon, он кажется мне некорректным, поскольку он имеет действительно "высокие" значения (я имею в виду величину DFT OpenCV):

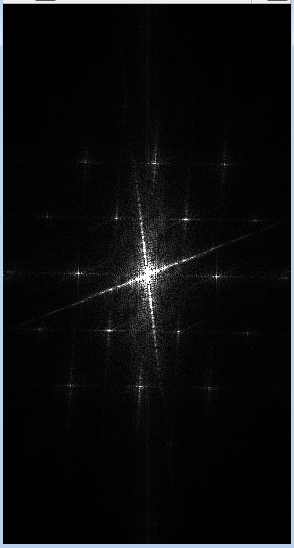
Я думал, что это может быть по этим причинам:

1. Разница между DFT (в OpenCV) и FFT (Halcon)
2. Операции, которые я выполняю , чтобы показать величину в OpenCV.

Первая проблема связана с тем, что мне довольно сложно анализировать, и OpenCV не имеет функции FFT, а также Halcon не имеет функции DFT (если я, конечно, не ошибаюсь), так что я могу не сравнивайте это напрямую.

Второй, в котором я работаю больше всего времени, но я до сих пор не могу найти причину, если он там есть.

Там код, который я использую, чтобы нарисовать величину img (это мое изображение DFT):

// 1.- To split the image in Re | Im values
Mat planes[] = {Mat_<float>(img), Mat::zeros(img.size(), CV_32F)};

// 2.- To magnitude + phase
split(img, planes);

// Calculate magnitude. I overwrite it, I know, but this is inside a function so it will be never used again, doesn't matter
magnitude(planes[0], planes[1], planes[0]);

// Magnitude Mat
Mat magI = planes[0];

// 3.- We add 1 to all them in order to perform the log
magI += Scalar::all(1);                    // switch to logarithmic scale
log(magI, magI);

// 4.- Swap the quadrants to center frequency
magI = magI(Rect(0, 0, magI.cols & -2, magI.rows & -2));
int cx = magI.cols/2;
int cy = magI.rows/2;

Mat q0(magI, Rect(0, 0, cx, cy));   // Top-Left - Create a ROI per quadrant
Mat q1(magI, Rect(cx, 0, cx, cy));  // Top-Right
Mat q2(magI, Rect(0, cy, cx, cy));  // Bottom-Left
Mat q3(magI, Rect(cx, cy, cx, cy)); // Bottom-Right

// swap quadrants (Top-Left with Bottom-Right)
Mat tmp;
q0.copyTo(tmp);
q3.copyTo(q0);
tmp.copyTo(q3);

// swap quadrant (Top-Right with Bottom-Left)
q1.copyTo(tmp);
q2.copyTo(q1);
tmp.copyTo(q2);

// 5.- Normalize
// Transform the matrix with float values into a
// viewable image form (float between values 0 and 1).
normalize(magI, magI, 0, 1, CV_MINMAX); 

// Paint it
imshow( "Magnitud DFT", magI);

Итак, подведем итог: есть идеи о том, почему у меня такая разница между этими двумя величинами?

Answer 1

Я суммирую мои комментарии в ответ.

Когда кто-то думает сделать преобразование Фурье для работы в обратной области, предполагается, что выполнение обратного преобразования вернет ту же функцию / вектор / что угодно. Другими словами, мы предполагаем

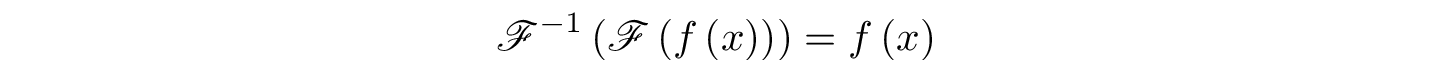
Это относится ко многим программам и библиотекам (например, Mathematica, Matlab / octave, Eigen/unsupported/FFT и т. Д.). Однако во многих библиотеках ( FFTW, KissFFT и т. Д.) Это не так, и существует тенденция к увеличению

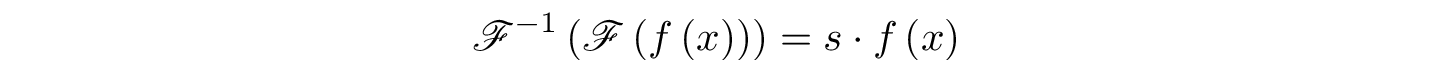
где s обычно это количество элементов (m) в массиве в степень чего-либо (должно быть 1, если не масштабировано несоответствующим образом как в преобразовании, так и в обратном порядке). Это сделано для того, чтобы воздерживаться от перебора всех m элементы умножаются на шкалу, что зачастую не важно.

Это сказанное, смотря на масштаб в обратной области, различные библиотеки, которые действительно масштабируют преобразования, могут использовать различные масштабы для преобразования и обратного преобразования. Общие пары масштабирования для преобразования / инверсии включают {m^-1, m} а также {m^-0.5, m^0.5}. Поэтому, сравнивая результаты из разных библиотек, мы должны быть готовы к факторам m (масштабируется m^-1 против не масштабируется), m^0.5 (масштабируется m^-0.5 против не масштабируется и масштабируется m^-1 против масштабируется m^-0.5) или даже другие шкалы, если были использованы другие коэффициенты масштабирования.

Примечание. Этот коэффициент масштабирования не связан с нормализацией массива, так что все значения [0,1] или что норма массива равна 1.