R - более быстрый способ расчета скользящей статистики по переменному интервалу
Мне любопытно, может ли кто-нибудь придумать (более быстрый) способ расчета скользящей статистики (скользящее среднее, медиана, процентили и т. Д.) За переменный интервал времени (оконное управление).
То есть, предположим, что каждому дается случайное время наблюдений (т. Е. Не ежедневные или еженедельные данные, наблюдения просто имеют метку времени, как в данных тиков), и предположим, что вы хотите посмотреть статистику центра и дисперсии, которую вы можете расширить и сузить интервал времени, в течение которого рассчитывается эта статистика.
Я сделал простой цикл, который делает это. Но он, очевидно, работает очень медленно (на самом деле я думаю, что мой цикл все еще работает на небольшом образце данных, которые я настроил для проверки его скорости). Я пытался заставить что-то наподобие ddply сделать это - что кажется нелегким делом, чтобы бегать за ежедневной статистикой - но, похоже, я не могу выбраться из этого.
Пример:
Образец настройки:
df <- data.frame(Date = runif(1000,0,30))
df$Price <- I((df$Date)^0.5 * (rnorm(1000,30,4)))
df$Date <- as.Date(df$Date, origin = "1970-01-01")
Пример функции (которая работает очень медленно со многими наблюдениями
SummaryStats <- function(dataframe, interval){
# Returns daily simple summary stats,
# at varying intervals
# dataframe is the data frame in question, with Date and Price obs
# interval is the width of time to be treated as a day
firstDay <- min(dataframe$Date)
lastDay <- max(dataframe$Date)
result <- data.frame(Date = NULL,
Average = NULL, Median = NULL,
Count = NULL,
Percentile25 = NULL, Percentile75 = NULL)
for (Day in firstDay:lastDay){
dataframe.sub = subset(dataframe,
Date > (Day - (interval/2))
& Date < (Day + (interval/2)))
nu = data.frame(Date = Day,
Average = mean(dataframe.sub$Price),
Median = median(dataframe.sub$Price),
Count = length(dataframe.sub$Price),
P25 = quantile(dataframe.sub$Price, 0.25),
P75 = quantile(dataframe.sub$Price, 0.75))
result = rbind(result,nu)
}
return(result)
}
Ваш совет будет приветствоваться!
4 ответа
Rcpp - это хороший подход, если скорость - ваша главная задача. Я буду использовать скользящую среднюю статистику, чтобы объяснить на примере.
Тесты: Rcpp против R
x = sort(runif(25000,0,4*pi))
y = sin(x) + rnorm(length(x),0.5,0.5)
system.time( rollmean_r(x,y,xout=x,width=1.1) ) # ~60 seconds
system.time( rollmean_cpp(x,y,xout=x,width=1.1) ) # ~0.0007 seconds
Код для функции Rcpp и R
cppFunction('
NumericVector rollmean_cpp( NumericVector x, NumericVector y,
NumericVector xout, double width) {
double total=0;
unsigned int n=x.size(), nout=xout.size(), i, ledge=0, redge=0;
NumericVector out(nout);
for( i=0; i<nout; i++ ) {
while( x[ redge ] - xout[i] <= width && redge<n )
total += y[redge++];
while( xout[i] - x[ ledge ] > width && ledge<n )
total -= y[ledge++];
if( ledge==redge ) { out[i]=NAN; total=0; continue; }
out[i] = total / (redge-ledge);
}
return out;
}')
rollmean_r = function(x,y,xout,width) {
out = numeric(length(xout))
for( i in seq_along(xout) ) {
window = x >= (xout[i]-width) & x <= (xout[i]+width)
out[i] = .Internal(mean( y[window] ))
}
return(out)
}
Теперь для объяснения rollmean_cpp, x а также y это данные. xout является вектором точек, в которых запрашивается скользящая статистика. width ширина *2 скользящего окна. Обратите внимание, что индексы для концов скользящего окна хранятся в ledge а также redge, По сути, это указатели на соответствующие элементы в x а также y, Эти индексы могут быть очень полезны для вызова других функций C++ (например, медиана и т. П.), Которые принимают вектор и начальные и конечные индексы в качестве входных данных.
Для тех, кто хочет "многословную" версию rollmean_cpp для отладки (длительно):
cppFunction('
NumericVector rollmean_cpp( NumericVector x, NumericVector y,
NumericVector xout, double width) {
double total=0, oldtotal=0;
unsigned int n=x.size(), nout=xout.size(), i, ledge=0, redge=0;
NumericVector out(nout);
for( i=0; i<nout; i++ ) {
Rcout << "Finding window "<< i << " for x=" << xout[i] << "..." << std::endl;
total = 0;
// numbers to push into window
while( x[ redge ] - xout[i] <= width && redge<n ) {
Rcout << "Adding (x,y) = (" << x[redge] << "," << y[redge] << ")" ;
Rcout << "; edges=[" << ledge << "," << redge << "]" << std::endl;
total += y[redge++];
}
// numbers to pop off window
while( xout[i] - x[ ledge ] > width && ledge<n ) {
Rcout << "Removing (x,y) = (" << x[ledge] << "," << y[ledge] << ")";
Rcout << "; edges=[" << ledge+1 << "," << redge-1 << "]" << std::endl;
total -= y[ledge++];
}
if(ledge==n) Rcout << " OVER ";
if( ledge==redge ) {
Rcout<<" NO DATA IN INTERVAL " << std::endl << std::endl;
oldtotal=total=0; out[i]=NAN; continue;}
Rcout << "For interval [" << xout[i]-width << "," <<
xout[i]+width << "], all points in interval [" << x[ledge] <<
", " << x[redge-1] << "]" << std::endl ;
Rcout << std::endl;
out[i] = ( oldtotal + total ) / (redge-ledge);
oldtotal=total+oldtotal;
}
return out;
}')
x = c(1,2,3,6,90,91)
y = c(9,8,7,5.2,2,1)
xout = c(1,2,2,3,6,6.1,13,90,100)
a = rollmean_cpp(x,y,xout=xout,2)
# Finding window 0 for x=1...
# Adding (x,y) = (1,9); edges=[0,0]
# Adding (x,y) = (2,8); edges=[0,1]
# Adding (x,y) = (3,7); edges=[0,2]
# For interval [-1,3], all points in interval [1, 3]
#
# Finding window 1 for x=2...
# For interval [0,4], all points in interval [1, 3]
#
# Finding window 2 for x=2...
# For interval [0,4], all points in interval [1, 3]
#
# Finding window 3 for x=3...
# For interval [1,5], all points in interval [1, 3]
#
# Finding window 4 for x=6...
# Adding (x,y) = (6,5.2); edges=[0,3]
# Removing (x,y) = (1,9); edges=[1,3]
# Removing (x,y) = (2,8); edges=[2,3]
# Removing (x,y) = (3,7); edges=[3,3]
# For interval [4,8], all points in interval [6, 6]
#
# Finding window 5 for x=6.1...
# For interval [4.1,8.1], all points in interval [6, 6]
#
# Finding window 6 for x=13...
# Removing (x,y) = (6,5.2); edges=[4,3]
# NO DATA IN INTERVAL
#
# Finding window 7 for x=90...
# Adding (x,y) = (90,2); edges=[4,4]
# Adding (x,y) = (91,1); edges=[4,5]
# For interval [88,92], all points in interval [90, 91]
#
# Finding window 8 for x=100...
# Removing (x,y) = (90,2); edges=[5,5]
# Removing (x,y) = (91,1); edges=[6,5]
# OVER NO DATA IN INTERVAL
print(a)
# [1] 8.0 8.0 8.0 8.0 5.2 5.2 NaN 1.5 NaN
Давайте посмотрим... вы делаете цикл (очень медленный в R), делаете ненужные копии данных при создании подмножества и используете rbind чтобы накопить ваш набор данных. Если вы избежите этого, все значительно ускорится. Попробуй это...
Summary_Stats <- function(Day, dataframe, interval){
c1 <- dataframe$Date > Day - interval/2 &
dataframe$Date < Day + interval/2
c(
as.numeric(Day),
mean(dataframe$Price[c1]),
median(dataframe$Price[c1]),
sum(c1),
quantile(dataframe$Price[c1], 0.25),
quantile(dataframe$Price[c1], 0.75)
)
}
Summary_Stats(df$Date[2],dataframe=df, interval=20)
firstDay <- min(df$Date)
lastDay <- max(df$Date)
system.time({
x <- sapply(firstDay:lastDay, Summary_Stats, dataframe=df, interval=20)
x <- as.data.frame(t(x))
names(x) <- c("Date","Average","Median","Count","P25","P75")
x$Date <- as.Date(x$Date)
})
dim(x)
head(x)
В ответ на мой вопрос к "Кевину" выше, я думаю, что понял кое-что ниже.
Эта функция берет данные о тиках (наблюдения за временем приходят через случайные интервалы и обозначаются меткой времени) и вычисляет среднее значение за интервал.
library(Rcpp)
cppFunction('
NumericVector rollmean_c2( NumericVector x, NumericVector y, double width,
double Min, double Max) {
double total = 0, redge,center;
unsigned int n = (Max - Min) + 1,
i, j=0, k, ledge=0, redgeIndex;
NumericVector out(n);
for (i = 0; i < n; i++){
center = Min + i + 0.5;
redge = center - width / 2;
redgeIndex = 0;
total = 0;
while (x[redgeIndex] < redge){
redgeIndex++;
}
j = redgeIndex;
while (x[j] < redge + width){
total += y[j++];
}
out[i] = total / (j - redgeIndex);
}
return out;
}')
# Set up example data
x = seq(0,4*pi,length.out=2500)
y = sin(x) + rnorm(length(x),0.5,0.5)
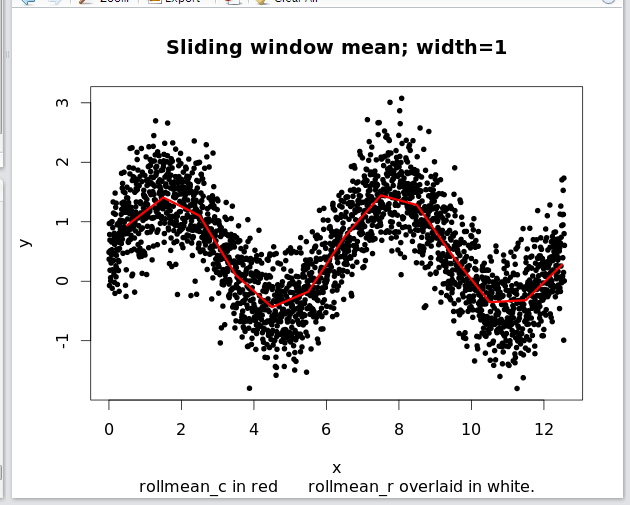
plot(x,y,pch=20,col="black",
main="Sliding window mean; width=1",
sub="rollmean_c in red rollmean_r overlaid in white.")
c.out = rollmean_c2(x,y,width=1,Min = min(x), Max = max(x))
lines(0.5:12.5,c.out,col="red",lwd=3)
Думайте обо всех пунктах, связанных как цепь. Думайте об этой цепочке как о графике, где каждая точка данных является узлом. Затем для каждого узла мы хотим найти все остальные узлы, которые находятся на расстоянии w или меньше. Чтобы сделать это, я сначала генерирую матрицу, которая дает попарные расстояния. nая строка дает расстояние для узлов n узлы друг от друга.
# First, some data
x = sort(runif(25000,0,4*pi))
y = sin(x) + rnorm(length(x),0,0.5)
# calculate the rows of the matrix one by one
# until the distance between the two closest nodes is greater than w
# This algorithm is actually faster than `dist` because it usually stops
# much sooner
dl = list()
dl[[1]] = diff(x)
i = 1
while( min(dl[[i]]) <= w ) {
pdl = dl[[i]]
dl[[i+1]] = pdl[-length(pdl)] + dl[[1]][-(1:i)]
i = i+1
}
# turn the list of the rows into matrices
rarray = do.call( rbind, lapply(dl,inf.pad,length(x)) )
larray = do.call( rbind, lapply(dl,inf.pad,length(x),"right") )
# extra function
inf.pad = function(x,size,side="left") {
if(side=="left") {
x = c( x, rep(Inf, size-length(x) ) )
} else {
x = c( rep(Inf, size-length(x) ), x )
}
x
}
Затем я использую матрицы для определения края каждого окна. Для этого примера я установил w=2,
# How many data points to look left or right at each data point
lookr = colSums( rarray <= w )
lookl = colSums( larray <= w )
# convert these "look" variables to indeces of the input vector
ri = 1:length(x) + lookr
li = 1:length(x) - lookl
С определенными окнами довольно просто использовать *apply функции, чтобы получить окончательный ответ.
rolling.mean = vapply( mapply(':',li,ri), function(i) .Internal(mean(y[i])), 1 )
Весь приведенный выше код занял около 50 секунд на моем компьютере. Это немного быстрее, чем rollmean_r функция в моем другом ответе. Тем не менее, особенно приятным здесь является то, что индейцы предоставляются. Затем вы можете использовать любую функцию R с *apply функции. Например,
rolling.mean = vapply( mapply(':',li,ri),
function(i) .Internal(mean(y[i])), 1 )
занимает около 5 секунд. А также,
rolling.median = vapply( mapply(':',li,ri),
function(i) median(y[i]), 1 )
занимает около 14 секунд. Если вы хотите, вы можете использовать функцию Rcpp в моем другом ответе, чтобы получить значения.