Алгоритм нахождения числовой перестановки по заданному лексикографическому индексу
Я ищу алгоритм, который дает набор чисел (например, 1 2 3) и индекс (например, 2), даст мне вторую перестановку этих чисел в соответствии с лексикографическим порядком. Например, в этом случае алгоритм вернет 1 3 2.
4 ответа
Вот простое решение:
from math import factorial # python math library
i = 5 # i is the lexicographic index (counting starts from 0)
n = 3 # n is the length of the permutation
p = range(1, n + 1) # p is a list from 1 to n
for k in range(1, n + 1): # k goes from 1 to n
f = factorial(n - k) # compute factorial once per iteration
d = i // f # use integer division (like division + floor)
print(p[d]), # print permuted number with trailing space
p.remove(p[d]) # delete p[d] from p
i = i % f # reduce i to its remainder
Выход:
3 2 1
Сложность времени O(n ^ 2), если p является списком, и O(n) амортизируется, если p это хеш-таблица и factorial предварительно вычислено.
Вот пример решения в Scala, которое я подробно объясню:
/**
example: index:=15, list:=(1, 2, 3, 4)
*/
def permutationIndex (index: Int, list: List [Int]) : List [Int] =
if (list.isEmpty) list else {
val len = list.size // len = 4
val max = fac (len) // max = 24
val divisor = max / len // divisor = 6
val i = index / divisor // i = 2
val el = list (i)
el :: permutationIndex (index - divisor * i, list.filter (_ != el)) }
Поскольку Scala не так хорошо известен, я думаю, что должен объяснить последнюю строчку алгоритма, которая, кроме этого, довольно понятна.
el :: elist
Создает новый список из элемента el и списка elist. Элист это рекурсивный вызов.
list.filter (_ != el)
это просто список без элемента эл.
Проверьте это исчерпывающе с небольшим списком:
(0 to fac (4) - 1).map (permutationIndex (_, List (1, 2, 3, 4))).mkString ("\n")
Проверьте скорость большего списка с 2 примерами:
scala> permutationIndex (123456789, (1 to 12).toList)
res45: List[Int] = List(4, 2, 1, 5, 12, 7, 10, 8, 11, 6, 9, 3)
scala> permutationIndex (123456790, (1 to 12).toList)
res46: List[Int] = List(4, 2, 1, 5, 12, 7, 10, 8, 11, 9, 3, 6)
Результат появляется сразу на 5-летнем ноутбуке. Существует 479 001 600 перестановок для Списка из 12 элементов, но с 100 или 1000 элементами это решение все равно должно работать быстро - вам просто нужно будет использовать BigInt в качестве индекса.
Как это работает? Я сделал график, для визуализации примера, список (1, 2, 3, 4) и индекс 15:
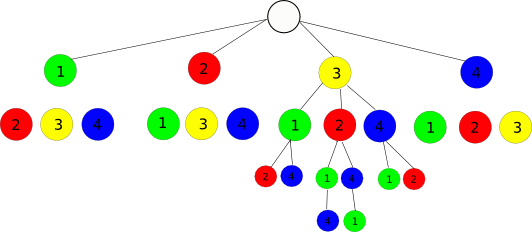
Список 4 Элементов производит 4! перестановки (=24). Мы выбираем произвольный индекс от 0 до 4!-1, скажем, 15.
Мы можем визуализировать все перестановки в дереве с первым узлом из 1..4. Мы делим 4! на 4 и видим, что каждый первый узел ведет к 6 поддеревьям. Если мы разделим наш индекс 15 на 6, результат будет 2, а значение в нашем нулевом списке с индексом 2 равно 3. Таким образом, первый узел равен 3, а остальная часть нашего списка равна (1, 2, 4), Вот таблица, показывающая, как 15 приводит к элементу с индексом 2 в массиве / списке / что угодно:
0 1 2 3 4 5 | 6 ... 11 | 12 13 14 15 16 17 | 18 ... 23
0 | 1 | 2 | 3
| | 0 1 2 3 4 5 |
Теперь мы вычтем 12, первый элемент ячейки (12...17) для последних 3 элементов, которые имеют 6 возможных перестановок, и посмотрим, как 15 отображается на 3. Число 3 теперь приводит к индексу массива 1, который был элемент 2, поэтому результат пока List (3, 2, ...).
| 0 1 | 2 3 | 4 5 |
| 0 | 1 | 3 |
| 0 1 |
Опять же, мы вычитаем 2 и заканчиваем двумя оставшимися элементами с 2 перестановками и индексом (0, 3), сопоставляя значения (1, 4). Мы видим, что второй элемент, принадлежащий 15 сверху, отображается на значение 3, а оставшийся элемент для последнего шага является другим:
| 0 | 1 |
| 0 | 3 |
| 3 | 0 |
Наш результат - Список (3, 2, 4, 1) или индексы (2, 1, 3, 0). Проверка всех индексов по порядку показывает, что они дают все перестановки по порядку.
Ссылка на упомянутую статью: http://penguin.ewu.edu/~trolfe/
/* Converting permutation index into a permutation
* From code accompanying "Algorithm Alley: Randomized Shuffling",
* Dr. Dobb’s Journal, Vol. 25, No. 1 (January 2000)
* http://penguin.ewu.edu/~trolfe/#Shuffle
*
* Author: Tim Rolfe
* RolfeT@earthlink.net
* http://penguin.ewu.edu/~trolfe/
*/
#include <stdio.h>
#include <stdlib.h>
// http://stackru.com/questions/8940470/algorithm-for-finding-numerical-permutation-given-lexicographic-index
// Invert the permutation index --- generate what would be
// the subscripts in the N-dimensional array with dimensions
// [N][N-1][N-2]...[2][1]
void IndexInvert(int J[], int N, int Idx)
{ int M, K;
for (M=1, K=N-1; K > 1; K--) // Generate (N-1)!
M *= K;
for ( K = 0; M > 1; K++ )
{ J[K] = Idx / M; // Offset in dimension K
Idx = Idx % M; // Remove K contribution
M /= --N; // next lower factorial
}
J[K] = Idx; // Right-most index
}
// Generate a permutation based on its index / subscript set.
// To generate the lexicographic order, this involves _shifting_
// characters around rather than swapping. Right-hand side must
// remain in lexicographic order
void Permute (char Line[], char first, int N, int Jdx[])
{ int Limit;
Line[0] = first;
for (Limit = 1; Limit < N; Limit++)
Line[Limit] = (char)(1+Line[Limit-1]);
for (Limit = 0; Limit < N; Limit++)
{ char Hold;
int Idx = Limit + Jdx[Limit];
Hold = Line[Idx];
while (Idx > Limit)
{ Line[Idx] = Line[Idx-1];
Idx--;
}
Line[Idx] = Hold;
}
}
// Note: hard-coded to generate permutation in the set [abc...
int main(int argc, char** argv)
{ int N = argc > 1 ? atoi(argv[1]) : 4;
char *Perm = (char*) calloc(N+1, sizeof *Perm);
int *Jdx = (int*) calloc(N, sizeof *Jdx);
int Index = argc > 2 ? atoi(argv[2]) : 23;
int K, Validate;
for (K = Validate = 1; K <= N; K++)
Validate *= K;
if (Index < 0 || Index >= Validate)
{ printf("Invalid index %d: %d! is %d\n", Index, N, Validate);
return -1; // Error return
}
IndexInvert(Jdx, N, Index);
Permute (Perm, 'a', N, Jdx);
printf("For N = %d, permutation %d in [0..%d] is %s\n",
N, Index, Validate-1, Perm);
return 0; // Success return
}
Так как вы не указали, на каком языке вы хотите, вот реализация на python.
Вам нужно только получить n-й элемент последовательности.
Одна идея алгоритма может состоять в том, чтобы сгенерировать последовательность, представляющую декартово произведение входной последовательности, и повторить ее, пропуская элементы с повторяющимися элементами.
Обратите внимание, что это может быть не самый быстрый способ сделать это, но, безусловно, это простой. Для быстрого см. Ответ киборга.