Способ группировки копланарных треугольников в сетке ТРИЙС?

Question

Я работаю над инструментом моделирования, который позволяет вам напрямую манипулировать сетками. Например, вы можете взять лицо и перетащить его. Восприятие пользователем "лица" может иметь более одного копланарного треугольника. Например, верхняя "грань" куба на самом деле будет двумя треугольниками, которые объединяются в один квадрат.

Для этого я хотел бы собрать все копланарные смежные грани к любому конкретному треугольнику для использования при перетаскивании. Я рассмотрел Simplifier, а также этот пост в качестве примеров, но я хочу сохранить лежащие в основе треугольники, а не уменьшать / удалять их.

В старые добрые времена вы строили модель ребер аля Мантля, где вы могли пройтись по каждому ребру, чтобы увидеть соседние грани и проверить нормали.

Я надеялся, что где-то для THREEJS уже будет написан какой-то код, который группирует компланарные треугольники вместе. Если я напишу это с нуля, лучший алгоритм, который я смогу придумать, это O(n^2), что-то вроде:

1. Создайте хэш ребер (в обоих направлениях), пройдя все вершины всех граней. Каждая запись представляет собой массив из 2 указателей лица. Вам нужно сделать этот шаг только один раз, когда сетка создается или изменяется.
2. Когда пользователь выбирает лицо для манипуляции, создайте пустой стек оценки и поместите выбранное лицо в этот стек. Также создайте пустой копланарный массив граней.
3. Выкиньте лицо из стека оценки и обойдите края этого лица. Посмотрите на все грани, смежные с этим краем в хэше. Если грань копланарна, поместите эту грань в стек оценки и сохраните в массиве копланарной грани.
4. Повторите шаги 3-4, пока стек оценки не станет пустым.

Когда этот алгоритм завершится, у вас должен быть массив всех граней, копланарных и смежных с гранью, с которой вы начинаете. Но это кажется относительно неэффективным для меня.

Любые предложения и указатели приветствуются!

Answer 1

Ваша идея работает.

Я добавил угловой порог, чтобы вы могли получить слегка некомпланарную топографию. Мне пришлось сделать onEvent, чтобы учесть неопределенное время рекурсии. Его следует изменить, чтобы вместо него поместить vertexHash в mesh.userData.

//редактировать. Я обновил класс, чтобы использовать параметр зажима, который позволяет вам зажимать maxAngle к исходной грани, когда установлено значение true. Если установлено значение false, оно будет сравнивать каждое лицо со следующим лицом.

faceUtils = function(){};
faceUtils.vertexHash = function(geometry){
  geometry.vertexHash = [];
  var faces = geometry.faces;
  var vLen = geometry.vertices.length;
  for(var i=0;i<vLen;i++){
    geometry.vertexHash[i] = [];
    for(var f in faces){
         if(faces[f].a == i || faces[f].b == i || faces[f].c == i){
            geometry.vertexHash[i].push(faces[f]);
       }
     }
   }
}

faceUtils.prototype.getCoplanar = function(maxAngle, geometry, face, clamp, out, originFace){
  if(clamp == undefined){
      clamp = true;
  }
  if(this.originFace == undefined){
    this.originFace = face;
  }
  if(this.pendingRecursive == undefined){
    this.pendingRecursive = 0;
  }
    this.result = out;
  if(out == undefined){
       this.result = {count:0};
  }
  if(geometry.vertexHash == undefined){
    faceUtils.vertexHash(geometry);
  }
  this.pendingRecursive++;
  var vertexes = ["a","b","c"];
  for (var i in vertexes){
    var vertexIndex = face[vertexes[i]];
    var adjacentFaces = geometry.vertexHash[vertexIndex];
    for(var a in adjacentFaces){
        var newface = adjacentFaces[a];
        var testF = this.originFace;
        if(clamp == false){
          testF = face
        }
        if(testF.normal.angleTo(newface.normal) * (180/ Math.PI) <= maxAngle){
          if(this.result["f"+newface.a+newface.b+newface.c] == undefined){
            this.result["f"+newface.a+newface.b+newface.c] = newface;
            this.result.count++;
            this.getCoplanar(maxAngle, geometry, newface, clamp, this.result, this.originFace);
          }
        }
    }
  }
  this.pendingRecursive--;

  if(this.pendingRecursive == 0 && this.onCoplanar != undefined){
    delete this.result.count;
    this.onCoplanar(this.result);
  }
}

Использование простое:

         var faceTools = new faceUtils();
         faceTools.onCoplanar = function(rfaces){
           for(var i in rfaces){
              rfaces[i].color.setHex(0xff0000);
              intersects[0].object.geometry.colorsNeedUpdate = true;
           }
         }
         //params: maxangle, geometry, picked face
         faceTools.getCoplanar(13, geometry, face);

Я добавил класс к чужой скрипке, и он отлично работает. http://jsfiddle.net/fnuaw44r/

Я обновил скрипку, чтобы использовать опцию зажима: http://jsfiddle.net/ta0g3mLc/

Я предполагаю, что это ужасно неэффективно, как вы предлагаете, но это зависит от сетки. Я добавил переменную pendingRecursive. Пока он не равен нулю, вы можете поднять gif и удалить его, когда значение снова равно нулю.

В любом случае, это отправная точка. Я уверен, что кто-то умный мог бросить через лица без вложенного цикла for.

Answer 2

Я закодировал решение, которое работает для меня, в соответствии с пунктами, указанными в вопросе, который я опубликовал изначально, и которое не использует рекурсию. Возможно, это будет кому-то полезно. (Примечание: я использую подчеркивание для удобства с хэшами, массивами и т. Д.).

Этот алгоритм сначала добавляет отображения на вершинах сетки, которые перечисляют все грани, которым принадлежит каждая вершина. Оттуда я могу начать с определенной грани, а затем искать все копланарные грани, которые имеют хотя бы одну вершину с начальной гранью (и идти оттуда). Если две вершины являются общими, это нормально.

var COPLANAR_ANGLE_TOLERANCE = .1; // degrees, not radians
var RAD_TO_DEG = 180 / Math.PI;
var FACELEN = 3; // meshes have triangles by default

function checkCoplanarity(f1, f2) {
  return ((f1.normal.angleTo(f2.normal) * RAD_TO_DEG) <= COPLANAR_ANGLE_TOLERANCE);
}

function assignVertexFaceHashes(geometry) {
  var vertices = geometry.vertices;
  var faces = geometry.faces, face;
  var theVertex;
  for (var faceIndex in faces) {
    face = geometry.faces[faceIndex];
    for (var vertIndex of [face.a, face.b, face.c]) {
      theVertex = vertices[vertIndex];
      if (!theVertex.hasOwnProperty('inFaces')) {
        theVertex.inFaces = {};
      }
      theVertex.inFaces[faceIndex] = true;
    }
  }
}


function findCoplanarAdjacentFaces(startFaceIndex, geometry) {
  var adjoiningFaceIndexes;
  var coplanarAdjacentFaces = {};
  var coplanarAdjacentVertices = {};
  var examQueue = [];
  var examined = {};
  var examFace, examFaceIndex;
  var adjoiningFace, adjoiningFaceIndex;
  var faces = geometry.faces;
  var vertices = geometry.vertices;
  var startFace = faces[startFaceIndex];
  examQueue.push(startFaceIndex);
  // include the start face as a coplanar face
  coplanarAdjacentVertices[startFace.a] = true;
  coplanarAdjacentVertices[startFace.b] = true;
  coplanarAdjacentVertices[startFace.c] = true;
  coplanarAdjacentFaces[startFaceIndex] = true; 
  // Map vertices back to all faces they belong to
  assignVertexFaceHashes(geometry);

  while (examQueue.length > 0) {
    examFaceIndex = examQueue.pop();
    examFace = faces[examFaceIndex];
    // console.log('examQueue:', examQueue.length);
    adjoiningFaceIndexes = [];
    for (var vertIndex of [examFace.a, examFace.b, examFace.c]) {
      adjoiningFaceIndexes = _.union(adjoiningFaceIndexes, _.map(_.keys(vertices[vertIndex].inFaces), function(c) { return parseInt(c); }));
    }
    //console.log('adjoiningFaceIndexes:', adjoiningFaceIndexes);
    for (adjoiningFaceIndex of adjoiningFaceIndexes) {
      //console.log('Examining adjoining face index:', adjoiningFaceIndex);
      if (!examined.hasOwnProperty(adjoiningFaceIndex)) {
        if ((adjoiningFaceIndex != examFaceIndex) && (!coplanarAdjacentFaces.hasOwnProperty(adjoiningFaceIndex))) {
          //console.log('adjoiningFaceIndex:', adjoiningFaceIndex);
          adjoiningFace = faces[adjoiningFaceIndex];
          if (checkCoplanarity(examFace, adjoiningFace)) {
            var overlap1 = [adjoiningFace.a, adjoiningFace.b, adjoiningFace.c];
            var overlap2 = [examFace.a, examFace.b, examFace.c];
            var vertsInCommon = _.intersection(overlap1, overlap2);
            // Check for vertices in common. If any vertices are in comment, these coplanar faces touch at least one vertex.
            if (vertsInCommon.length > 0) {
              //console.log('Pushing adjoining face due to vertices in common:', adjoiningFaceIndex);
              coplanarAdjacentFaces[adjoiningFaceIndex] = true;
              examQueue.push(adjoiningFaceIndex);
              coplanarAdjacentVertices[adjoiningFace.a] = true;
              coplanarAdjacentVertices[adjoiningFace.b] = true;
              coplanarAdjacentVertices[adjoiningFace.c] = true;
            } else {
              // it's possible the adjoining face only touches vertices to the middle of edges, so check for that.
              edgeIntersectExam:
              for (var i = 0; i < FACELEN; ++i) {
                adjoinP1 = overlap1[i];
                adjoinP2 = overlap1[(i + 1) % FACELEN];
                for (var j = 0; j < FACELEN; ++j) {
                  splitPoint = distToSegmentSquared3d(vertices[overlap2[j]], vertices[adjoinP1], vertices[adjoinP2]);
                  if (splitPoint.distance < POINT_ON_LINE_TOLERANCE) {
                    console.log('adding adjoining face due to edge intersection:', adjoiningFaceIndex);
                    console.log('j=', j, 'Source face:', examFaceIndex, examFace, 'We found split point on adjoining face index:', adjoiningFaceIndex, adjoiningFace);
                    coplanarAdjacentFaces[adjoiningFaceIndex] = true;
                    examQueue.push(adjoiningFaceIndex);
                    coplanarAdjacentVertices[adjoiningFace.a] = true;
                    coplanarAdjacentVertices[adjoiningFace.b] = true;
                    coplanarAdjacentVertices[adjoiningFace.c] = true;
                    break edgeIntersectExam;
                  }
                }
              }              
            }
          }
        }
      }
    }
    examined[examFaceIndex] = true;
  }

  return ({ faces: coplanarAdjacentFaces, vertices: coplanarAdjacentVertices });
}

function assignFacesToCoplanarGroups(csgPrimitive) {
  var geometry = csgPrimitive.geometry;
  var faceIndexList = _.mapObject(_.keys(geometry.faces), function() { return true; });
  var processedFaces = {};
  var coplanarFaces;
  var faces = geometry.faces;
  var intIndex;
  var coplanarGroupMax;
  var coplanarGroups = [];
  for (var processFaceIndex in faceIndexList) {
    intIndex = parseInt(processFaceIndex);
    if (!processedFaces.hasOwnProperty(intIndex)) {
      coplanars = findCoplanarAdjacentFaces(processFaceIndex, geometry);
      coplanarGroups.push({ faces: coplanars.faces, vertices: coplanars.vertices });
      coplanarGroupMax = coplanarGroups.length - 1;
      for (var groupedFaceIndex in coplanars.faces) {
        faces[groupedFaceIndex].coplanarGroupIndex = coplanarGroupMax;
        faces[groupedFaceIndex].color.setHex(0x0000ff); // just to help see the results
        processedFaces[groupedFaceIndex] = true;
      }
    }
  }
  geometry.coplanarGroups = coplanarGroups;
  geometry.colorsNeedUpdate = true;
}

function assignFacesToAllCoplanarGroups() {
  var now = new Date();
  var startTime = now.getTime();
  for (var csgPrimitive of csgPrimitives.children) {
    assignFacesToCoplanarGroups(csgPrimitive);
  }
  var later = new Date();
  var duration = later.getTime() - startTime;
  console.log('Done assigning faces to coplanar groups in:', duration, 'ms');
}

Вот как я это использую. У меня есть массив сеток (называемых csgPrimitives, потому что они взяты из ThreeCSG.js. Я вычисляю копланарные группы граней для каждого примитива и помещаю их в геометрию каждого примитива.

function assignFacesToAllCoplanarGroups() {
  var now = new Date();
  var startTime = now.getTime();
  for (var csgPrimitive of csgPrimitives.children) {
    assignFacesToCoplanarGroups(csgPrimitive);
  }
  var later = new Date();
  var duration = later.getTime() - startTime;
  console.log('Done assigning faces to coplanar groups in:', duration, 'ms');
}

Каждая результирующая копланарная группа содержит массив копланарных граней и массив уникальных вершин, используемых этими гранями. Используя массивы вершин, я могу теперь захватывать и перетаскивать все копланарные грани в меше, просто применяяфункцию Vector3.add().

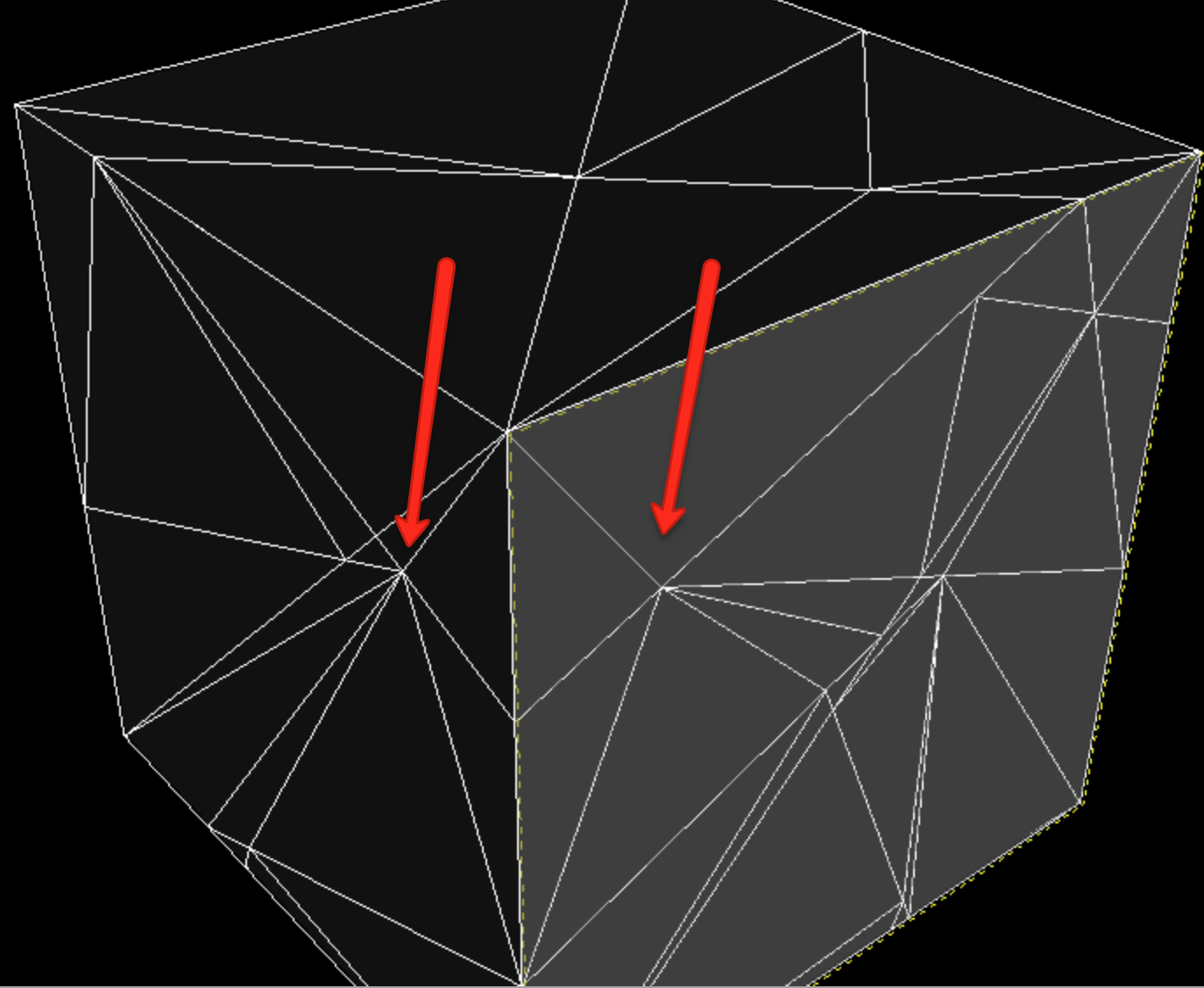
Причину этой работы можно уточнить на скриншоте ниже. Для создания показанной сетки был сгенерирован куб, а затем из него была вычтена логическая сфера с использованием библиотеки CSG, упомянутой выше.

  var box = new THREE.Mesh( new THREE.BoxGeometry( width, height, length ) );

  // CSG GEOMETRY
  cube_bsp = new ThreeBSP( box );

  var cutgeo = new THREE.SphereGeometry( 0.5,32,32 );

  // move geometry to where the cut should be
  var matrix = new THREE.Matrix4();
  matrix.setPosition( new THREE.Vector3(0.25, 0, 1.88) ); // NB: sphere does not intersect with cube
  cutgeo.applyMatrix( matrix );

  var sub =  new THREE.Mesh( cutgeo );
  var substract_bsp  = new ThreeBSP( sub );
  var subtract_bsp  = cube_bsp.subtract( substract_bsp );

  csgPrimitiveMesh = subtract_bsp.toMesh(); 

Сфера достаточно далеко, чтобы фактически не пересекаться с кубом, но, тем не менее, после операции у куба есть много дополнительных копланарных треугольников, но это не является согласованным граничным представлением. Например, как вы можете видеть на диаграмме, некоторые треугольники касаются середины ребер других треугольников (пара примеров обозначена красными стрелками).

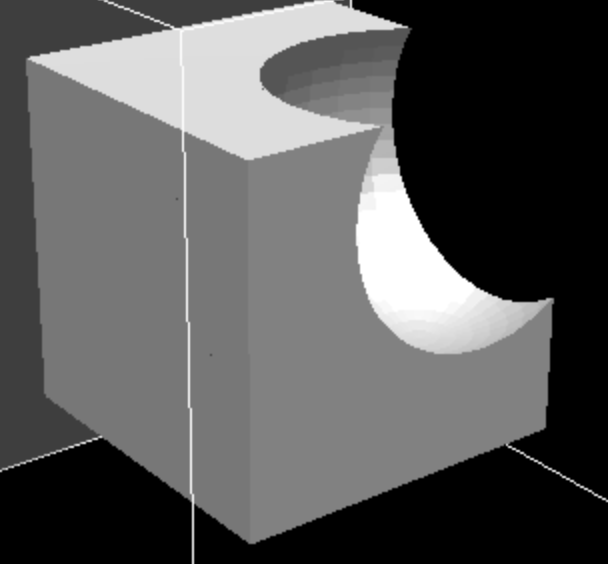
Я написал другой алгоритм, который пытается разделить треугольники дальше, когда треугольники соприкасаются вот так. Алгоритм несколько улучшает ситуацию:

но все же несовершенен, потому что библиотека CSG иногда создает треугольники, которые являются почти линиями (две вершины очень близко друг к другу), вызывая ошибки округления, которые отбрасывают мой алгоритм. Это также не очень хорошо работает, если край треугольника пересекается более чем одним другим треугольником в сетке.

Учитывая все это, в идеальном мире я бы на самом деле хотел бы объединить все копланарные грани в одно лицо, а затем сделать так, чтобы THREEjs правильно триангулировал результирующие (большие) грани (или использовал для этого какую-то другую библиотеку, например libtess).

Я ищу способ сделать это, теперь, когда у меня есть все компланарные треугольники, сгруппированные вместе. Мне кажется, что должен существовать алгоритм, который, учитывая все ребра всех этих компланарных треугольников, мог бы найти периметр всех из них. С этим я мог бы создать заново триангулированную грань, чтобы заменить их все, используя что-то вроде ShapeGeometry, чтобы создать новый набор треугольников для вставки в мою исходную сетку. Конечным результатом было бы, после применения всего этого, я бы вернулся к точной геометрии, которую THREEjs BoxGeometry создает в первую очередь после преобразования в BSP с помощью библиотеки CSG, а затем повторного преобразования в сетку.

Если у кого-то есть идеи о лучших способах достижения этой второй цели, пожалуйста, прокомментируйте. Если я найду какой-то хороший способ, я могу опубликовать его здесь. Прямо сейчас лучшие идеи, которые у меня есть:

Идея 1:

1. В наборе всех копланарных вершин среди смежных граней из вышеприведенного алгоритма найдите вершину, наиболее удаленную от начала координат.
2. Найдите все ребра, выходящие из этой вершины.
3. Пройдите по краю, который составляет минимальный угол от вектора от начала координат до этой вершины.
4. В следующей вершине пройдитесь по краю, который составляет максимальный угол к следующей вершине. (используйте dot() иcross(), чтобы убедиться, что вы правильно выбираете угол относительно нормали всех копланарных граней).
5. Остановитесь, когда достигнете первой вершины. Теоретически вы обошли весь периметр лица (теоретически!)

Идея 2 (лучевое литье):

1. Создайте коллекцию уникальных копланарных ребер из копланарных граней, найденных по вышеуказанному алгоритму
2. Отбросьте луч от каждой вершины в множестве копланарных вершин, найденном вышеупомянутым алгоритмом, вдоль любого копланарного ребра, которому он принадлежит.
3. Количество пересечений с другими вершинами и / или ребрами будет нечетным, если вершина является внутренней вершиной. Если это так, мы можем отбросить ребро, вдоль которого мы отбрасываем луч, а также эту внутреннюю вершину.
4. Теперь выберите любую оставшуюся вершину. Пройдите любой край, которому он принадлежит (теперь должно быть только два). Продолжайте ходить по совпадающим вершинам с ребрами (конечно, не следуя за предыдущим ребром), пока не вернетесь к начальной вершине. Теперь у нас должен быть периметр всех копланарных граней.

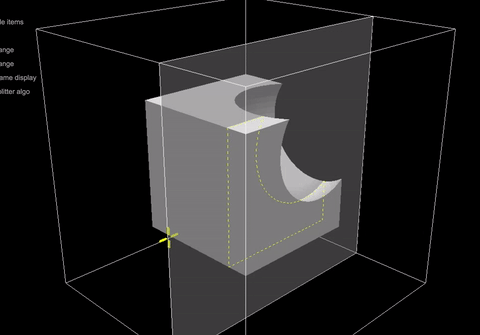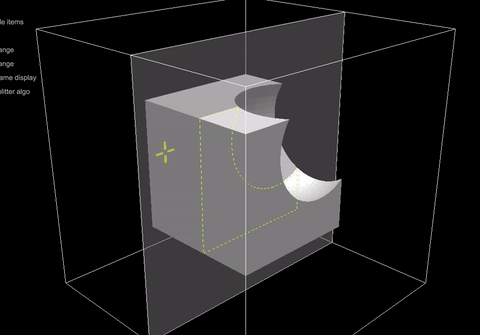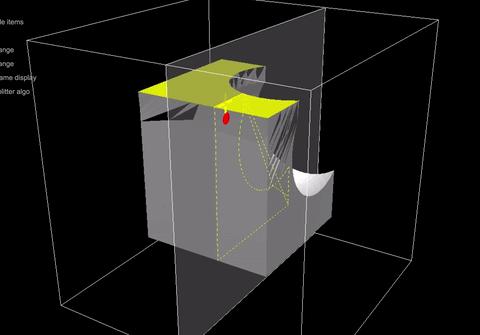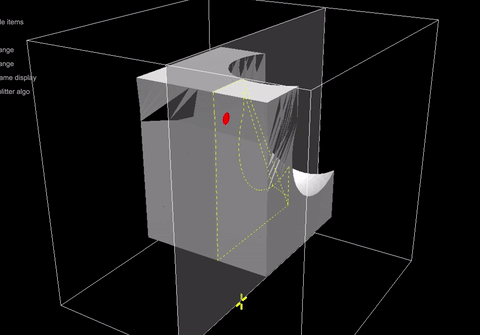
Чтобы увидеть, как библиотека CSG действительно создает слишком сложные грани, взгляните на сетку куба, когда вычитающая сфера действительно пересекает куб:

Как вы можете видеть, стороны куба, которые не должны быть затронуты логической операцией, имеют тонну внутренних треугольников.

Наконец, конечный результат перетаскивания этих грязных копланарных, но неправильных поверхностей сетки пограничного повторения показан на анимированном GIF ниже. Вы можете понять, почему я хочу упростить сетку, так как перетаскивание полностью портит сетку.