Как обновить MST после удаления ребра с графика?
У меня есть граф, представленный списками смежности, а его MST представлен родительским массивом.
Моя проблема в том, что мне нужно удалить ребро из графика и обновить родительский массив.
Мне уже удается делать случаи, когда:
- край не существует;
- ребро на графике, но не в MST (MST не изменяется);
- и ребро - единственный путь из двух узлов (в этом случае я возвращаю ноль, потому что граф не связан).
Что я могу сделать, если ребро в MST, а ребро в графе в цикле? Мне нужно сделать это в O(N + M) сложности.
Я пишу стоимость краев красным цветом.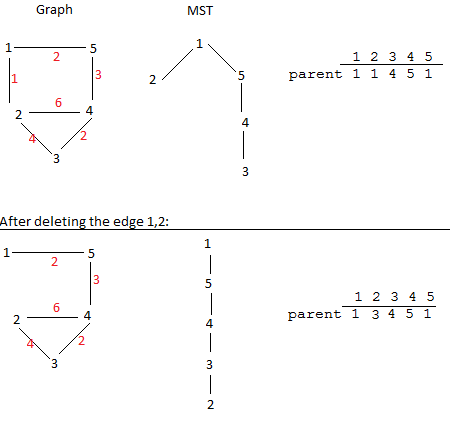
1 ответ
Просто найдите путь минимального расстояния отсоединенной теперь части дерева до остальной части дерева и добавьте этот путь между ними, который является одним ребром.
Скажем, ваше оригинальное дерево - T. С удалением края оно теперь разбито на деревья T1 и T2.
Возьми один из них - скажи Т2. Каждое ребро, инцидентное узлу на T2, находится либо на T2, либо является соединением T2 с T1. Среди этих ребер, инцидентных узлу на T2, выберите тот, который ( (имеет другой конец в узле T1) и (имеет минимальную стоимость среди всех таких ребер)). Поиск этого ребра, скажем, e=(u,v), занимает O(|E|) время. O(|N|), если отделенная часть является листом.
если бы существовало дерево, скажем, T', с меньшей стоимостью, чем T1 \union T2 \union {e}, тогда наборы узлов N1 и N2 в T1 и T2 имели бы больше взаимосвязей, чем только один ребро,
т. е. на T 'будет два или более ребер, которые начинаются в узле в N1 и заканчиваются в узле в N2. В противном случае ( (T1 и T2 являются минимальными связующими деревьями соответственно по N1 и N2) и (e является наименее дорогостоящим соединением между T1 и T2)), будет ложным. Но тогда любой переход между T1 и T2 обходится дороже, чем e=(u,v)- противоречит.
Пропущены некоторые подробности доказательства. надеюсь это поможет.