Как определить системы LTI с задержкой по времени в Scipy?

Question

Передаточная функция системы LTI с временной задержкой имеет числовой член exp(-Td * s), где Td - временная задержка. В Matlab такую ​​систему LTI можно создать разными способами (например, с помощью оператора "s" и установкой экспоненциального члена непосредственно или установкой inputdelayoutputdelay свойства tf объекты.) Однако, я не могу найти какой-либо способ сделать это в объектах Scipy Signal LTI. Я также проверил библиотеку систем управления Python, но так и не смог найти способ.

Я не хочу использовать приближение Паде для временной задержки и хочу установить точную задержку для системы LTI.

Кто-нибудь знает, как добиться этого в Scipy или в любой другой внешней библиотеке Python?

Answer 1

Я проверил модуль ltisys на github и попытался создать класс LTI с временной задержкой. Я думаю, было бы просто ввести задержку времени ввода в уравнение состояния, если мы заменим BU(t) на BU(t-Td), где Td - задержка времени. Следующий подход работает для системы с одним входом и одним выходом. Не может быть свободен от ошибок, но это решило мою цель.

#Inherit the parent LTI class  to create LTI class with time delay 


class ltidelay(lti):
    def __init__(self,inputdelay,*args,**kwargs):
        super(ltidelay,self).__init__(*args,**kwargs)    
        self.d =inputdelay

#define a method to simulate LTI with time delay . just copied lsim2 and made 2 changes. 1. passed the delay from the `ltidelay` object and 2. modified the state equation.


def lsim3(system , U=None, T=None,X0=None, **kwargs):
    if isinstance(system,lti):
        sys = system
    else:
        sys = lti(*system)
    delay = sys.d
    if X0 is  None:
        X0 = zeros(sys.B.shape[0],sys.A.dtype)        
    if T is None:
        T = linspace(0,10,101)
    T = atleast_1d(T)
    if len(T.shape) != 1:
        raise ValueError("T must be a rank1 array")
    if U is not None:
        U = atleast_1d(U)
        if len(U.shape)==1:
            U=U.reshape(-1,1)
        sU = U.shape
        if sU[0] != len(T):
            raise ValueError("U must have the same number of rows as elements in T")
        if sU[1] != sys.inputs:
            raise ValueError("The number of inputs in U is not compatible")
        ufunc = interpolate.interp1d(T, U, kind ='linear',axis =0,bounds_error =False)
        def fprime(x,t,sys,ufunc):
            return  dot(sys.A,x)+squeeze(dot(sys.B,nan_to_num(ufunc([t-delay]))))
        xout = odeint(fprime,X0,T,args=(sys,ufunc),**kwargs)
        yout = dot(sys.C,transpose(xout))
    else:
        def fprime(x,t,sys):
            return dot(sys.A,x)
        xout = odeint(fprime,X0,T,args=(sys,),**kwargs)
        yout = dot(sys.C, transpose(xout))
    return T , squeeze(transpose(yout)),xout   

#create an LTI system with delay 10

 tf = ltidelay(10,2,[4,1])

#create a step signal and time vector to simulate the LTI and check


u = linspace(0,0,100)

u[50:100] = 1

 t = linspace(1,100,100)

#check the simulation
y = lsim3(tf,u,t,X0 =0)

plot(y[1])

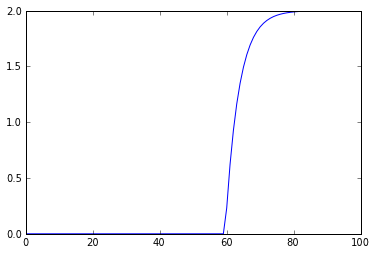
# compare with  LTI without time delay
y1 =lsim2(tf, u,t, X0=0)

plot(y1[1])

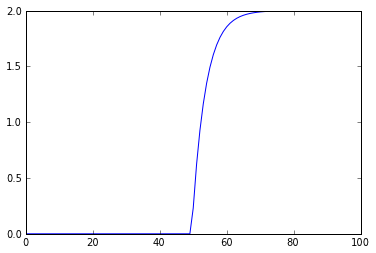
#delay works