Чем отличаются NP, NP-Complete и NP-Hard?
Чем отличаются NP, NP-Complete и NP-Hard?
Я знаю о многих ресурсах по всему Интернету. Я хотел бы прочитать ваши объяснения, и причина в том, что они могут отличаться от того, что там есть, или есть что-то, чего я не знаю.
12 ответов
Я предполагаю, что вы ищете интуитивные определения, так как технические определения требуют довольно много времени для понимания. Прежде всего, давайте вспомним предварительную необходимую концепцию, чтобы понять эти определения.
- Решение проблемы: проблема с ответом да или нет.
Теперь давайте определим эти классы сложности.
п
P - класс сложности, представляющий совокупность всех проблем решения, которые могут быть решены за полиномиальное время.
То есть, учитывая случай проблемы, ответ "да" или "нет" может быть решен за полиномиальное время.
пример
Учитывая связный граф G, можно ли раскрасить его вершины двумя цветами, чтобы ни одно ребро не было монохромным?
Алгоритм: начните с произвольной вершины, закрасьте ее красным, а все соседи - синим и продолжайте. Остановитесь, когда у вас закончились вершины или вы вынуждены сделать ребро, чтобы обе его конечные точки были одного цвета.
NP
NP- это класс сложности, представляющий набор всех проблем решения, для которых в случаях, когда ответ "да", есть доказательства, которые можно проверить за полиномиальное время.
Это означает, что если кто-то дает нам пример проблемы и сертификат (иногда называемый свидетелем), ответ на который да, мы можем проверить, что он правильный за полиномиальное время.
пример
Целочисленная факторизация в NP. Это проблема, которая дает целые числа n а также m есть целое число f с 1 < f < m такой, что f водоразделы n (f это небольшой фактор n)?
Это проблема решения, потому что ответы да или нет. Если кто-то передает нам пример проблемы (так что они передают нам целые числа n а также m) и целое число f с 1 < f < m и утверждают, что f является фактором n (сертификат), мы можем проверить ответ за полиномиальное время, выполнив деление n / f,
NP-Complete
NP-Complete - это класс сложности, представляющий множество всех задач. X в NP, для которого можно уменьшить любую другую проблему NP Y в X в полиномиальное время.
Интуитивно это означает, что мы можем решить Y быстро, если мы знаем, как решить X быстро. Точно, Y сводится к X, если есть алгоритм полиномиального времени f преобразовать экземпляры y из Y к случаям x = f(y) из X в полиномиальное время, с тем свойством, что ответ на y да, если и только если ответ на f(y) Да.
пример
3-SAT, Это проблема, в которой нам дано соединение (AND) из трехпозиционных дизъюнкций (OR), операторов вида
(x_v11 OR x_v21 OR x_v31) AND
(x_v12 OR x_v22 OR x_v32) AND
... AND
(x_v1n OR x_v2n OR x_v3n)
где каждый x_vij является булевой переменной или отрицанием переменной из конечного предопределенного списка (x_1, x_2, ... x_n),
Можно показать, что каждая проблема NP может быть уменьшена до 3-SAT. Доказательство этого является техническим и требует использования технического определения NP (на основе недетерминированных машин Тьюринга). Это известно как теорема Кука.
Что делает NP-полные задачи важными, так это то, что если для решения одной из них можно найти детерминированный алгоритм за полиномиальное время, то каждая проблема NP разрешима за полиномиальное время (одна задача - управлять ими всеми).
NP-трудной
Интуитивно понятно, что это проблемы, которые по крайней мере так же сложны, как и проблемы с NP-завершением. Обратите внимание, что NP-сложные проблемы не обязательно должны быть в NP, и они не должны быть проблемами решения.
Точное определение здесь заключается в том, что проблема X NP-сложный, если есть NP-полная проблема Y такой, что Y сводится к X в полиномиальное время.
Но поскольку любая NP-полная задача может быть сведена к любой другой NP-полной задаче за полиномиальное время, все NP-полные задачи могут быть сведены к любой NP-трудной задаче за полиномиальное время. Затем, если существует решение одной NP-трудной задачи за полиномиальное время, существует решение всех NP-задач за полиномиальное время.
пример
Проблема остановки - NP-трудная проблема. Это проблема, которую дала программа P и ввод I это остановит? Это проблема решения, но ее нет в NP. Ясно, что любая NP-полная проблема может быть сведена к этой. В качестве другого примера, любая NP-полная проблема является NP-сложной.
Моя любимая NP-полная проблема - проблема Сапер.
P = NP
Это одна из самых известных проблем в области компьютерных наук и один из самых важных нерешенных вопросов в математических науках. На самом деле, Институт Клэя предлагает миллион долларов для решения этой проблемы ( рецензия Стивена Кука на сайте Клэя довольно хорошая).
Понятно, что P является подмножеством NP. Открытый вопрос состоит в том, имеют ли проблемы NP детерминированные решения за полиномиальное время. Во многом считается, что они этого не делают. Вот выдающаяся недавняя статья о последней (и важности) проблеме P = NP: Состояние проблемы P против NP.
Лучшая книга на эту тему - " Компьютеры и неразрешимость " Гэри и Джонсона.
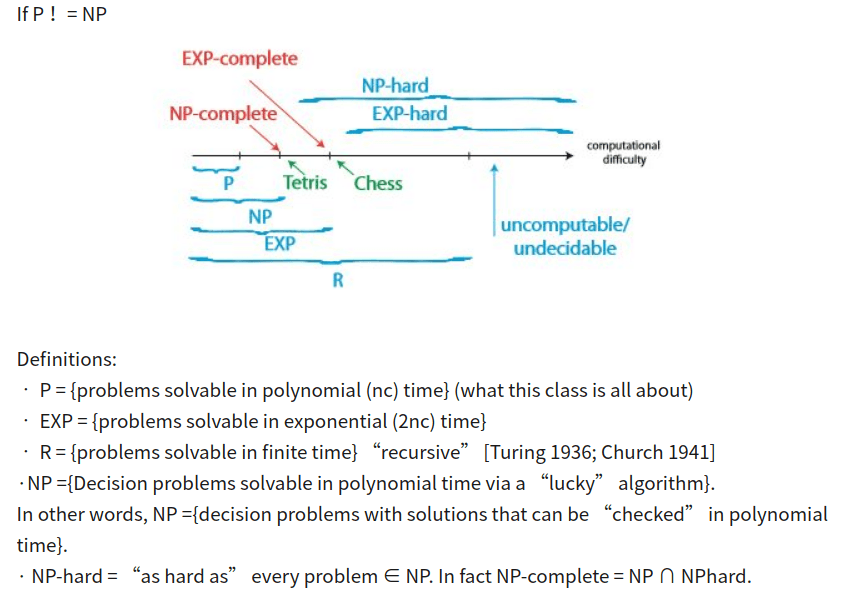
Я искал вокруг и видел много длинных объяснений. Вот небольшая диаграмма, которая может быть полезна для подведения итогов:
Обратите внимание, как сложность увеличивается сверху вниз: любой NP может быть уменьшен до NP-Complete, а любой NP-Complete может быть уменьшен до NP-Hard, все за P (полиномиальное) время.
Если вы можете решить более сложный класс задач за время P, это будет означать, что вы нашли способ решить все более простые задачи за время P (например, доказательство P = NP, если вы выясните, как решить любую задачу NP-Complete в Время р).
____________________________________________________________ | Тип проблемы | Проверяется в P время | Разрешимый в P время | Увеличение сложности ___________________________________________________________ | | | P | Да | Да | | | НП | Да | Да или нет * | | | NP-Complete | Да | Неизвестный | | | НП-Хард | Да или нет ** | Неизвестный *** | | ____________________________________________________________ V
Примечания о Yes или же No записей:
- * Проблема NP, также являющаяся P, разрешима за P время.
- ** Задача NP-Hard, которая также является NP-Complete, проверяется в течение P времени.
- *** Проблемы NP-Complete (все из которых составляют подмножество NP-hard) могут быть. В остальном НП труднее нет.
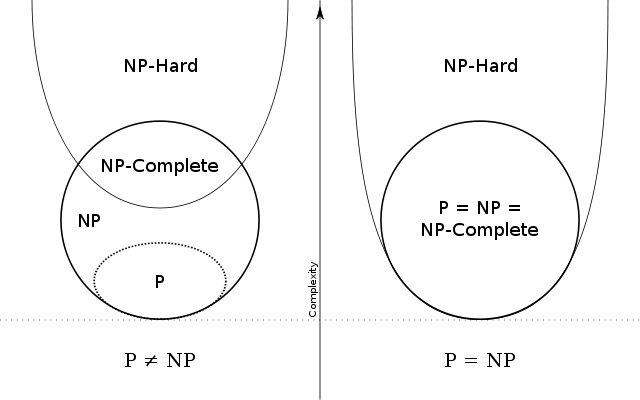
Я также нашел эту диаграмму весьма полезной, чтобы увидеть, как все эти типы соответствуют друг другу (уделите больше внимания левой половине диаграммы).
P (полиномиальное время): как следует из названия, это проблемы, которые можно решить за полиномиальное время.
NP (недетерминированное полиномиальное время): это задачи решения, которые можно проверить за полиномиальное время. Это означает, что если я утверждаю, что для конкретной проблемы есть решение за полиномиальное время, вы просите меня доказать это. Затем я дам вам доказательство, которое вы можете легко проверить за полиномиальное время. Такого рода проблемы называются проблемами NP. Обратите внимание, что здесь мы не говорим о том, есть ли решение этой проблемы за полиномиальное время или нет. Но мы говорим о проверке решения данной проблемы за полиномиальное время.
NP-Hard: Это по крайней мере так же сложно, как самые сложные проблемы в NP. Если мы сможем решить эти проблемы за полиномиальное время, мы сможем решить любую проблему NP, которая может существовать. Обратите внимание, что эти проблемы не обязательно являются проблемами NP. Это означает, что мы можем / не можем проверить решение этих проблем за полиномиальное время.
NP-Complete: это проблемы, которые являются как NP, так и NP-Hard. Это означает, что если мы можем решить эти проблемы, мы можем решить любую другую проблему NP, и решения этих проблем могут быть проверены за полиномиальное время.
Это очень неформальный ответ на заданный вопрос.
Можно ли записать 3233 как произведение двух других чисел, больших 1? Есть ли способ пройти путь по всем Семи Мостам Кенигсберга, не переходя ни один мост дважды? Это примеры вопросов, которые имеют общую черту. Может быть неочевидно, как эффективно определить ответ, но если ответ "да", то есть краткое и быстрое подтверждение. В первом случае нетривиальная факторизация 51; во втором - маршрут для прохождения мостов (с учетом ограничений).
Решение проблемы - это набор вопросов с ответами "да" или "нет", которые различаются только одним параметром. Скажите, что проблема СОСТАВЛЯЕТ ={ n композит ": n является целым числом} или EULERPATH={"Имеет ли граф G есть путь Эйлера?" G конечный граф}.
Теперь некоторые проблемы решения поддаются эффективным, если не очевидным алгоритмам. Эйлер открыл эффективный алгоритм для таких задач, как "Семь мостов Кенигсберга" более 250 лет назад.
С другой стороны, для многих проблем, связанных с принятием решения, неочевидно, как получить ответ, но если вы знаете какую-то дополнительную информацию, очевидно, как доказать, что вы правильно ответили. COMPOSITE выглядит следующим образом: пробное деление - это очевидный алгоритм, и он медленный: чтобы получить десятизначное число, нужно попробовать что-то вроде 100000 возможных делителей. Но если, например, кто-то сказал вам, что 61 - это делитель 3233, простое длинное деление - эффективный способ убедиться, что они верны.
Класс сложности NP - это класс проблем принятия решений, где ответы "да" должны быть краткими, чтобы быстро проверять доказательства. Как композит. Одним из важных моментов является то, что это определение ничего не говорит о том, насколько сложна проблема. Если у вас есть правильный и эффективный способ решения проблемы решения, достаточно просто записать шаги в решении.
Исследование алгоритмов продолжается, и все время создаются новые умные алгоритмы. Проблема, которую вы, возможно, не знаете, как эффективно решать сегодня, может оказаться эффективным (если не очевидным) решением завтра. На самом деле исследователям потребовалось до 2002 года, чтобы найти эффективное решение для КОМПОЗИТА! Со всеми этими достижениями действительно нужно задаться вопросом: действительно ли это немного о коротких доказательствах, просто иллюзия? Может быть, каждая проблема решения, которая поддается эффективным доказательствам, имеет эффективное решение? Никто не знает
Возможно, самый большой вклад в эту область внес открытие специфического класса проблем NP. Играя с моделями цепей для вычислений, Стивен Кук обнаружил проблему решения разновидности NP, которая была доказуемо такой же трудной или сложной, как любая другая проблема NP. Эффективное решение проблемы булевой выполнимости может быть использовано для создания эффективного решения любой другой проблемы в NP. Вскоре после этого Ричард Карп показал, что ряд других проблем решения может служить той же цели. Эти проблемы, в некотором смысле самые трудные проблемы в NP, стали называться NP-полными проблемами.
Конечно, NP - это всего лишь класс решения проблем. Многие проблемы естественно не формулируются таким образом: "найти факторы N", "найти кратчайший путь в графе G, который посещает каждую вершину", "дать набор переменных, присваивающих следующее булево выражение, истинное". Хотя можно неформально говорить о том, что некоторые такие проблемы находятся "в НП", технически это не имеет особого смысла - это не проблемы решения. Некоторые из этих проблем могут даже обладать такой же мощью, что и NP-полная проблема: эффективное решение этих (не связанных с решением) проблем приведет непосредственно к эффективному решению любой проблемы NP. Такая проблема называется NP-hard.
В дополнение к другим замечательным ответам, вот типичная схема, которую люди используют, чтобы показать разницу между NP, NP-Complete и NP-Hard:
Самый простой способ объяснить P v. NP и тому подобное, не вдаваясь в технические подробности, - это сравнить "проблемы со словами" с "проблемами с множественным выбором".
Когда вы пытаетесь решить "проблему слов", вы должны найти решение с нуля. Когда вы пытаетесь решить "проблему множественного выбора", у вас есть выбор: либо решите ее, как "проблему слова", либо попробуйте включить каждый из ответов, которые вам даны, и выберите подходящий вариант ответа.
Часто случается, что "проблема множественного выбора" намного проще, чем соответствующая "проблема слов": замена ответов кандидата и проверка их соответствия могут потребовать значительно меньших усилий, чем поиск правильного ответа с нуля.
Теперь, если бы мы согласились с тем, что полиномиальное время "легкое" требует усилий, тогда класс P будет состоять из "простых задач со словами", а класс NP будет состоять из "простых задач с множественным выбором".
Суть P v. NP заключается в вопросе: "Есть ли какие-нибудь простые проблемы с множественным выбором, которые не так просты, как проблемы со словами"? То есть, существуют ли проблемы, для которых легко проверить достоверность данного ответа, но трудно найти этот ответ с нуля?
Теперь, когда мы интуитивно понимаем, что такое NP, мы должны бросить вызов нашей интуиции. Оказывается, что есть "проблемы с множественным выбором", которые в некотором смысле являются наиболее сложными из всех них: если бы кто-то нашел решение одной из этих "самых трудных из всех" проблем, он мог бы найти решение для ВСЕХ. НП проблемы! Когда Кук обнаружил это 40 лет назад, это стало полной неожиданностью. Эти "самые сложные из всех" проблем известны как NP-hard. Если вы найдете "решение проблемы со словом" для одного из них, вы автоматически найдете "решение проблемы со словом" для каждой "простой задачи с множественным выбором"!
Наконец, NP-полными являются те проблемы, которые являются NP-сложными и NP-сложными. Следуя нашей аналогии, они являются одновременно "простыми, как проблемы с множественным выбором" и "самыми сложными из всех, как проблемы со словом".
NP-полными задачами являются те проблемы, которые являются NP-Hard и в классе сложности NP. Следовательно, чтобы показать, что любая заданная проблема является NP-полной, вам нужно показать, что проблема как в NP, так и в том, что она NP-сложная.
Задачи, находящиеся в классе сложности NP, могут быть решены недетерминированно за полиномиальное время, а возможное решение (т. Е. Сертификат) для задачи в NP может быть проверено на корректность за полиномиальное время.
Примером недетерминированного решения проблемы k-клика будет что-то вроде:
1) случайным образом выбрать k узлов из графика
2) проверить, что эти k узлов образуют клику.
Вышеприведенная стратегия является полиномиальной по размеру входного графа, и, следовательно, проблема k-клики находится в NP.
Заметим, что все задачи, детерминированно разрешимые за полиномиальное время, также есть в NP.
Демонстрация того, что проблема NP-сложная, как правило, включает в себя сокращение от некоторой другой NP-сложной проблемы к вашей проблеме с использованием полиномиального отображения времени: http://en.wikipedia.org/wiki/Reduction_(complexity)
Я думаю, что мы можем ответить на него гораздо более кратко. Я ответил на связанный вопрос и скопировал свой ответ оттуда
Но во-первых, NP-трудная задача - это проблема, для которой мы не можем доказать, что существует решение за полиномиальное время. NP-твердость некоторой "проблемы-P" обычно подтверждается путем преобразования уже доказанной NP-трудной проблемы в "проблему-P" за полиномиальное время.
Чтобы ответить на остальную часть вопроса, сначала нужно понять, какие сложные задачи также являются NP-полными. Если NP-сложная задача принадлежит NP, то она является NP-полной. Чтобы принадлежать к множеству NP, проблема должна быть
(i) решение проблемы,
(ii) число решений задачи должно быть конечным, и каждое решение должно иметь полиномиальную длину, и
(iii) учитывая решение по полиномиальной длине, мы должны быть в состоянии сказать, является ли ответ на проблему да / нетТеперь легко заметить, что может быть много сложных для NP задач, которые не относятся к множеству NP и которые труднее решить. В качестве интуитивно понятного примера, оптимизационная версия коммивояжера, в которой нам нужно найти фактическое расписание, сложнее, чем вариант решения коммивояжера, где нам просто нужно определить, существует ли расписание с длиной <= k или нет.
Есть действительно хорошие ответы на этот конкретный вопрос, поэтому нет смысла писать мое собственное объяснение. Поэтому я постараюсь поделиться с отличным ресурсом о различных классах вычислительной сложности.
Для тех, кто думает, что сложность вычислений касается только P и NP, вот самый исчерпывающий ресурс о различных проблемах вычислительной сложности. Помимо задач, поставленных OP, он перечислил около 500 различных классов вычислительных задач с хорошими описаниями, а также список фундаментальных исследовательских работ, которые описывают класс.
Насколько я понимаю, проблема np-hard не "сложнее", чем проблема np-complete. Фактически, по определению, каждая np-полная проблема:
- в НП
- нп твердолобый
-- Вступление. Алгоритмы (3ed) по Cormen, Leiserson, Rivest и Stein, стр. 1069
P (полиномиальное время)
Набор задач принятия решений, которые можно решить за полиномиальное время.
NP (недетерминированное полиномиальное время)
Набор проблем принятия решений, которые можно проверить за полиномиальное время .
Лемма: P ⊆ NP.
Проблема (в P ), которая может быть решена за полиномиальное время с помощью алгоритма, также может быть проверена за полиномиальное время с помощью того же алгоритма (следовательно, она находится в NP ).
Примечание : P ⊆ NP читается как: « P является подмножеством NP », и это означает, что либо P = NP , либо P ⊂ NP .
Проблема P и NP
Это нерешенная проблема с призом в 1000000 долларов США, которая является доказательством того, что:
P = NP Множество P равно множеству NP .
P ⊂ NP Множество P является собственным подмножеством множества NP .
(из чего следует, что P ≠ NP ).
NP-полный
Набор проблем принятия решений. Правильное подмножество NP (всегда можно проверить за полиномиальное время).
NP-полный ⊂ NP
Имеет следующие характеристики:
- Любую задачу в NP можно за полиномиальное время свести к задаче в NP-Complete.
- Если бы был найден алгоритм, способный решить любую NP-полную задачу, то такой алгоритм был бы способен решить любую задачу из NP . Такой алгоритм пока не найден.
Пример NP-полной задачи:
NP-жесткий
Набор проблем, не ограничивающийся проблемами принятия решений; по крайней мере, так же сложно, как проблемы в NP-complete.
NP-hard — это правильное расширение NP-complete. (может быть или не быть проверяемым за полиномиальное время).
NP-полный ⊂ NP-сложный
Имеет следующие характеристики:
- Любую задачу в NP-complete можно за полиномиальное время свести к задаче в NP-Hard.
- Если бы был найден алгоритм, способный решить любую NP-трудную задачу, то такой алгоритм был бы способен решить любую задачу из NP . Такой алгоритм пока не найден.
Пример NP-сложной задачи: SATSAT (так как NP-Complete ⊂ NP-Hard )
Пример NP-сложной , но не NP-полной задачи: Проблема остановки