Matlab - генерировать случайные неособые треугольные матрицы
Как я могу сгенерировать случайную треугольную матрицу? (верхний и нижний)
Обычно я использую rand(n) но если я попробую tril(rand(n)) это будет единственное число, и я не хочу этого.
2 ответа
Ваш ответ правильный:
A=tril(rand(n))
Вы можете проверить, что эта матрица не является единственной, используя
rcond(A)>eps
или же
min(svd(A))>eps
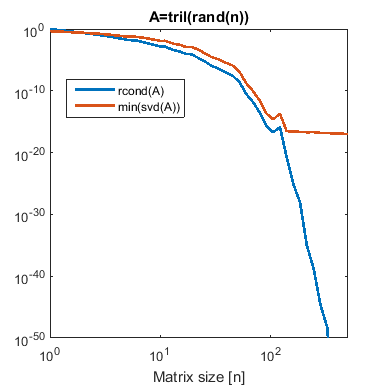
и проверка того, что наименьшее единственное значение больше, чем eps, или любой другой числовой допуск, который соответствует вашим потребностям. (код вернет 1 или 0). За n>50 Вы начнете подходить к единичным матрицам.
Вот небольшой анализ того, как матрица приближается к сингулярности с ее размером...
Хорошо, вот мысли о сингулярности треугольной матрицы. Детерминант треугольной матрицы - это то, что определяет сингулярность, потому что она входит в знаменатель при построении обратной матрицы. Свойство треугольной матрицы таково, что определитель равен произведению диагональных элементов.
Так что для матрицы NxN у нас на диагонали есть произведение iid U(0,1) чисел. Очевидно, что определитель будет уменьшаться как N увеличивается из-за того, что все числа <1 и больше у вас есть, тем меньше значение будет иметь продукт (иначе определитель).
Интересно проверить, что для det = X1X2... * XN среднее значение будет уменьшаться до 2-N, поскольку каждый член в произведении равен U(0,1) со средним значением 1/2, и все они iid. Альтернативной проверкой будет вычисление среднего значения из PDF-файла продукта (см. https://math.stackexchange.com/questions/659254/product-distribution-of-two-uniform-distribution-what-about-3-or-more), и, действительно, это даст вам точно такой же результат, 2-н. Также можно вычислить дисперсию детерминанта, поскольку второй импульс минус средний квадрат, и он равен (3-N-4-N).
Обратите внимание, что это средние значения, которые вы можете ожидать в среднем, скажем, если вы выберете 106 треугольных матриц с N=100, вычислите их определитель и усредните их, вы должны найти, что они довольно близки к 2-100.
Вот в чем проблема. В среднем треугольная случайная матрица экспоненциально переходит в сингулярность с ростом N, 2-10 примерно равно 1/1000. 2-20 примерно равно 1/1 000 000. Для N = 100 это должно быть в среднем около 10-30 или около того, что делает все упражнения спорными.
К сожалению, я не могу предложить ничего, кроме этого простого анализа.
Если вам нужна хорошо обусловленная случайная треугольная матрица, вы можете взять треугольную часть A2 с A = rand (n). Таким образом, triu (A * A) для любого размера n хорошо обусловлено, но, конечно, имеет сложность O (n3) для умножения матрицы на матрицу.