Задать операции (объединение, пересечение) на массиве Swift?
Существуют ли какие-либо стандартные библиотечные вызовы, которые я могу использовать для выполнения операций над множествами двух массивов или для реализации такой логики самостоятельно (в идеале как функционально, так и максимально эффективно)?
5 ответов
Да, у Свифта есть Set учебный класс.
let array1 = ["a", "b", "c"]
let array2 = ["a", "b", "d"]
let set1:Set<String> = Set(array1)
let set2:Set<String> = Set(array2)
Swift 3.0+ может выполнять операции над наборами как:
firstSet.union(secondSet)// Union of two sets
firstSet.intersection(secondSet)// Intersection of two sets
firstSet.symmetricDifference(secondSet)// exclusiveOr
Swift 2.0 может рассчитывать на аргументы массива:
set1.union(array2) // {"a", "b", "c", "d"}
set1.intersect(array2) // {"a", "b"}
set1.subtract(array2) // {"c"}
set1.exclusiveOr(array2) // {"c", "d"}
Swift 1.2+ может рассчитывать на комплекты:
set1.union(set2) // {"a", "b", "c", "d"}
set1.intersect(set2) // {"a", "b"}
set1.subtract(set2) // {"c"}
set1.exclusiveOr(set2) // {"c", "d"}
Если вы используете пользовательские структуры, вам нужно реализовать Hashable.
Спасибо Майклу Стерну в комментариях к обновлению Swift 2.0.
Спасибо Амджаду Хуссейни в комментариях за информацию о Hashable.
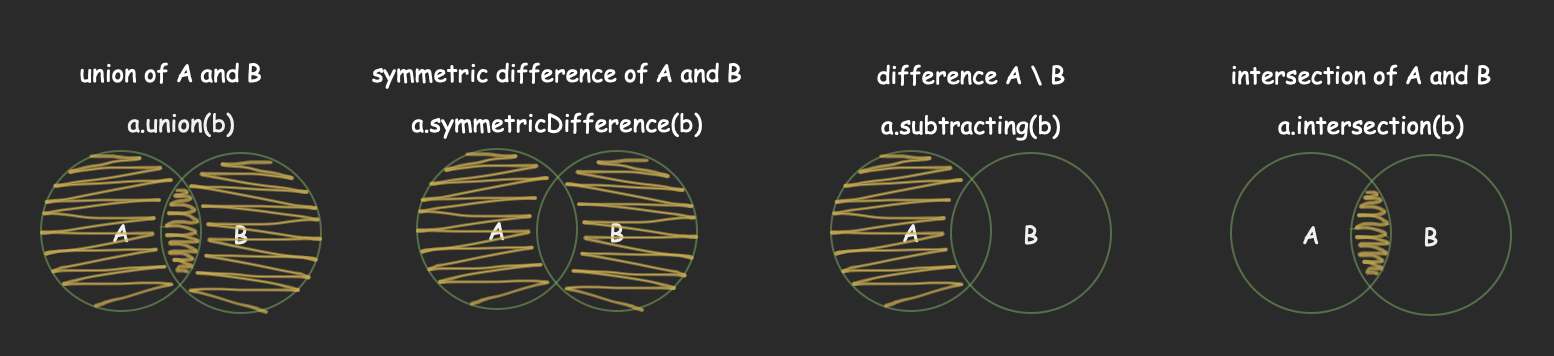
Операции Swift Set
Пример
let a: Set = ["A", "B"]
let b: Set = ["B", "C"]
союз А и Бa.union(b)
let result = a.union(b)
var a2 = a
a2.formUnion(b)
//["A", "B", "C"]
симметричная разность A и Ba.symmetricDifference(b)
let result = a.symmetricDifference(b)
//["A", "C"]
разница А\Вa.subtracting(b)
let result = a.subtracting(b)
//["A"]
пересечение улиц А и Бa.intersection(b)
let result = a.intersection(b)
//["B"]
Обратите внимание, что порядок результатов зависит от хэша
Самый эффективный метод, который я знаю, - это использование чисел Годеля. Google для кодирования godel.
Идея такова. Предположим, у вас есть N возможных чисел, и вам нужно составить их наборы. Например, N=100000 и хотите сделать наборы, такие как {1,2,3}, {5, 88, 19000} и т. Д.
Идея состоит в том, чтобы сохранить список из N простых чисел в памяти, и для заданного набора {a, b, c, ...} вы кодируете его как
prime[a]*prime[b]*prime[c]*...
Таким образом, вы кодируете набор как BigNumber. Операции с BigNumbers, несмотря на то, что они медленнее, чем операции с целыми числами, все еще очень быстрые.
Чтобы объединить 2 набора A, B, вы берете
UNITE(A, B) = lcm(a, b)
наименьшее общее кратное A и B, поскольку A и B являются множествами и обоими числами.
Чтобы сделать пересечение вы берете
INTERSECT(A, B) = gcd (a, b)
наибольший общий делитель.
и так далее.
Эта кодировка называется godelization, вы можете погуглить, все языки арифметики, написанные с использованием логики Фреге, могут кодироваться с использованием чисел таким образом.
Чтобы получить операцию является участником? это очень просто -
ISMEMBER(x, S) = remainder(s,x)==0
Чтобы получить кардинал, это немного сложнее -
CARDINAL(S) = # of prime factors in s
Вы разлагаете число S, представляющее множество на произведение простых факторов, и добавляете их показатели. В случае, если набор не допускает дублирования, у вас будут все показатели 1.
Стандартных библиотечных вызовов нет, но вы можете посмотреть библиотеку ExSwift. Он включает в себя множество новых функций в массивах, включая разность, пересечение и объединение.
Возможно, вы захотите следовать той же схеме, что и в Objective-C, в которой также отсутствуют такие операции, но есть простой обходной путь: