Кратчайший путь между необработанными географическими координатами и узлом графика
Я реализовал простой алгоритм Дейкстры для нахождения кратчайшего пути на карте.osm с Java.
Поиск пути в графе, который создается из файла.osm, работает довольно хорошо. Но если текущее местоположение и / или пункт назначения пользователя не является узлом этого графа (просто необработанные координаты), как мы можем "связать" эти координаты с графом, чтобы заставить поиск пути работать?
Простое простое решение "найти ближайший к текущему узлу местоположения и нарисовать прямую линию" не представляется реалистичным. Что делать, если у нас есть ситуация, как на прилагаемой картинке? (UPD)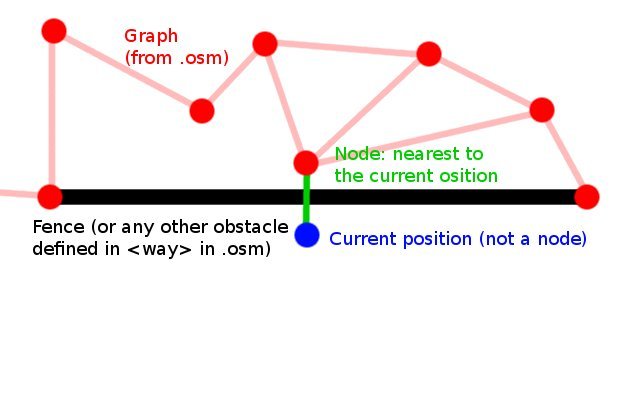
Проблема здесь в том, что перед тем, как мы начнем какие-либо "умные" алгоритмы поиска пути (например, Дейкстры), мы "связываем" текущую позицию с графом, но это просто тупая формула (гипотенуза из теоремы Пифагора) о нахождении ближайшего узла в терминах географические координаты и эта формула не является "путевой" - она не может принимать во внимание препятствия и типы узлов.
Перефразируя это - как нам найти кратчайший путь между A и B, если B является узлом в графе, а A не является узлом?
Вы слышали о каких-либо других решениях этой проблемы?
5 ответов
Процесс, который вы описываете - это " сопоставление карты", и он использует пространственный индекс для поиска ближайшего узла.
Один из распространенных подходов состоит в том, чтобы создать квадродерево, которое содержит все ваши узлы, затем идентифицировать квад, содержащий вашу точку, а затем рассчитать расстояние от вашей точки до всех узлов в квадре (с учетом того, что продольные градусы короче широтных). Если в кваде нет узлов, вы постепенно расширяете свой поиск. Есть несколько предостережений с квадри, но это должно, по крайней мере, помочь вам начать.
На практике я бы просто проигнорировал проблему и использовал предложенный вами алгоритм "прямая линия до ближайшего узла". Пользователь обязан быть как можно ближе к маршрутизируемому объекту. Если первое предположение, которое вы предложили, было ошибочным, пользователь может соответственно изменить начальную позицию.
Пользователь, который действительно начинает свое путешествие по ничейной земле, надеется, что знает покрытую область гораздо больше, чем ваш алгоритм. Доверься ему.
Кстати, это алгоритм, который используют OpenRouteService и Google Maps.
Если все еще не убежден, я предлагаю использовать "самую короткую прямую линию, которая не пересекает препятствие". Если этого все еще недостаточно, определите виртуальную сетку, скажем, 5mx5m и ее диагонали. Чем охватить алгоритм кратчайшего пути до достижения вершины графа.
Вы можете рассматривать текущее местоположение как узел и подключить этот узел к нескольким ближайшим узлам по прямой линии. Приложения GPS будут рассматривать эту прямую линию как "внедорожную", поэтому стоимость этой линии очень велика по сравнению с другими линиями между узлами.
Тем не менее, я не видел вашу прикрепленную фотографию, поэтому не уверен, что это хорошее решение для вас.
Действительно хороший вопрос!
Quad Tree - это решение, так как вы можете индексировать линии / ребра, а не только узлы.
Но проблемы этого "наивного" подхода заключаются в том, что эти решения требуют большого объема памяти. Например, если у вас уже есть очень большой график для вычисления кратчайшего пути, тогда вам нужно столько же или больше памяти для четырехугольного дерева (или я делал что-то очень глупое).
Одно из решений заключается в следующем:
- используйте массив, который является сеткой над используемой областью. Я имею в виду, что вы можете разделить свою область на плитки, и для каждой плитки у вас есть запись массива со списком узлов.
- поэтому для каждой записи массива у вас будет список узлов в этой плитке. Для ребра вы можете просто добавить оба узла в запись. Будьте осторожны, когда есть ребра, пересекающие плитку, не имея своего узла в этой плитке. Алгоритм BresenhamLine поможет здесь.
- Запросы: конвертируйте входные данные ala (lat, lon) в число плиток. Теперь получите все точки из массива. Вычислите ближайшего соседа узлов И ребер до вашей точки A, используя евклидову геометрию (что должно быть хорошо, если они не слишком далеко, как в случае с ближайшим соседом).
Это описание понятно?
Обновление Это теперь реализовано в Graphhopper!
Чтобы получить более эффективное решение для памяти, вы должны просто исключить идентичные узлы для одной записи (плитки).
Немного более сложная техника для уменьшения использования памяти: если при обходе графа учитываются границы тайла, можно представить, что граф затем делится на несколько подграфов для этого тайла (т. Е. Прохождение графа не достигнет другого субграфа). график в пределах плитки). Теперь вам нужны не все узлы, а только узлы, которые лежат в другом подграфе! Это сократит использование памяти, но при запросах вам необходимо пройти не только один край (как в текущей реализации Graphhopper)! Потому что вам нужно пройти всю плитку - т.е. до тех пор, пока границы плитки не будут превышены.
Если у вас есть ограничения на вашем пути, вы должны рассмотреть возможность использования формулировки линейного программирования той же самой задачи кратчайшего пути.
http://en.wikipedia.org/wiki/Shortest_path_problem
Ваша цель будет сводить к минимуму сумму расстояния каждого "пути" между начальным и конечным "узлами", определенными в вашем файле.osm. Любые препятствия будут сформулированы как ограничения. Для реализации с Java, смотрите ссылку ниже.