Требовать, чтобы сплайн был выпуклым

Question

Мне нужно подогнать сплайн к набору данных, а результирующая функция должна быть монотонно убывающей и выпуклой. Данные, которые я передаю в splinefun, гарантированно обладают этими свойствами, но это не гарантирует, что полученная функция является выпуклой. Есть ли способ подогнать сплайн к набору данных и потребовать, чтобы получающаяся функция была выпуклой?

Answer 1

Сначала предоставим пример данных:

x = c(0,1,2,3,4,5,6)
y = c(2,1, 0.59, 0.27, 0.25, -0.23, -0.45)
dat <- data.frame(x=x,y=y)

Монотонный сплайн

Мы можем сделать монотонный сплайн с splinefun(x,y,"monoH.FC") как подсказывает @fang.

# Setting up Monotonic Spline
MonoSpline = splinefun(x,y,"monoH.FC")
#Getting Ready for plotting Monotonic Spline
xArray = seq(0,6,0.01)
MonoResult = MonoSpline(xArray)

Монотонный выпуклый сплайн (с пакетом афера)

Для монотонного выпуклого сплайна необходимо использовать scam пакет. Мы можем тогда:

# Setting up Monotonic Convex Spline
# install.packages("scam")
require(scam)
MonoConvexSpline <- scam(y~s(x,k=4,bs="mdcx",m=1),data=dat)
MonoConvexSplinePredict =function(Test){
  predict.scam(MonoConvexSpline,data.frame(x = Test))
} 
#Getting Ready for plotting Monotonic Convex Spline
MonoConvexSplineResult = MonoConvexSplinePredict(xArray)

Обратите внимание на следующее:

1. Опция bs="mdcx" означает, что мы хотим убывающий выпуклый сплайн. Если вы хотите увеличить выпуклость, уменьшить вогнутость и т. Д., То найдите соответствующий bs значение здесь.
2. Если вы поместите немонтонные данные в splinefun(x,y,"monoH.FC") Функция мы получаем ошибку.
3. Если вы поместите невыпуклые данные в scam функция, то вы все равно получите сплайн. Данные изменяются таким образом, что небольшие выпуклости изменяются на выпуклые. Там нет никаких предупреждений об этом, поэтому будьте осторожны, потому что ваши данные могут выглядеть совершенно иначе. В качестве примера, приведенный ниже график был сделан с использованием того же кода, что и выше, за исключением того, что мы имели bs="mdcv" для убывающей вогнутой функции:

Однотонный выпуклый сплайн (с пакетом початков)

# Convex Cobs Spline
library(cobs)
spCobs = cobs(x , y, constraint = c("decrease", "convex"), nknots = 8)
spCobsResults = predict(spCobs, xArray)[,2] 

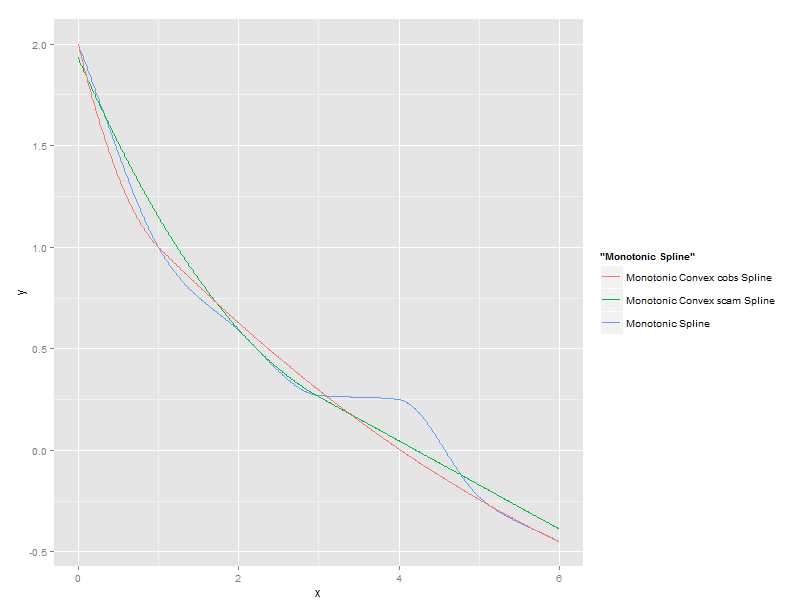
Все

Затем нанесите на карту их

Plot = qplot(xlab = "x", ylab = "y")
Plot = Plot + geom_line(aes(xArray,MonoResult            , colour = "Monotonic Spline"            ))
Plot = Plot + geom_line(aes(xArray,MonoConvexSplineResult, colour = "Monotonic Convex scam Spline"))
Plot = Plot + geom_line(aes(xArray,spCobsResults         , colour = "Monotonic Convex cobs Spline"))
Plot

скорость

• Прогнозирование точек с помощью scam функции, чем с помощью монотонного сплайна или сплайна початков. Вы можете увидеть это из приведенного ниже микробенчмарка
• Сплайн спобов и мошеннических сплайнов требует гораздо больше времени для первоначального расчета, чем общий монотонный сплайн.

,

# Prediction
library(microbenchmark)
    microbenchmark(
      MonoSpline(xArray),
      predict.scam(MonoConvexSpline,data.frame(x = xArray)),
      predict(spCobs, xArray)[,2] 
    )

Unit: microseconds
                                                   expr      min        lq      mean    median        uq      max neval
                                     MonoSpline(xArray)  141.540  147.8175  223.3695  156.9490  167.9830 1593.456   100
 predict.scam(MonoConvexSpline, data.frame(x = xArray)) 2778.655 2838.0095 3161.2282 2914.8665 3153.4285 6168.741   100
                           predict(spCobs, xArray)[, 2]  125.179  133.1690  155.1226  145.1535  162.2755  366.784   100

# Calculating Spline
library(microbenchmark)
microbenchmark(
  splinefun(x,y,"monoH.FC"),
  scam(y~s(x,k=4,bs="mdcx",m=1),data=dat),
  cobs(x , y, constraint = c("decrease", "convex"), nknots = 8) 
)

Unit: microseconds
                                                         expr        min         lq        mean      median         uq       max neval
                                  splinefun(x, y, "monoH.FC")     90.175    127.462    411.6407    153.7155    198.993  24877.47   100
        scam(y ~ s(x, k = 4, bs = "mdcx", m = 1), data = dat) 166769.270 196719.139 231631.5321 224372.7940 265074.525 355734.37   100
 cobs(x, y, constraint = c("decrease", "convex"), nknots = 8) 145511.335 172887.618 203786.0940 202997.4795 228688.607 347661.29   100

Answer 2

Мой другой ответ на этот вопрос показал монотонный сплайн и сплайны, ограниченные по форме початков и афера. Проблема с этими сплайнами с ограниченной формой заключается в том, что они довольно медленные и не обязательно интерполируют все точки данных.

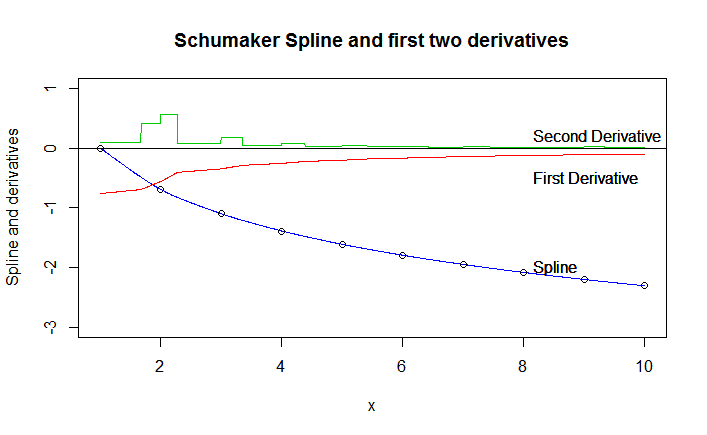
Шумейкер Сплайн

Я выпустил пакет, который реализует сплайн Шумакера, который является монотонным и выпуклым / вогнутым, если данные являются монотонными и выпуклыми / вогнутыми. Это быстро и интерполирует все точки данных.

Для примера:

#install.packages("schumaker")
library(schumaker)

x = seq(1,10)
y = -log(x)
xarray = seq(1,10,0.01)

SchumSpline = schumaker::Schumaker(x,y)
Schum0 = SchumSpline$Spline(xarray)
Schum1 = SchumSpline$DerivativeSpline(xarray)
Schum2 = SchumSpline$SecondDerivativeSpline(xarray)

plot(xarray, Schum0, type = "l", col = 4, ylim = c(-3,1), main = "Schumaker Spline and first two derivatives",
     ylab = "Spline and derivatives", xlab = "x")
points(x,y)
lines(xarray, Schum1, col = 2)
lines(xarray, Schum2, col = 3)
abline(h = 0, col = 1)
text(x=rep(8,8,8), y=c(-2, -0.5,+0.2), pos=4, labels=c('Spline', 'First Derivative', 'Second Derivative'))

Вы можете видеть, что вторая производная всегда положительна (это не верно для нормального монотонного сплайна. См. Виньетка пакета).

Обратите внимание, что сплайн будет глобально выпуклым / вогнутым, только если данные глобально выпуклые / вогнутые. Это неизбежно, так как это интерполирующий сплайн.

Этот сплайн быстрее, чем сплайны из початков и мошенников. Он медленнее, чем монотонный сплайн, но быстрее оценивается. Полный тест скорости можно найти в виньетке.