Моделирование экспоненциального распределения в R

Question

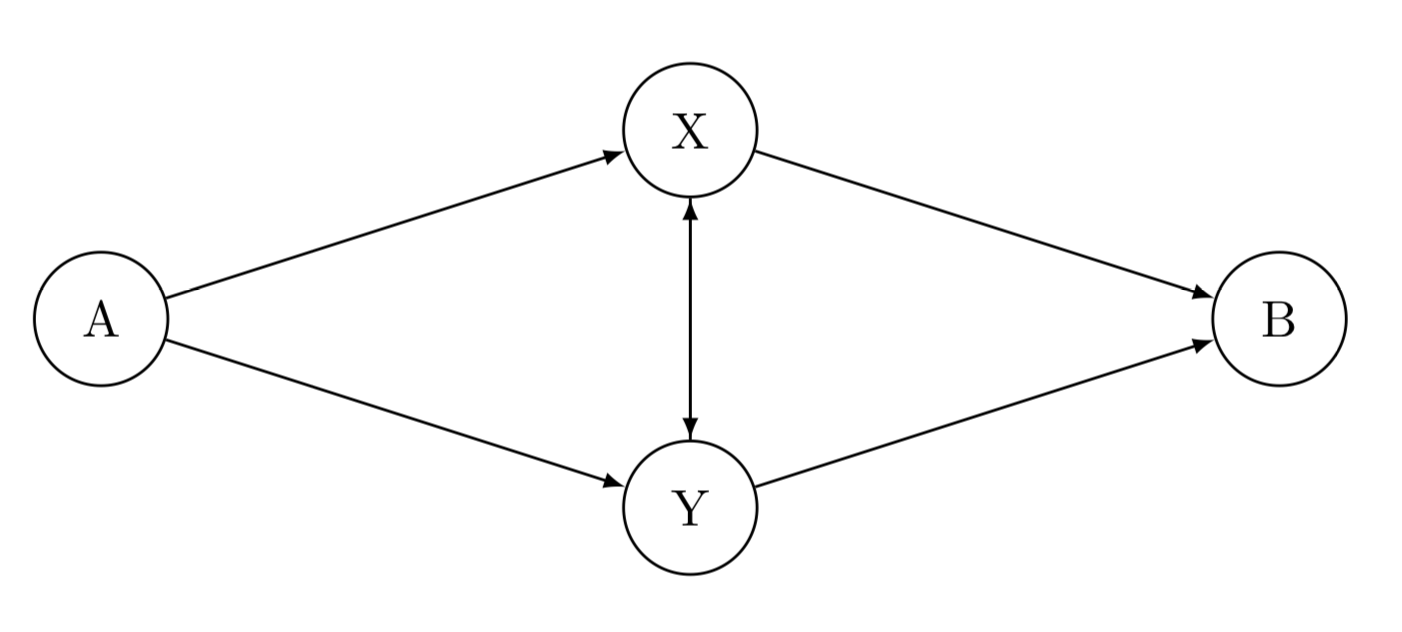
У меня есть следующий график:

Мне сообщили следующую информацию:

(1) вершина A к вершине X описывается экспоненциальным распределением с лямбда = 4;

(2) вершина A к вершине Y описывается экспоненциальным распределением с лямбда = 2.5;

(3) от вершины X до вершины Y, идентичной вершине Y и вершине X, и она описывается экспоненциальным распределением с лямбда = 10;

(4) вершина X к вершине B описывается экспоненциальным распределением с лямбда = 3; и наконец,

(5) вершина Y к вершине B описывается экспоненциальным распределением с лямбда = 5.

Давайте предположим, что я выбираю самый быстрый путь между вершинами в каждой симуляции.

Теперь я хочу узнать среднее время, необходимое для перехода из вершины А в вершину В.

Мой код R выглядит следующим образом:

# Generate/simulate 1000 random numbers for each of the internode paths.

            AtoX <- rexp(1000, 4)
            AtoY <- rexp(1000, 2.5)
            XtoY <- rexp(1000, 10)
            XtoB <- rexp(1000, 3)
            YtoB <- rexp(1000, 5)

    # Length of path from A to X to Y and A to Y to X.

            AYX = AtoY + XtoY
            AXY = AtoX + XtoY

    # Total time of paths from A to B. 

            AXB = AtoX + XtoB
            AYB = AtoY + YtoB
            AXYB = AtoX + XtoY + YtoB
            AYXB = AtoY + XtoY + XtoB

    # Taking the fastest path of all paths. 

            minAXB = min(AXB)
            minAYB = min(AYB)
            minAXYB = min(AXYB)
            minAYXB = min(AYXB)

    # Taking an average of the fastest paths.

            averageTravelTime = 
              mean(minAXB + minAYB + minAXYB + minAYXB)

Это выглядит правильно? Я был бы признателен, если бы люди могли потратить время на проверку моего кода для решения этой проблемы.

Answer 1

1. Это зависит от интерпретации, но я бы сказал, что вам нужно смоделировать время от X до Y и от Y до X отдельно, хотя и с одинаковой скоростью. Если поезд идет в обоих направлениях и в среднем скорость одинакова, это не значит, что два поезда, отправляющиеся из X и Y, прибудут в другую точку одновременно.

2. Вы не используете

   AYX <- AtoY + XtoY
   AXY <- AtoX + XtoY
   

   поэтому они излишни.

3. Пишу minAXB <- min(AXB) на самом деле не имеет смысла. Вы моделируете 1000 раз для каждого края, AXB является вектором 1000 раз маршрута AXB и теперь вы выбираете самый короткий за все время..

4. Так же, averageTravelTime не имеет смысла, потому что minAXB + minAYB + minAXYB + minAYXB это просто число, а не вектор.

Следовательно, я думаю, что код должен быть

set.seed(1)
AtoX <- rexp(1000, 4)
AtoY <- rexp(1000, 2.5)
XtoY <- rexp(1000, 10)
YtoX <- rexp(1000, 10) # added
XtoB <- rexp(1000, 3)
YtoB <- rexp(1000, 5)

AXB <- AtoX + XtoB
AYB <- AtoY + YtoB
AXYB <- AtoX + XtoY + YtoB
AYXB <- AtoY + YtoX + XtoB # changed XtoY to YtoX

TravelTimes <- pmin(AXB, AYB, AXYB, AYXB)
averageTravelTime <- mean(TravelTimes)

Увидеть ?pmin, Для каждого дня он выбирает самое быстрое время в пути и возвращает вектор длины 1000.

В качестве бонуса, следующий показывает, сколько раз, какой маршрут был самым быстрым

table(apply(cbind(AXB, AYB, AXYB, AYXB), 1, which.min))
#   1   2   3   4 
# 317 370 240  73