Эффективная структура данных или метод для управления данными построения, которые растут со временем
Я хотел бы спросить, является ли следующий способ управления результатом построения графиков эффективным использованием Mathematica и есть ли более "функциональный" способ сделать это. (может использовать Соу, Рип и тому подобное).
Проблема основная. Предположим, вы хотите смоделировать физический процесс, скажем, маятник, и хотите построить график временных рядов решения (т.е. время в зависимости от угла) по мере его выполнения (или любой другой тип результата).
Чтобы показать график, нужно сохранять точки данных во время работы.
Ниже приведен простой пример, который отображает решение, но только текущую точку, а не полный временной ряд:
Manipulate[
sol = First@NDSolve[{y''[t] + 0.1 y'[t] + Sin[y[t]] == 0, y[0] == Pi/4, y'[0] == 0},
y, {t, time, time + 1}];
With[{angle = y /. sol},
(
ListPlot[{{time, angle[time]}}, AxesLabel -> {"time", "angle"},
PlotRange -> {{0, max}, {-Pi, Pi}}]
)
],
{{time, 0, "run"}, 0, max, Dynamic@delT, ControlType -> Trigger},
{{delT, 0.1, "delT"}, 0.1, 1, 0.1, Appearance -> "Labeled"},
TrackedSymbols :> {time},
Initialization :> (max = 10)
]
Вышесказанное не интересно, так как видна только движущаяся точка, а не полный путь решения.
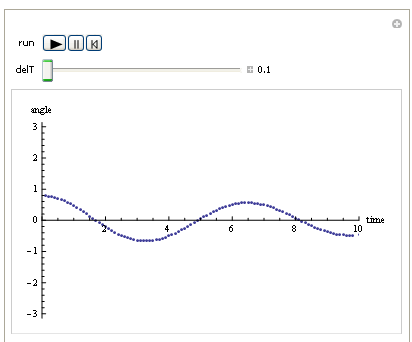
Способ, которым я в настоящее время занимаюсь, это выделить, используя Table[]буфер, достаточно большой для хранения максимально возможного размера временного ряда, который может быть сгенерирован.
Проблема в том, что временной шаг может измениться, и чем он меньше, тем больше данных будет сгенерировано.
Но так как я знаю наименьший возможный временной шаг (который в этом примере составляет 0,1 секунды), и я знаю общее время выполнения (которое здесь составляет 10 секунд), то я знаю, сколько выделить.
Мне также нужен индекс для отслеживания буфера. Используя этот метод, вот способ сделать это:
Manipulate[
If[time == 0, index = 0];
sol = First@NDSolve[{y''[t] + 0.1 y'[t] + Sin[y[t]] == 0, y[0] == Pi/4,y'[0] == 0},
y, {t, time, time + 1}];
With[{angle = y /. sol},
(
index += 1;
buffer[[index]] = {time, angle[time]};
ListPlot[buffer[[1 ;; index]], Joined -> True, AxesLabel -> {"time", "angle"},
PlotRange -> {{0, 10}, {-Pi, Pi}}]
)
],
{{time, 0, "run"}, 0, 10, Dynamic@delT, AnimationRate -> 1, ControlType -> Trigger},
{{delT, 0.1, "delT"}, 0.1, 1, 0.1, Appearance -> "Labeled"},
{{buffer, Table[{0, 0}, {(max + 1)*10}]}, None},
{{index, 0}, None},
TrackedSymbols :> {time},
Initialization :> (max = 10)
]
Для справки, когда я делаю что-то подобное в Matlab, у него есть хорошая возможность для построения графиков, которая называется "держись". Чтобы можно было построить точку, а затем сказать "держись", это означает, что следующий график не сотрет то, что уже есть на графике, а добавит его.
Я не нашел что-то подобное в Mathematica, то есть обновлять текущий сюжет на лету.
Я также не хотел использовать Append[] и AppendTo[] для создания буфера во время его работы, так как это будет медленно и неэффективно.
Мой вопрос: есть ли более эффективный, Mathematica способ (который может быть быстрее и удобнее) для выполнения типичной задачи, такой как описанная выше, кроме того, что я делаю?
Спасибо,
ОБНОВИТЬ:
На вопрос, почему не решить ODE все сразу. Да, это возможно, но это сильно упрощает задачу по частям, в том числе по соображениям производительности. Вот пример с одой с начальными условиями:
Manipulate[
If[time == 0, index = 0];
sol = First@
NDSolve[{y''[t] + 0.1 y'[t] + Sin[y[t]] == 0, y[0] == y0,
y'[0] == yder0}, y, {t, time, time + 1}];
With[{angle = (y /. sol)[time]},
(
index += 1;
buffer[[index]] = {time, angle};
ListPlot[buffer[[1 ;; index]], Joined -> True,
AxesLabel -> {"time", "angle"},
PlotRange -> {{0, 10}, {-Pi, Pi}}])],
{{time, 0, "run"}, 0, 10, Dynamic@delT, AnimationRate -> 1,
ControlType -> Trigger}, {{delT, 0.1, "delT"}, 0.1, 1, 0.1,
Appearance -> "Labeled"},
{{y0, Pi/4, "y(0)"}, -Pi, Pi, Pi/100, Appearance -> "Labeled"},
{{yder0, 0, "y'(0)"}, -1, 1, .1, Appearance -> "Labeled"},
{{buffer, Table[{0, 0}, {(max + 1)*10}]}, None},
{{index, 0}, None},
TrackedSymbols :> {time},
Initialization :> (max = 10)
]

Теперь, когда нужно было решить систему однажды, им нужно следить за тем, не изменится ли IC. Это может быть сделано, но нужна дополнительная логика, и я делал это раньше много раз, но это немного усложняет ситуацию. Я написал небольшую заметку по этому вопросу здесь.
Кроме того, я заметил, что я могу получить намного лучшую скорость, решая систему для меньших временных отрезков с течением времени, чем все это сразу. Затраты на вызов NDSolve очень малы. Но когда длительность времени для NDsolve для велика, могут возникнуть проблемы, когда кто-то запросит более высокую точность от NDSolve, как в опциях AccuracyGoal ->, PrecisionGoal ->, что я не мог, когда временной интервал очень большой.
В целом издержки вызова NDSolve для небольших сегментов, по-видимому, намного меньше по сравнению с преимуществами, которые он дает в упрощении логики и скорости (может быть, более точными, но я больше не проверял это). Я знаю, что немного странно продолжать вызывать NDSolve, но после попытки обоих методов (все сразу, но добавить логику для проверки других управляющих переменных) по сравнению с этим методом, я теперь склоняюсь к этому.
ОБНОВЛЕНИЕ 2
Я сравнил следующие 4 метода для 2 тестовых случаев:
tangle [j][j] метод (Велизарий)
AppendTo (предложено Шьордом) Динамический связанный список (Леонид) (с и без SetAttributes[linkedList, HoldAllComplete]) предварительно выделить буфер (Насер)
Я сделал это, выполнив 2 случая: один на 10 000 баллов, а второй на 20 000 баллов. Я оставил там команду Plot[[], но не отображаю ее на экране, это исключает любые накладные расходы на фактический рендеринг.
Я использовал Timing[] вокруг цикла Do, который перебирает основную логику, которая называется NDSolve, и перебирает временной интервал с использованием приращений delT, как описано выше. Манипуляции не использовались.
Я использовал Quit[] перед каждым запуском.
Для метода Леонида я изменил столбец [], который он имел в цикле Do. В конце я проверил, но вычерчивал данные, используя его метод getData[], что результат в порядке.
Весь код, который я использовал ниже. Я сделал таблицу, которая показывает результаты для 10000 баллов и 20000. Время в секундах:
result = Grid[{
{Text[Style["method", Bold]],
Text[Style["number of elements", Bold]], SpanFromLeft},
{"", 10000, 20000},
{"", SpanFromLeft},
{"buffer", 129, 571},
{"AppendTo", 128, 574},
{"tangle[j][j]", 612, 2459},
{"linkedList with SetAttribute", 25, 81},
{"linkedList w/o SetAttribute", 27, 90}}
]

Понятно, что если я не сделал что-то не так, но ниже приведен код, который может проверить каждый, метод Леонида легко выигрывает. Я также был удивлен, что AppendTo сделал так же хорошо, как метод буфера, который предварительно выделял данные.
Вот слегка измененный код, который я использовал для генерации вышеуказанных результатов.
буферный метод
delT = 0.01; max = 100; index = 0;
buffer = Table[{0, 0}, {(max + 1)*1/delT}];
Timing[
Do[
sol = First@
NDSolve[{y''[t] + 0.1 y'[t] + Sin[y[t]] == 0, y[0] == Pi/4,
y'[0] == 0}, y, {t, time, time + 1}];
With[{angle = y /. sol},
(index += 1;
buffer[[index]] = {time, angle[time]};
foo =
ListPlot[buffer[[1 ;; index]], Joined -> True,
AxesLabel -> {"time", "angle"},
PlotRange -> {{0, 10}, {-Pi, Pi}}]
)
], {time, 0, max, delT}
]
]
Метод AppendTo
Clear[y, t];
delT = 0.01; max = 200;
buffer = {{0, 0}}; (*just a hack to get ball rolling, would not do this in real code*)
Timing[
Do[
sol = First@
NDSolve[{y''[t] + 0.1 y'[t] + Sin[y[t]] == 0, y[0] == Pi/4,
y'[0] == 0}, y, {t, time, time + 1}];
With[{angle = y /. sol},
(AppendTo[buffer, {time, angle[time]}];
foo =
ListPlot[buffer, Joined -> True, AxesLabel -> {"time", "angle"},
PlotRange -> {{0, 10}, {-Pi, Pi}}]
)
], {time, 0, max, delT}
]
]
метод путаницы [j][j]
Clear[y, t];
delT = 0.01; max = 200;
Timing[
Do[
sol = First@
NDSolve[{y''[t] + 0.1 y'[t] + Sin[y[t]] == 0, y[0] == Pi/4,
y'[0] == 0}, y, {t, time, time + 1}];
tangle[time] = y /. sol;
foo = ListPlot[
Table[{j, tangle[j][j]}, {j, .1, max, delT}],
AxesLabel -> {"time", "angle"},
PlotRange -> {{0, max}, {-Pi, Pi}}
]
, {time, 0, max, delT}
]
]
метод динамического связанного списка
Timing[
max = 200;
ClearAll[linkedList, toLinkedList, fromLinkedList, addToList, pop,
emptyList];
SetAttributes[linkedList, HoldAllComplete];
toLinkedList[data_List] := Fold[linkedList, linkedList[], data];
fromLinkedList[ll_linkedList] :=
List @@ Flatten[ll, Infinity, linkedList];
addToList[ll_, value_] := linkedList[ll, value];
pop[ll_] := Last@ll;
emptyList[] := linkedList[];
Clear[getData];
Module[{ll = emptyList[], time = 0, restart, plot, y},
getData[] := fromLinkedList[ll];
plot[] := Graphics[
{
Hue[0.67`, 0.6`, 0.6`],
Line[fromLinkedList[ll]]
},
AspectRatio -> 1/GoldenRatio,
Axes -> True,
AxesLabel -> {"time", "angle"},
PlotRange -> {{0, 10}, {-Pi, Pi}},
PlotRangeClipping -> True
];
DynamicModule[{sol, angle, llaux, delT = 0.01},
restart[] := (time = 0; llaux = emptyList[]);
llaux = ll;
sol :=
First@NDSolve[{y''[t] + 0.1 y'[t] + Sin[y[t]] == 0, y[0] == Pi/4,
y'[0] == 0}, y, {t, time, time + 1}];
angle := y /. sol;
ll := With[{res =
If[llaux === emptyList[] || pop[llaux][[1]] != time,
addToList[llaux, {time, angle[time]}],
(*else*)llaux]
},
llaux = res
];
Do[
time += delT;
plot[]
, {i, 0, max, delT}
]
]
]
]
спасибо всем за помощь.
3 ответа
Я не знаю, как получить то, что вы хотите с Manipulate, но мне, кажется, удалось получить что-то близкое с обычаем Dynamic, Следующий код будет: использовать связанные списки, чтобы быть достаточно эффективными, останавливать / возобновлять ваш график с помощью кнопки, и собирать данные, доступные на данный момент, по запросу в любой момент времени:
ClearAll[linkedList, toLinkedList, fromLinkedList, addToList, pop, emptyList];
SetAttributes[linkedList, HoldAllComplete];
toLinkedList[data_List] := Fold[linkedList, linkedList[], data];
fromLinkedList[ll_linkedList] := List @@ Flatten[ll, Infinity, linkedList];
addToList[ll_, value_] := linkedList[ll, value];
pop[ll_] := Last@ll;
emptyList[] := linkedList[];
Clear[getData];
Module[{ll = emptyList[], time = 0, restart, plot, y},
getData[] := fromLinkedList[ll];
plot[] :=
Graphics[{Hue[0.67`, 0.6`, 0.6`], Line[fromLinkedList[ll]]},
AspectRatio -> 1/GoldenRatio, Axes -> True,
AxesLabel -> {"time", "angle"}, PlotRange -> {{0, 10}, {-Pi, Pi}},
PlotRangeClipping -> True];
DynamicModule[{sol, angle, llaux, delT = 0.1},
restart[] := (time = 0; llaux = emptyList[]);
llaux = ll;
sol := First@
NDSolve[{y''[t] + 0.1 y'[t] + Sin[y[t]] == 0, y[0] == Pi/4, y'[0] == 0},
y, {t, time, time + 1}];
angle := y /. sol;
ll := With[{res =
If[llaux === emptyList[] || pop[llaux][[1]] != time,
addToList[llaux, {time, angle[time]}],
(* else *)
llaux]},
llaux = res];
Column[{
Row[{Dynamic@delT, Slider[Dynamic[delT], {0.1, 1., 0.1}]}],
Dynamic[time, {None, Automatic, None}],
Row[{
Trigger[Dynamic[time], {0, 10, Dynamic@delT},
AppearanceElements -> { "PlayPauseButton"}],
Button[Style["Restart", Small], restart[]]
}],
Dynamic[plot[]]
}, Frame -> True]
]
]
Связанные списки здесь заменяют ваши buffer и вам не нужно заранее выделять и заранее знать, сколько точек данных у вас будет. plot[] пользовательская функция построения графиков низкого уровня, хотя мы, вероятно, могли бы также ListPlot, Вы используете кнопку "Play" для остановки и возобновления печати, а также пользовательскую кнопку "Restart" для сброса параметров.
Ты можешь позвонить getData[] в любой момент времени получить список данных, накопленных до сих пор, например:
In[218]:= getData[]
Out[218]= {{0,0.785398},{0.2,0.771383},{0.3,0.754062},{0.4,0.730105},{0.5,0.699755},
{0.6,0.663304},{0.7,0.621093},{0.8,0.573517},{0.9,0.521021},{1.,0.464099},
{1.1,0.403294},{1.2,0.339193},{1.3,0.272424}}
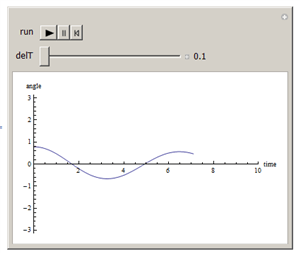
Мне просто интересно, почему вы хотите решить DE по частям. Это может быть решено для всего интервала сразу. Также нет необходимости размещать NDSolve в Манипулировать тогда. Это не должно быть решено снова и снова, когда тело Manipulateсрабатывает. Plot само по себе достаточно быстро, чтобы построить растущий график на каждом временном шаге. Следующий код делает то, что вы хотите без необходимости хранения.
sol = First@
NDSolve[{y''[t] + 0.1 y'[t] + Sin[y[t]]==0,y[0] == Pi/4,y'[0] == 0}, y, {t, 0, 10}];
eps = 0.000001;
Manipulate[
With[{angle = y /. sol},
Plot[angle[t], {t, 0, time + eps},
AxesLabel -> {"time", "angle"},
PlotRange -> {{0, max}, {-Pi, Pi}}
]
],
{{time, 0, "run"}, 0, max,Dynamic@delT, ControlType -> Trigger},
{{delT, 0.1, "delT"}, 0.1, 1, 0.1, Appearance -> "Labeled"}, TrackedSymbols :> {time},
Initialization :> (max = 10)
]
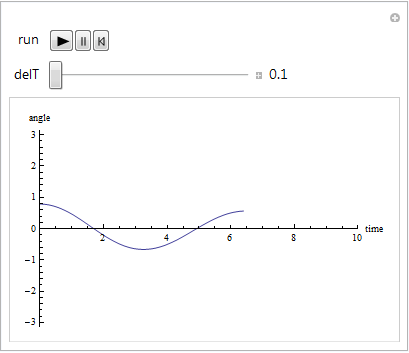
Кстати: AppendTo может быть засекречен как медленный, но это не так медленно. В типичном списке, подходящем для построения графика, это занимает менее миллисекунды, поэтому оно не должно вообще замедляться.
Совсем не эффективно с точки зрения памяти, но его преимущество в том, что ему требуется лишь небольшая модификация вашего первого кода:
Clear[tangle];
Manipulate[
sol = First@NDSolve[{y''[t] + 0.1 y'[t] + Sin[y[t]] == 0,
y[0] == Pi/4,
y'[0] == 0},
y, {t, time, time + 1}];
(tangle[time] = y /. sol;
ListPlot[Table[{j, tangle[j][j]}, {j, .1, max, delT}],
AxesLabel -> {"time", "angle"},
PlotRange -> {{0, max}, {-Pi, Pi}}]),
{{time, 0, "run"}, 0, max, Dynamic@delT, ControlType -> Trigger},
{{delT, 0.1, "delT"}, 0.1, 1, 0.1, Appearance -> "Labeled"},
TrackedSymbols :> {time},
Initialization :> {(max = 10); i = 0}]