Обрабатывает ли преобразование Фурье только периодический сигнал?
Апериодический сигнал может быть обработан с помощью DFT. DFT может обрабатывать как периодический, так и апериодический сигнал?
2 ответа
Дискретное преобразование Фурье (DFT) определяет взаимосвязь между N-точечной последовательностью во временной области x[n], n=0..N-1 и N-точечной последовательностью в частотной области (выборки преобразования Фурье, равномерно распределенные между \omega = 0 и 2\pi) X[k], k=0..N-1. Прямое преобразование дается:
X[k] = 1/N \sum_{n=0}^{N-1} x[n] exp{-j 2\pi k.n/N}
который может быть выражен как матричное умножение
X = D x
где x и X - N-элементные векторы столбцов, соответствующие временной и частотной областям, и D - матрица DFT размером N × N,
D_{kn} = 1/N exp{-j 2\pi k.n/N}
(и, таким образом, обратное преобразование тривиально выводится из матрицы, обратной D).
Таким образом, вы можете вычислить X [k] для любой N-точечной входной последовательности x [n], и даже не имеет особого смысла определять периодичность для последовательности конечной длины. Если x [n] можно разбить на несколько частей, которые точно повторяются (например, повторяющаяся N/2-точечная последовательность), то мы увидим соответствующую структуру в X[k] (все нечетные спектральные выборки будут равны нулю для этого пример).
Теперь вы можете интерпретировать ДПФ как преобразование Фурье периодической последовательности бесконечной длительности, состоящей из бесконечного числа повторов последовательности N-точечной временной области, с которой вы начинаете. В этом случае значения ДПФ X [k] соответствуют весам дельт Дирака, которые составляют спектр этой бесконечной энергии (но конечной степени) последовательности.
Но вы также можете интерпретировать это как выборку преобразования Фурье последовательности конечной длины, эквивалентно последовательности бесконечной продолжительности, которая оказывается ненулевой только в конечном N-точечном диапазоне. В этом случае значения X [k] являются конечными выборками полного непрерывного частотного преобразования Фурье.
Да, ты можешь. Хорошее объяснение сделано здесь. ( http://www.swarthmore.edu/NatSci/echeeve1/Class/e12/Lectures/FourierXform/FourierXFormI.html)
Кажется, что периодическая функция не имела бы преобразования Фурье, потому что она нарушает первый из критериев сходимости. Однако, если мы учтем импульсные функции, мы сможем обойти это ограничение (это позволит нам использовать преобразования Фурье как для периодических, так и для апериодических функций).
Рассмотрим функцию в частотной области, которая представляет собой простой импульс, масштабированный на 2p (коэффициент масштабирования будет удобен чуть позже).
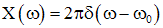
Мы можем найти соответствующую функцию во временной области, вычислив обратное преобразование Фурье,
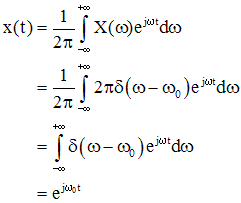
(Последний шаг был выполнен с использованием свойства просеивания импульсной функции.) Обратите внимание, что функция временной области, x(t), является периодической. Поэтому, если мы допустим импульсы в области Фурье, мы можем иметь периодические функции во временной области. Это был особый случай, но мы можем представить любую (с учетом критериев сходимости, например, для ряда Фурье) периодическую функцию с помощью преобразования Фурье. Сначала рассмотрим преобразование Фурье, представляющее собой бесконечную сумму импульсов (это придумано, но упрощается до чего-то полезного).
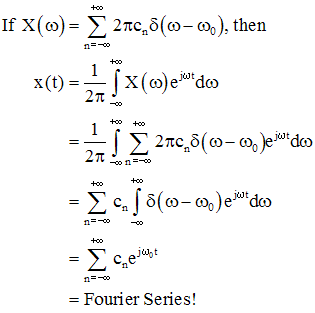
(Этот вывод также использует свойство просеивания.) Итак, чтобы найти преобразование Фурье периодического сигнала x (t), сначала найдите коэффициенты ряда Фурье cn, затем