Куча против бинарного дерева поиска (BST)
В чем разница между кучей и BST?
Когда использовать кучу, а когда использовать BST?
Если вы хотите получить элементы в отсортированном виде, лучше ли BST по сравнению с кучей?
9 ответов
Резюме
Type BST (*) Heap
Insert average log(n) 1
Insert worst log(n) log(n) or n (***)
Find any worst log(n) n
Find max worst 1 (**) 1
Create worst n log(n) n
Delete worst log(n) log(n)
Все средние значения времени в этой таблице совпадают с их худшими значениями времени, за исключением вставки.
*: везде в этом ответе BST == Сбалансированный BST, так как неуравновешенный отстой асимптотически**: используя тривиальную модификацию, объясненную в этом ответе***:log(n)для кучи указателя дерева,nдля динамического массива кучи
Преимущества двоичной кучи по сравнению с BST
среднее время вставки в двоичную кучу
O(1)для BST естьO(log(n)), Это убийственная особенность куч.Есть и другие кучи, которые достигают
O(1)амортизируются (сильнее), как куча Фибоначчи, и даже в худшем случае, как очередь Бродала, хотя они могут быть непрактичными из-за неасимптотической производительности: где-нибудь на практике используются кучи Фибоначчи или очереди Бродала?двоичные кучи могут быть эффективно реализованы поверх динамических массивов или основанных на указателях деревьев, BST - только основанных на указателях деревьев. Таким образом, для кучи мы можем выбрать более компактную реализацию массива, если мы можем позволить себе время от времени изменять размеры.
создание двоичной кучи
O(n)худший случай,O(n log(n))для BST.
Преимущество BST перед двоичной кучей
поиск произвольных элементов
O(log(n)), Это убийственная особенность BST.Для кучи это
O(n)в общем, за исключением самого большого элемента, которыйO(1),
"Ложное" преимущество кучи перед BST
куча это
O(1)найти максимум, BSTO(log(n)),Это распространенное заблуждение, потому что тривиально модифицировать BST для отслеживания самого большого элемента и обновлять его всякий раз, когда этот элемент может быть изменен: при вставке большего свопа, при удалении найдите второе по величине. Можем ли мы использовать двоичное дерево поиска для симуляции работы кучи? (упомянуто Йео).
На самом деле, это ограничение кучи по сравнению с BST: единственный эффективный поиск - поиск самого большого элемента.
Средняя двоичная куча вставки O(1)
Источники:
- Документ: http://i.stanford.edu/pub/cstr/reports/cs/tr/74/460/CS-TR-74-460.pdf
- Слайды WSU: http://www.eecs.wsu.edu/~holder/courses/CptS223/spr09/slides/heaps.pdf
Интуитивный аргумент:
- нижние уровни дерева имеют экспоненциально больше элементов, чем верхние уровни, поэтому новые элементы почти наверняка будут идти внизу
- вставка кучи начинается снизу, BST должна начинаться сверху
В двоичной куче увеличение значения по данному индексу также O(1) по той же причине. Но если вы хотите это сделать, вполне вероятно, что вы захотите поддерживать дополнительный индекс в актуальном состоянии для операций с кучей. Как реализовать операцию уменьшения ключа O(logn) для приоритетной очереди на основе минимальной кучи? например, для Дейкстры. Возможно без дополнительных затрат времени.
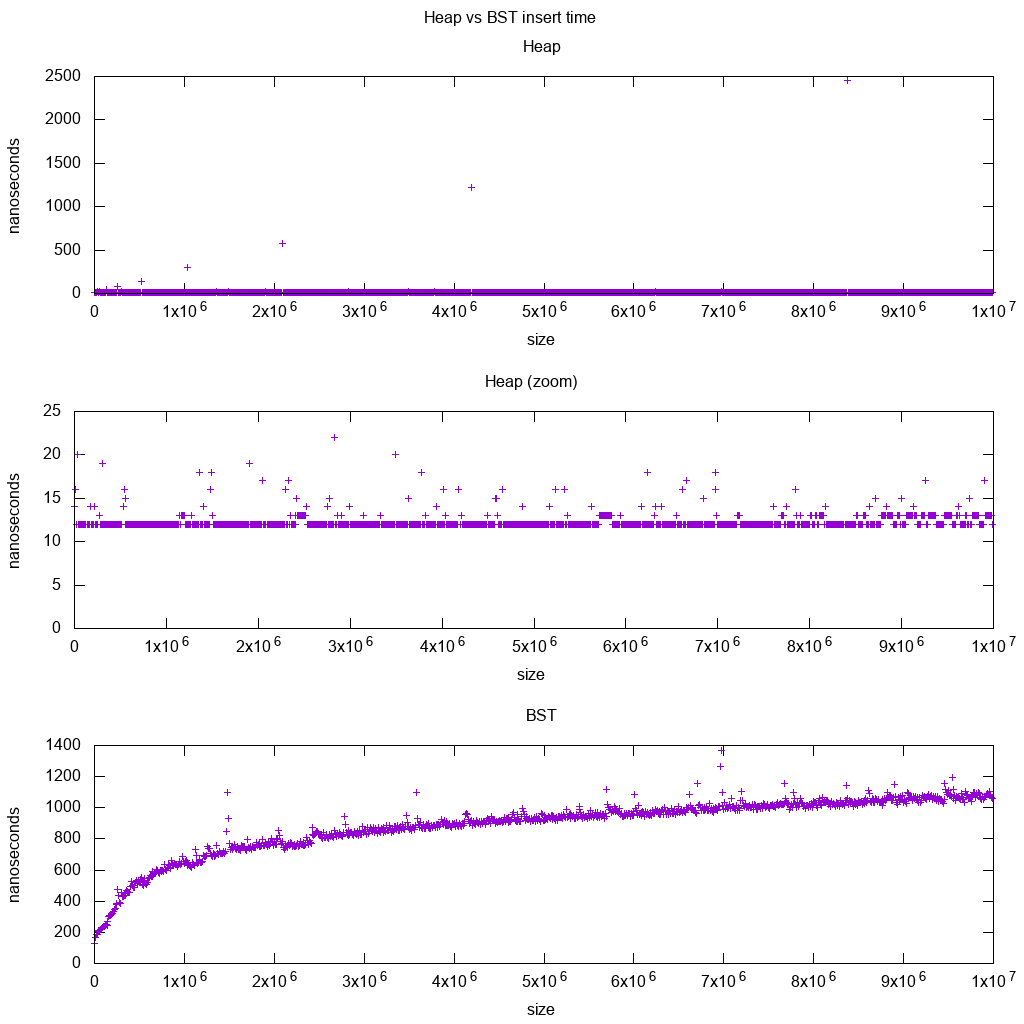
Стандарт вставки стандартной библиотеки GCC C++ на реальном оборудовании
Я тестировал C++ std::set ( Красно-чёрное дерево BST) и std::priority_queue ( динамическая куча массива) вставка с этим кодом и сценарием построения, чтобы увидеть, был ли я прав насчет времени вставки, и вот что я получил:
Так ясно:
Время вставки кучи в основном постоянно.
Мы ясно видим точки изменения размера динамического массива. Поскольку мы усредняем каждые 10 тыс. Вставок , чтобы увидеть что-либо выше системного шума, эти пики на самом деле примерно в 10 тыс. Раз больше, чем показано!
Увеличенный график исключает, по существу, только точки изменения размера массива и показывает, что почти все вставки не достигают 25 наносекунд.
BST является логарифмическим. Все вставки намного медленнее, чем вставка средней кучи.
Ubuntu 18.04, GCC 7.3, процессор Intel i7-7820HQ, оперативная память DDR4 2400 МГц, Lenovo Thinkpad P51.
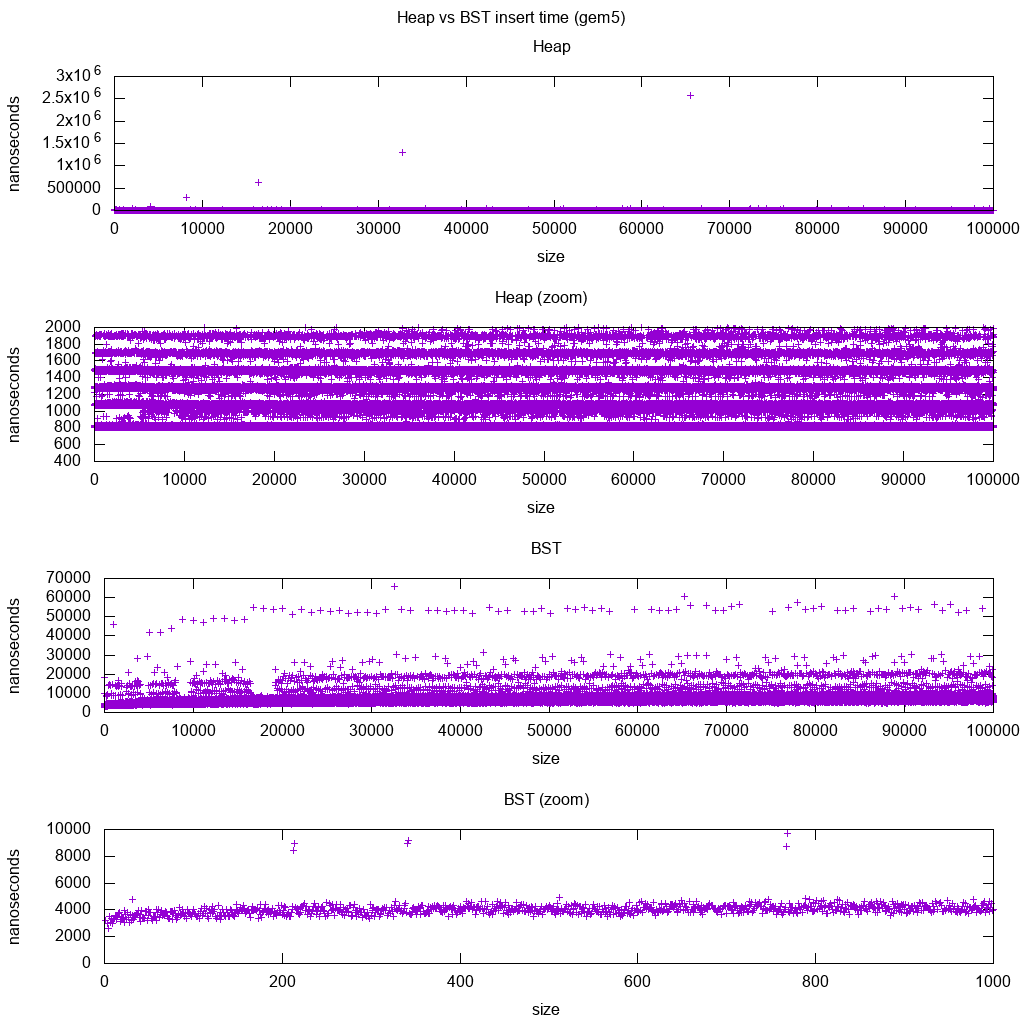
Стандарт вставки стандартной библиотеки GCC C++ для gem5
gem5 - это симулятор полной системы, поэтому он обеспечивает бесконечно точные часы с m5 dumpstats, Поэтому я попытался использовать его для оценки времени для отдельных вставок.
Интерпретация:
куча все еще постоянна, но теперь мы видим более подробно, что есть несколько строк, и каждая более высокая строка является более разреженной.
Это должно соответствовать задержкам доступа к памяти, которые выполняются для более высоких и более высоких вставок.
TODO Я не могу толковать BST полностью, поскольку он не выглядит таким логарифмическим и несколько более постоянным.
Однако с помощью этой более подробной детализации мы можем видеть также несколько отдельных линий, но я не уверен, что они представляют: я ожидаю, что нижняя линия будет тоньше, так как мы вставляем верхний низ?
Сравнительный анализ с этой установкой Buildroot на процессоре HPI aarch64.
BST не может быть эффективно реализован в массиве
Операции с кучей должны только пузыриться вверх или вниз по одной ветви дерева, поэтому O(log(n)) в худшем случае, O(1) средний.
Сохранение баланса BST требует поворотов дерева, которые могут изменить верхний элемент на другой, и потребует перемещения всего массива (O(n)).
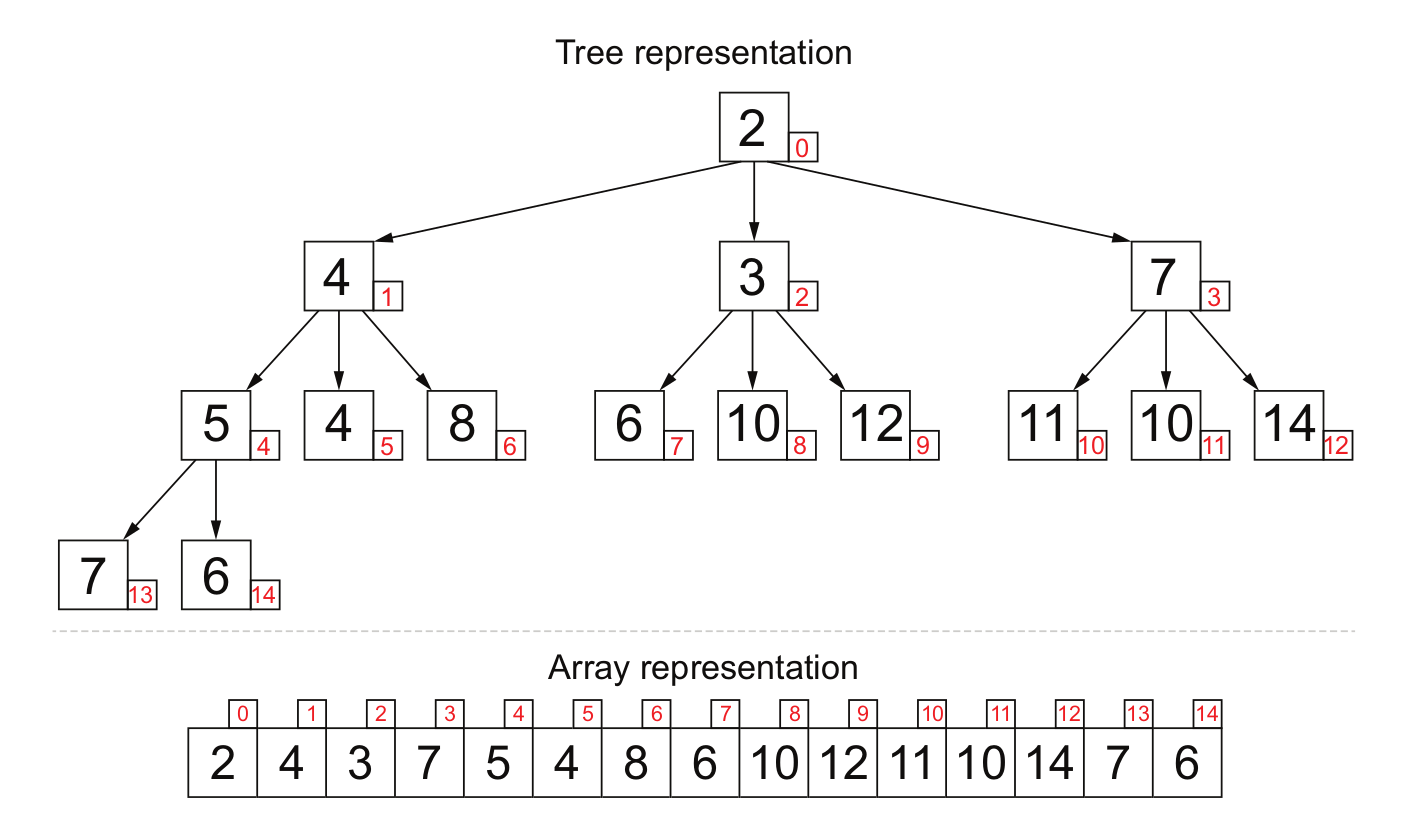
Кучи могут быть эффективно реализованы в массиве
Родительские и дочерние индексы могут быть вычислены из текущего индекса, как показано здесь.
Там нет операций балансировки, как BST.
Удалить мин - самая тревожная операция, так как она должна быть сверху вниз. Но это всегда можно сделать, "перколируя" одну ветвь кучи, как описано здесь. Это приводит к наихудшему случаю O(log(n)), поскольку куча всегда хорошо сбалансирована.
Если вы вставляете по одному узлу для каждого удаляемого вами, то вы теряете преимущество асимптотической средней (1) вставки, которую обеспечивают кучи, так как удаление будет доминировать, и вы также можете использовать BST. Dijkstra, однако, обновляет узлы несколько раз для каждого удаления, так что мы в порядке.
Динамические массивы кучи против куч дерева указателей
Кучи могут быть эффективно реализованы поверх кучи указателей: возможно ли сделать эффективные реализации двоичной кучи на основе указателей?
Реализация динамического массива более экономична. Предположим, что каждый элемент кучи содержит только указатель на struct:
реализация дерева должна хранить три указателя для каждого элемента: parent, left child и right child. Так что использование памяти всегда
4n(3 указателя дерева + 1structуказатель).Древовидным BST также потребуется дополнительная информация о балансировке, например, черно-красная.
реализация динамического массива может иметь размер
2nтолько после удвоения. Так что в среднем это будет1.5n,
С другой стороны, в куче дерева лучше вставка в худшем случае, потому что копирование динамического массива резервных копий для удвоения его размера занимает O(n) наихудший случай, в то время как куча дерева просто делает новые небольшие выделения для каждого узла.
Тем не менее, дублирование массива O(1) амортизируется, поэтому сводится к рассмотрению максимальной задержки. Упоминается здесь.
философия
BST поддерживают глобальное свойство между родителем и всеми потомками (слева меньше, справа больше).
Верхний узел BST является средним элементом, который требует глобальных знаний для поддержания (знание количества меньших и больших элементов).
Это глобальное свойство более дорогое в обслуживании (log n insert), но дает более мощный поиск (log n search).
Кучи поддерживают локальное свойство между родительским и прямым потомками (parent > children).
Верхняя нота кучи - это большой элемент, который требует только локальных знаний (знание вашего родителя).
Двусвязный список
Двусвязный список можно рассматривать как подмножество кучи, где первый элемент имеет наибольший приоритет, поэтому давайте сравним их и здесь:
- вставка:
- позиция:
- двусвязный список: вставленный элемент должен быть первым или последним, поскольку у нас есть только указатели на эти элементы.
- двоичная куча: вставленный элемент может оказаться в любой позиции. Менее ограниченный, чем связанный список.
- время:
- двусвязный список:
O(1)худший случай, так как у нас есть указатели на элементы, а обновление действительно простое - двоичная куча:
O(1)средний, таким образом, хуже, чем связанный список. Компромисс для более общей позиции вставки.
- двусвязный список:
- позиция:
- поиск:
O(n)для обоих
Вариант использования этого - случай, когда ключом кучи является текущая временная метка: в этом случае новые записи всегда будут идти в начало списка. Таким образом, мы можем даже забыть точную метку времени и просто сохранить позицию в списке в качестве приоритета.
Это может быть использовано для реализации кэша LRU. Как и в случае с кучными приложениями, такими как Dijkstra, вы захотите сохранить дополнительную хэш-карту от ключа к соответствующему узлу списка, чтобы быстро найти какой узел обновлять.
BST против хэш-карты
Несколько хороших графиков: Какая структура данных находится внутри std::map в C++?
Смотрите также
Аналогичный вопрос по CS: https://cs.stackexchange.com/questions/27860/whats-the-difference-between-a-binary-search-tree-and-a-binary-heap
Куча просто гарантирует, что элементы на более высоких уровнях больше (для max-heap) или меньше (для min-heap), чем элементы на более низких уровнях, тогда как BST гарантирует порядок (от "левого" к "правому"). Если вы хотите отсортированные элементы, используйте BST.
Когда использовать кучу, а когда использовать BST
Куча лучше в findMin/findMax (O(1)) пока BST хороша на все находки (O(logN)). Вставить O(logN) для обеих структур. Если вы заботитесь только о findMin/findMax (например, о приоритетах), переходите к куче. Если вы хотите, чтобы все было отсортировано, используйте BST.
Первые несколько слайдов здесь объясняют вещи очень четко.
Как уже упоминалось, куча может сделать findMin или же findMax в O(1), но не оба в одной структуре данных. Однако я не согласен с тем, что Heap лучше в findMin / findMax. На самом деле, с небольшой модификацией, BST может сделать как findMin а также findMax в O(1).
В этом модифицированном BST вы отслеживаете узел min и узел max каждый раз, когда выполняете операцию, которая потенциально может изменить структуру данных. Например, в операции вставки вы можете проверить, больше ли минимальное значение, чем вновь вставленное значение, а затем назначить минимальное значение вновь добавленному узлу. Та же самая техника может быть применена к максимальному значению. Следовательно, этот BST содержит эту информацию, которую вы можете получить в O(1). (так же, как двоичная куча)
В этом BST (Сбалансированный BST), когда вы pop min или же pop maxследующее минимальное значение, которое должно быть назначено, является преемником минимального узла, тогда как следующее максимальное значение, которое должно быть назначено, является предшественником максимального узла. Таким образом, он выполняет в O(1). Однако нам нужно перебалансировать дерево, поэтому оно все равно будет работать O(log n). (так же, как двоичная куча)
Мне было бы интересно услышать вашу мысль в комментарии ниже. Спасибо:)
Обновить
Перекрестная ссылка на похожий вопрос. Можем ли мы использовать двоичное дерево поиска для имитации операции с кучей? для дальнейшего обсуждения по моделированию кучи с использованием BST.
Бинарное дерево поиска использует определение: для каждого узла узел слева от него имеет меньшее значение (ключ), а узел справа от него имеет большее значение (ключ).
Где в качестве кучи, будучи реализацией двоичного дерева, использует следующее определение:
Если A и B являются узлами, где B является дочерним узлом A, то значение (ключ) A должно быть больше или равно значению (ключу) B. То есть ключ (A) ≥ ключ (B)).
http://wiki.answers.com/Q/Difference_between_binary_search_tree_and_heap_tree
Я задавал тот же вопрос сегодня на экзамене, и я понял его правильно. улыбка...:)
Другое использование BST над Heap; из-за важной разницы:
- Нахождение преемника и предшественника в BST займет O(ч) времени. ( O(logn) в сбалансированном BST)
- находясь в куче, потребуется O(n) время, чтобы найти преемника или предшественника какого-либо элемента.
Использование BST поверх кучи. Теперь допустим, что мы используем структуру данных для хранения времени посадки рейсов. Мы не можем запланировать полет на посадку, если разница во времени посадки меньше, чем "d". И предположим, что многие рейсы запланированы для посадки в структуре данных (BST или Heap).
Теперь мы хотим запланировать еще один рейс, который приземлится в t. Следовательно, нам нужно вычислить разницу t с ее преемником и предшественником (должно быть>d). Таким образом, для этого нам понадобится BST, который делает это быстро, т. Е. В O(logn), если сбалансирован.
Отредактированный:
Сортировка BST занимает O(n) время, чтобы напечатать элементы в отсортированном порядке (обход Inorder), в то время как Heap может сделать это за O(n logn) время. Heap извлекает элемент min и повторно накапливает массив, что заставляет его выполнять сортировку за время O(n logn).
Вставка всех n элементов из массива в BST занимает O(n logn). n элементов в массиве могут быть вставлены в кучу за O(n) раз. Что дает кучу определенное преимущество
Куча — это конкретная структура данных для реализации приоритетной очереди.
Нет причин сохранять наш коэффициент ветвления фиксированным и равным 2. В общем случае у нас могут быть d-ичные деревья:
Деревья, используемые для кучи, являются полными деревьями. Кучи создаются для получения элемента с наивысшим приоритетом в данных. Однако бинарный поиск, как следует из названия, предназначен для поиска.
Кучи не годятся для проверки того, хранится ли в них элемент. У вас нет другого выбора, кроме как пройтись по всем элементам, пока не найдете тот, который ищете, или мы дойдем до конца массива. Это означает алгоритм линейного времени. это
O(log(n))для бинарных деревьев поиска.Однако двоичное дерево поиска не допускает дубликатов, в отличие от кучи.
Двоичное дерево поиска упорядочено, а куча — нет.
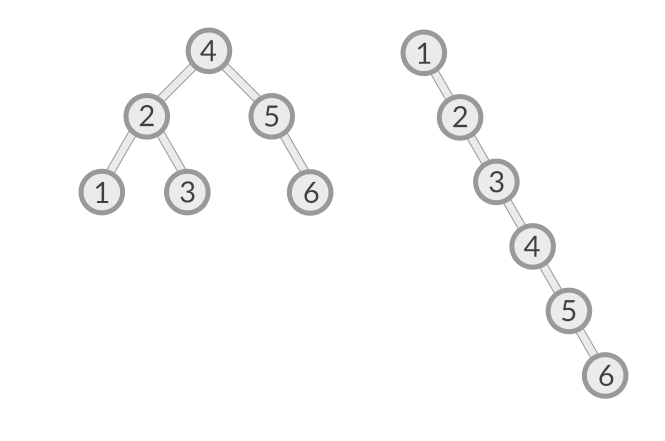
Вставка и удаление займут время O(log(n)) в куче. В двоичном дереве поиска это может занять до O(n) времени, если дерево полностью несбалансировано. На изображении ниже вы видите два BST, правый связан, поэтому вставка и удаление могут занять O(N), но для левого O(Log(N))
Куча может быть построена за линейное время, однако для создания BST требуется O(n * log(n)).
Кучи — это полные деревья. Это очень важный факт. Потому что, когда вы вставляете, вы должны вставлять с последнего, чтобы после замены у вас была полная древовидная структура. Точно так же, когда вы удаляете, удаление начинается с корня, вы удаляете корень, а затем, чтобы сохранить полную древовидную структуру, последний элемент в дереве должен быть вставлен в корень.
Куча просто гарантирует, что элементы на более высоких уровнях больше (для max-heap) или меньше (для min-heap), чем элементы на более низких уровнях
Мне нравится приведенный выше ответ, и я оставляю свой комментарий более конкретным для моих потребностей и использования. Я должен был получить список n местоположений, найти расстояние от каждого местоположения до определенной точки, скажем (0,0), а затем вернуть местоположения, имеющие меньшее расстояние. Я использовал Приоритетную очередь, которая является кучей. Для поиска расстояний и помещения в кучу мне потребовалось n(log(n)) n-положений log (n) каждой вставки. Затем для получения m с наименьшими расстояниями потребовалось m(log(n)) m-положений log (n) удалений накопления.
Если бы мне пришлось делать это с BST, мне потребовалось бы n (n) вставка в худшем случае.(Скажем, первое значение очень меньше, а все остальные идут последовательно все длиннее и длиннее, а дерево охватывает только правого или левого потомка. в случае все меньшего и меньшего. Мин потребовалось бы время O (1), но я снова должен был уравновесить. Таким образом, из моей ситуации и всех приведенных выше ответов я получаю, когда вы только после того, как значения на минимальной или максимальной приоритетной основе идут для кучи.