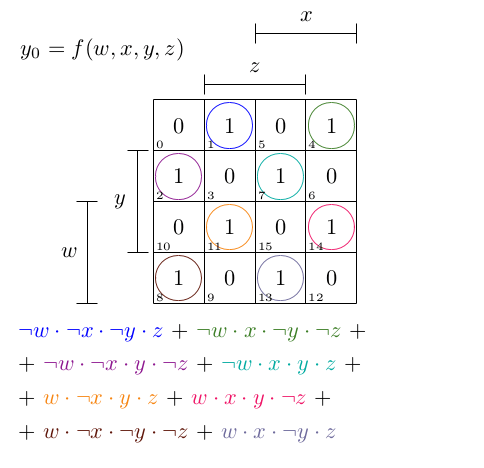Схемы, использующие технику карт Карно

Question

Должна быть разработана комбинационная схема, которая подсчитывает количество появлений 1 бита на 4-битном входе. Однако вход 1111 является недопустимым входом для схемы, и выход в этом случае будет 00.

Один действительный вход для такой схемы может быть 1110 с выходом 11; другой действительный вход может быть 1010 с выходом 10.

Нарисуйте таблицу истинности для схемы. Используйте карту Карно, чтобы спроектировать схему и нарисовать ее, используя И, ИЛИ и НЕ ворота.

Answer 1

Поскольку в 4-битном входе может быть не более 4-х входов, мы можем закодировать выход в 3-битное двоичное число.

Таблица истинности будет выглядеть так:

 w x y z   y_2 y_1 y_0
---------+-------------   number of positive bits
 0 0 0 0 |  0   0   0   ~ 0
 0 0 0 1 |  0   0   1   ~ 1
 0 0 1 0 |  0   0   1   ~ 1
 0 0 1 1 |  0   1   0   ~ 2
---------+-------------
 0 1 0 0 |  0   0   1   ~ 1
 0 1 0 1 |  0   1   0   ~ 2
 0 1 1 0 |  0   1   0   ~ 2
 0 1 1 1 |  0   1   1   ~ 3
---------+-------------
 1 0 0 0 |  0   0   1   ~ 1
 1 0 0 1 |  0   1   0   ~ 2
 1 0 1 0 |  0   1   0   ~ 2
 1 0 1 1 |  0   1   1   ~ 3
---------+------------- 
 1 1 0 0 |  0   1   0   ~ 2
 1 1 0 1 |  0   1   1   ~ 3
 1 1 1 0 |  0   1   1   ~ 3
 1 1 1 1 |  1   0   0   ~ 4

НО! Выход в вашем случае только на два бита. Ваша спецификация также считает ввод 1111 недействительным с выводом 00. поэтому вы можете просто удалить наиболее значимый столбец в таблице истинности, и никаких других изменений не будет:

 w x y z   y_1 y_0
---------+---------   number of positive bits
 0 0 0 0 |  0   0   ~ 0
 0 0 0 1 |  0   1   ~ 1
 0 0 1 0 |  0   1   ~ 1
 0 0 1 1 |  1   0   ~ 2
---------+-------------
 0 1 0 0 |  0   1   ~ 1
 0 1 0 1 |  1   0   ~ 2
 0 1 1 0 |  1   0   ~ 2
 0 1 1 1 |  1   1   ~ 3
---------+-------------
 1 0 0 0 |  0   1   ~ 1
 1 0 0 1 |  1   0   ~ 2
 1 0 1 0 |  1   0   ~ 2
 1 0 1 1 |  1   1   ~ 3
---------+------------- 
 1 1 0 0 |  1   0   ~ 2
 1 1 0 1 |  1   1   ~ 3
 1 1 1 0 |  1   1   ~ 3
 1 1 1 1 |  0   0   ~ invalid, showing zeros

Теперь вы можете использовать разные стили для минимизации выходных функций y_1 а также y_0, но я думаю, что карты Карно подходят для этого.

Перенесите строки таблицы истинности для каждой из выходных функций в отдельную K-карту, используя индексы (номер строки в таблице, проиндексированный с нуля) или сравнивая комбинации переменных.

Для функции вывода y_0 итоговая K-карта выглядит следующим образом, и, как вы можете видеть, это минимизированная функция SOP (DNF; дизъюнкция конъюнкций), в которой не найдено более крупных групп (членов).

y_0 = ¬w·¬x·¬y·z + ¬w·x·¬y·¬z + ¬w·¬x·y·¬z + ¬w·x·y·z 
       + w·¬x·y·z + w·x·y·¬z + w·¬x·¬y·¬z + w·x·¬y·z

Для наиболее значимого бита вывода я выбрал POS (CNF; соединение дизъюнкций), потому что меньше случаев 0 биты чем 1 биты на выходе.

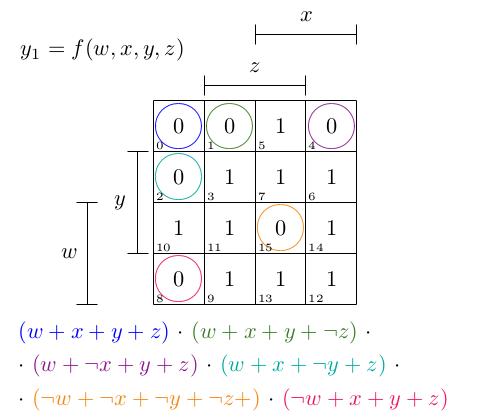
Функция вывода может быть как в y_0 описывается выделением всех правильных битов. В этом случае это будут K-карта и функция:

y_1 = (w + x + y + z) · (w + x + y + ¬z) · (w + ¬x + y + z) 
      · (w + x + ¬y + z) · (¬w + ¬x + ¬y + ¬z) · (¬w + x + y + z)

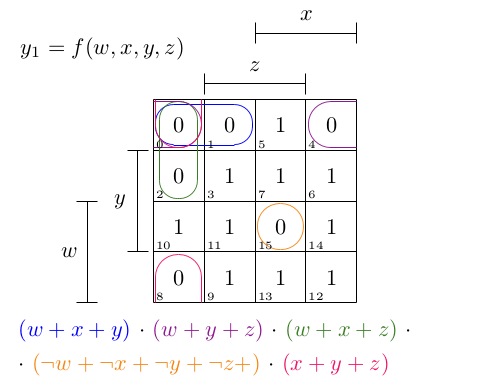
Но это можно свести к минимуму для этой функции вывода в K-карте:

y_1 = (w + x + y) · (w + y + z) · (w + x + z) 
      · (¬w + ¬x + ¬y + ¬z) · (x + y + z) 

После этого вы можете просто использовать правильные ворота или преобразовать их в более подходящую комбинацию ворот, используя сетки Ротта.