Определите граф в Прологе: ребро и путь, определяя, есть ли путь между двумя вершинами

Я очень новичок в Прологе. Я определил в graph.pl следующий график:

график

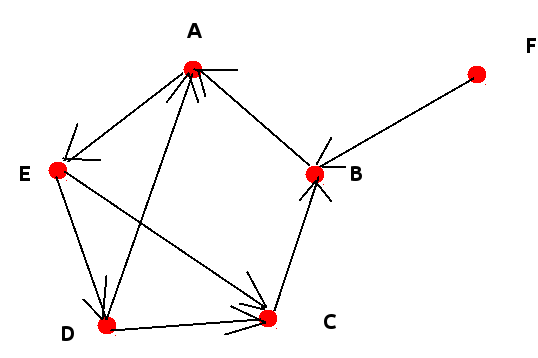
А вот мой код Пролога:

edge(a,e).
edge(e,d).
edge(d,c).
edge(c,b).
edge(b,a).
edge(d,a).
edge(e,c).
edge(f,b).
path(X,X).
path(X,Y):- edge(X,Z) ; path(Z,Y).

Я так понимаю: между вершинами есть путь X и вершина Y только если между вершиной есть ребро X и вершина Z И есть путь между вершинами Z и вершина Y (какая-то рекурсия).

Правильно ли это для представленного графика? Когда я спрашиваю Пролога о пути между вершинами A и вершина F это дает мне true... что даже не правильно! Что может быть не так в этом коде?

Источник

4 ответа

Решение

Циклы на графике. Вам нужно отследить, какие узлы вы посещаете, и проверить их. Попробуйте это, используя вспомогательный предикат с аккумулятором для отслеживания посещенных узлов:

path(A,B) :-   % two nodes are connected, if
  walk(A,B,[]) % - if we can walk from one to the other,
  .            % first seeding the visited list with the empty list

walk(A,B,V) :-       % we can walk from A to B...
  edge(A,X) ,        % - if A is connected to X, and
  not(member(X,V)) , % - we haven't yet visited X, and
  (                  % - either
    B = X            %   - X is the desired destination
  ;                  %   OR
    walk(X,B,[A|V])  %   - we can get to it from X
  )                  %
  .                  % Easy!

edge(a,e).
edge(e,d).
edge(d,c).
edge(c,b).
edge(b,a).
edge(d,a).
edge(e,c).
edge(f,b).
Источник

Если вам интересно узнать, существует ли путь, но не обязательно в фактическом пути, вычислите транзитивное замыкание бинарного отношения edge/2,

К счастью для вас, переходное замыкание - обычная идиома в прологе!

Выразить нерефлексивное транзитивное замыкание edge/2, используйте мета-предикат closure/3 - определено в предыдущем вопросе " Определение рефлексивного транзитивного замыкания ":

? - замыкание (ребро, X, Y).
   X = a, Y = e;  X = a, Y = d;  X = a, Y = c;  ...

Обратите внимание, что closure/3 имеет очень хорошие свойства завершения.

Если все пункты edge/2 являются наземными фактами, closure(edge, _, _) заканчивается универсально! Посмотрите:

?- closure(edge, _, _), false.
false.
Источник

Используемый вами формат (edge ​​/2) имеет смысл для изучения Пролога, и вы должны следовать советам mbratch по поводу учебника.

На самом деле, есть хорошие альтернативы, которые уже доступны, в некоторых случаях с полезными предикатами, готовыми к использованию: например, в библиотеке ( ugraph) есть достижимая/3. Теперь, с вашими данными, этот предикат пути / 2

path(X,Y) :-
    findall(A-B, edge(A,B), Es),
    vertices_edges_to_ugraph([],Es,G),
    reachable(X,G,Path),
    member(Y,Path).

делает

?- path(a,X).
X = a ;
X = b ;
X = c ;
X = d ;
X = e.

Давайте посмотрим, что это значит:

findall(A-B, edge(A,B), Es)

положить в Es все ребра, с обозначениями, как того требует библиотека,

vertices_edges_to_ugraph([],Es,G)

строит в G соответствующий граф

reachable(X,G,Path)

сделать список Путь всех вершин, достижимых (дух) из X

member(Y,Path)

посмотрите, присутствует ли Y в Path.

Так как я запросил Y бесплатно, я получаю все достижимые вершины из X, которые я связал с a,

Источник

Это проверка в цикле! Я выполнил пример с trace. Команда перед рукой, и увидел, что программа возвращается к задаче, чтобы найти путь от a до f после циклического обхода. Для пути (a, f) необходимо, чтобы путь (e, f) был истинным, следуя коротким обозначениям, мы должны быть истинными:

(d, f), (c, f), (b, f), затем снова (a, f).

Для разрешения цикла вам нужен механизм предотвращения цикла. Моей первой идеей было бы сохранить список имен узлов, а также проверить, не содержит ли этот список текущий X при проверке пути.

Источник
Другие вопросы по тегам