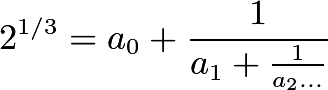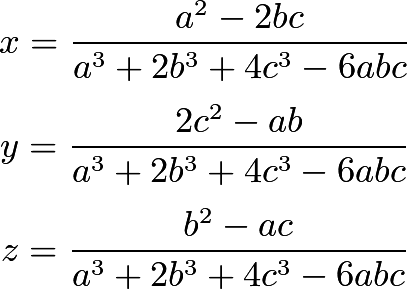Нахождение непрерывной дроби 2^(1/3) с очень высокой точностью

Question

Здесь я буду использовать обозначения

Можно найти непрерывную дробь числа, вычисляя ее, затем применяя определение, но для этого требуется как минимум O(n) битов памяти, чтобы найти₀, a₁... a_n, на практике это значительно хуже. Используя двойную точность с плавающей запятой, можно найти только₀, a₁... a₁₉.

Альтернативой является использование того факта, что если a, b, c являются рациональными числами, то существуют уникальные рациональные числа p, q, r, такие что 1/(a ​​+ b * 2^1/3+ c * 2^2/3) = x + y * 2^1/3+ z * 2^2/3, а именно

Поэтому, если я представляю x,y и z с абсолютной точностью, используя рациональную библиотеку надбавки, я могу получить пол (x + y * 2^1/3+ z * 2^2/3) точно, только с двойной точностью для 2^1/3 и 2^2/3, потому что мне нужно, чтобы оно было в пределах 1/2 от истинного значения. К сожалению, числители и знаменатели x,y и z растут значительно быстрее, и если вместо этого вы используете обычные числа с плавающей точкой, ошибки быстро накапливаются.

Таким образом, я смог вычислить₀,₁...₁₀₀₀₀ за час, но каким-то образом Mathematica может сделать это за 2 секунды. Вот мой код для справки

#include <iostream>

#include <boost/multiprecision/cpp_int.hpp>
namespace mp = boost::multiprecision;

int main()
{
    const double t_1 = 1.259921049894873164767210607278228350570251;
    const double t_2 = 1.587401051968199474751705639272308260391493;
    mp::cpp_rational p = 0;
    mp::cpp_rational q = 1;
    mp::cpp_rational r = 0;
    for(unsigned int i = 1; i != 10001; ++i) {
        double p_f = static_cast<double>(p);
        double q_f = static_cast<double>(q);
        double r_f = static_cast<double>(r);
        uint64_t floor = p_f + t_1 * q_f + t_2 * r_f;
        std::cout << floor << ", ";
        p -= floor;
        //std::cout << floor << " " << p << " " << q << " " << r << std::endl;
        mp::cpp_rational den = (p * p * p + 2 * q * q * q +
                                4 * r * r * r - 6 * p * q * r);
        mp::cpp_rational a = (p * p - 2 * q * r) / den;
        mp::cpp_rational b = (2 * r * r - p * q) / den;
        mp::cpp_rational c = (q * q - p * r)     / den;
        p = a;
        q = b;
        r = c;
    }
    return 0;
}

Answer 1

Алгоритм Лагранжа

Алгоритм описан, например, в книге Кнута "Искусство компьютерного программирования", том 2 (пример 13 в разделе 4.5.3 "Анализ алгоритма Евклида", стр. 375 в 3-м издании).

Позволять f быть полиномом от целочисленных коэффициентов, у которых единственный действительный корень является иррациональным числом x0 > 1, Затем алгоритм Лагранжа вычисляет последовательные коэффициенты непрерывной дроби x0,

Я реализовал это в Python

def cf(a, N=10):
    """
    a : list - coefficients of the polynomial,
        i.e. f(x) = a[0] + a[1]*x + ... + a[n]*x^n
    N : number of quotients to output
    """
    # Degree of the polynomial
    n = len(a) - 1

    # List of consecutive quotients
    ans = []

    def shift_poly():
        """
        Replaces plynomial f(x) with f(x+1) (shifts its graph to the left).
        """
        for k in range(n):
            for j in range(n - 1, k - 1, -1):
                a[j] += a[j+1]

    for _ in range(N):
        quotient = 1
        shift_poly()

        # While the root is >1 shift it left
        while sum(a) < 0:
            quotient += 1
            shift_poly()
        # Otherwise, we have the next quotient
        ans.append(quotient)

        # Replace polynomial f(x) with -x^n * f(1/x)
        a.reverse()
        a = [-x for x in a]

    return ans

На моем компьютере требуется около 1 с cf([-2, 0, 0, 1], 10000), (Коэффициенты соответствуют полиному x^3 - 2 чей единственный настоящий корень - 2^(1/3). Выходные данные совпадают с полученными от Wolfram Alpha.

Предостережение

Коэффициенты полиномов, вычисленные внутри функции, быстро становятся довольно большими целыми числами. Таким образом, этот подход требует некоторой реализации bigint на других языках (Pure python3 имеет дело с этим, но, например, numpy - нет).

Answer 2

Возможно, вам больше повезет, если вы вычислите 2^(1/3) с высокой точностью, а затем попытаетесь извлечь из этого непрерывную дробь, используя интервальную арифметику, чтобы определить, достаточна ли точность.

Вот мой пример в Python, использующий итерацию Галлея для вычисления 2^(1/3) в фиксированной точке. Мертвый код - это попытка вычислить взаимные вычисления с фиксированной точкой более эффективно, чем Python, с помощью итерации Ньютона - без кубиков.

Время от моей машины составляет около тридцати секунд, в основном потраченных на извлечение непрерывной дроби из представления с фиксированной точкой.

prec = 40000
a = 1 << (3 * prec + 1)
two_a = a << 1
x = 5 << (prec - 2)
while True:
    x_cubed = x * x * x
    two_x_cubed = x_cubed << 1
    x_prime = x * (x_cubed + two_a) // (two_x_cubed + a)
    if -1 <= x_prime - x <= 1: break
    x = x_prime

cf = []
four_to_the_prec = 1 << (2 * prec)
for i in range(10000):
    q = x >> prec
    r = x - (q << prec)
    cf.append(q)
    if True:
        x = four_to_the_prec // r
    else:
        x = 1 << (2 * prec - r.bit_length())
        while True:
            delta_x = (x * ((four_to_the_prec - r * x) >> prec)) >> prec
            if not delta_x: break
            x += delta_x
print(cf)