Реализация Deque с использованием 3 стеков (амортизированное время O(1))

Question

У меня есть этот вопрос для howmework:

Реализуйте Deque, используя 3 стека. У Deque есть такие операции: InsertHead, InsertTail, DeleteHead,DeleteTail. Докажите, что амортизированное время для каждой операции равно O(1).

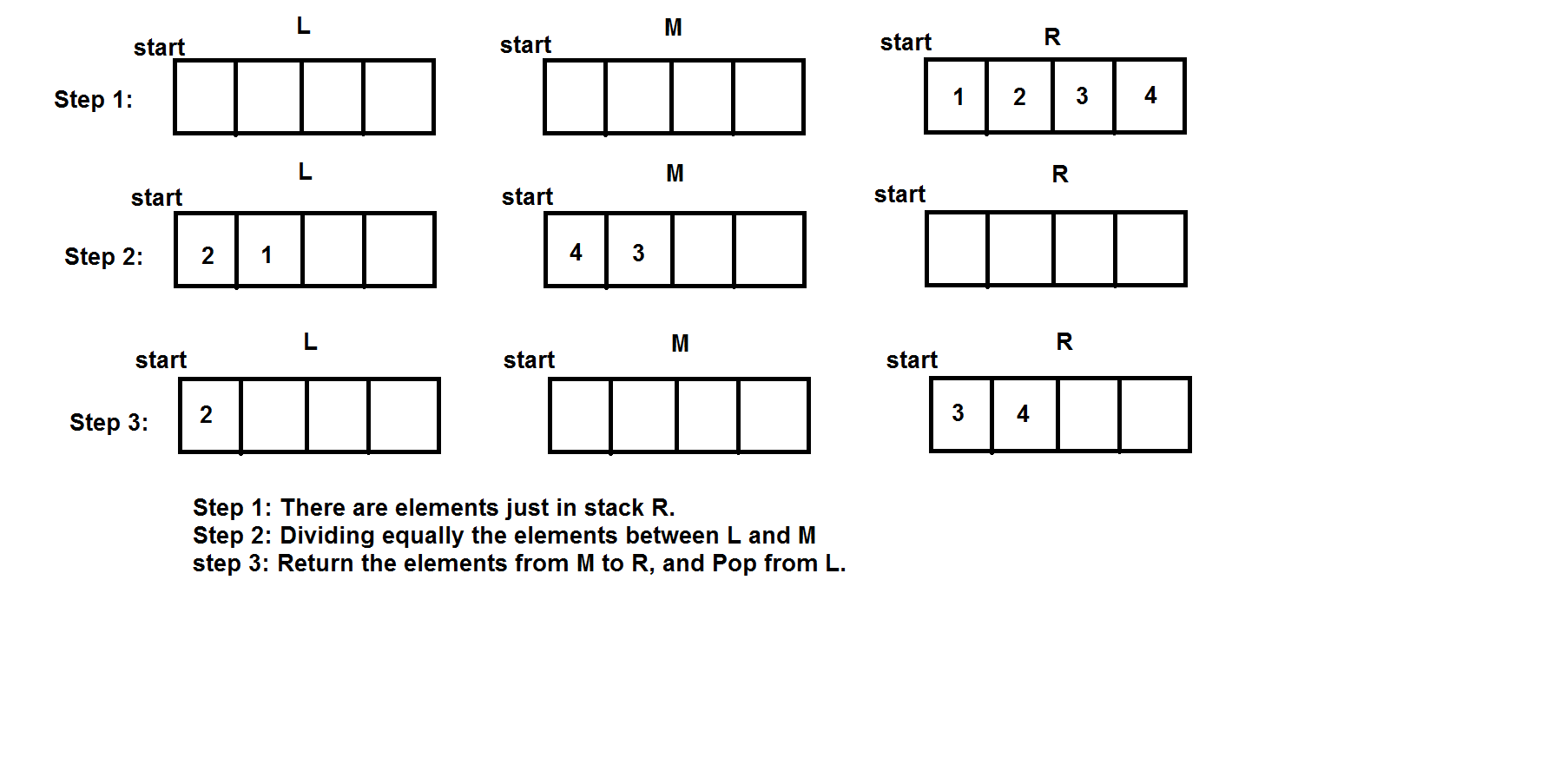
То, что я пытался, это посмотреть на проблему как на проблему Ханоя. Итак, давайте назовем стеки: L(слева), M (в середине), R(справа).

Реализации псевдокода:

InsertHead(e):
     L.push(e);

DeleteHead(e):
     L is empty:

       while R is not empty:
          pop and insert the element to M;
       pop M;
       while M is not empty:
         pop and insert the element to R;

     L is not empty:    
       L.pop(e);

InsertTail и DeleteTail работают по тому же принципу, что и описанные выше реализации. Как я могу доказать, что амортизированное время равно O (1)? потому что в L может быть N элементов, и цикл wile примет O (n), теперь, если я вызову deleteHead N раз, чтобы вычислить амортизированное время, сложность не будет O(n^2)?

Может ли кто-нибудь помочь мне, как я могу доказать, что вышеуказанные реализации принимают O (1) в амортизированное время?

Answer 1

Мы продолжаем использовать потенциальный метод; определить

Phi = C |L.size - R.size|

Для некоторой постоянной Cдля которого мы выберем значение позже. ПозволятьPhi_t обозначим потенциал после tоперации. Обратите внимание, что в "сбалансированном" состоянии, когда оба стека имеют равный размер, структура данных имеет потенциал 0.

Потенциал в любой момент времени - это постоянная разница в количестве элементов в каждой стопке. Обратите внимание, чтоPhi_0 = 0 поэтому потенциал равен нулю при инициализации структуры.

Ясно, что операция проталкивания увеличивает потенциал не более чем на C. Операция pop, которая не пропускает (т.е. когда соответствующий стек непуст), также изменяет потенциал не более чем наC. Обе эти операции имеют истинную стоимость 1, следовательно, они имеют амортизированную стоимость.1 + C.

Когда происходит операция выталкивания и вызывает промах (когда стек, из которого мы хотим вытолкнуть, пуст), истинная стоимость операции составляет1 + 3/2 * R.size когда мы пытаемся выскочить из L, и наоборот, когда мы выходим из R. Это потому, что мы перемещаем половину элементов R в M и обратно, а другую половину элементов R в L.+1 необходим из-за финального треска от L после выполнения этой операции перебалансировки.

Следовательно, если мы возьмем C := 3/2, то операция pop при возникновении промаха имеет амортизированную стоимость 1, потому что потенциал уменьшается с3/2 * R.size до 0 из-за ребалансировки, и тогда мы можем понести дополнительные расходы в размере 3/2 от попа, который возникает после ребалансировки.

Другими словами, каждая операция имеет амортизированную стоимость, ограниченную константой.

Наконец, поскольку начальный потенциал равен 0, а потенциал всегда неотрицателен, каждая операция имеет амортизированную стоимость O(1), как требуется.