Нахождение Количество способов

Question

Для заданных M цифр от 1 до 9 найдите количество способов сформировать число из N цифр, повторив одну или несколько заданных цифр таким образом, чтобы каждая из M цифр присутствовала в числе из N цифр хотя бы один раз. Пример, если М = 3 и N = 4 Ответ 36.

Пояснение - пусть три цифры равны 1 2 3, наше N = 4, число может быть 1123, 3211, 1132,..... повторяя 1, аналогично повторяя 2 и три, мы получим общее число ответов.

Поскольку ответ большой, найдите ответ% 10000000007. 1 ≤ M ≤ N ≤ 100.

Answer 1

Поскольку вы не указали, какой язык программирования использовать, я буду использовать любой язык, который я предпочитаю (например, Java). Если вы предпочитаете другой язык программирования, вы можете пометить мой код как псевдокод (я добавил достаточно много комментариев в коде, чтобы объяснить, что происходит) и перевести на другой язык программирования самостоятельно.

осветление

Прежде чем приступить к решению проблемы, я хотел бы отметить, что входные аргументы должны представлять собой набор цифр S и целое число N, которое по крайней мере имеет размер S. То, как вы формулируете проблему, предполагает, что входными аргументами являются M и N. Это вводит в заблуждение, потому что, если вы считаете, S = {1, 1, 3} а также N = 4, тогда очевидно, что количество комбинаций в этом случае меньше, чем в вашем примере.

Идея высокого уровня

Основным методом решения этой проблемы является (не удивительно) динамическое программирование, подзадачи P(L, T) индексируются двумя параметрами: (1) длина L числа, которое будет построено; и (2) набор цифр T это должно появиться при построении L-значного числа. В вашем примере параметры: (1) L = 4; и (2) T = {1, 2, 3},

Предположим, теперь мы хотим решить проблему P(L, S), Давайте выберем произвольную цифру a из цифр алфавита (т.е. все цифры от 1 до 9, которые появляются во входном аргументе S).

• Если a в S, то количество L-цифр, начинающихся с a дан кем-то P(L - 1, S \ {a}),

• С другой стороны, если a не в S, то количество L-цифр, начинающихся с a дан кем-то P(L - 1, S),

Поэтому мы имеем следующую формулу:

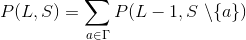
Здесь Г обозначает цифру алфавита, а S \ {a} = S если a не в S,

И базовые случаи для этой проблемы P(0, Ø) = 1 (Ø обозначает пустой набор), и P(L, S) = 0 если L < |S|,

Код

Обновление: я откатил свой код, чтобы изменить счет 10000000007 (модуль, который вы использовали в своем вопросе) вместо 1000000007 (1 ноль меньше).

Код, написанный на Java, приведен ниже:

import java.util.ArrayList;
import java.util.Collections;
import java.util.HashMap;
import java.util.HashSet;
import java.util.List;
import java.util.Map;
import java.util.Set;


public class Combination {

    /* Input arguments */
    private static int[] inputNums = {1, 2, 3};
    private static final int N = 4;

    // This contains all the valid digits for constructing our N-digit number 
    private static Set<Integer> validDigits;

    // Lookup table for sub-problems to save computation time
    private static Map<String, Long> subProbLookup;

    public static void main(String[] args) {

        validDigits = new HashSet<Integer>();
        List<Integer> initNums = new ArrayList<Integer>();
        subProbLookup = new HashMap<String, Long>();

        // Initiation
        for (int i = 0; i < inputNums.length; i++) {
            validDigits.add(inputNums[i]);
            initNums.add(inputNums[i]);
        }

        // For ensuring the keys for the lookup table are consists
        Collections.sort(initNums);

        System.out.println("The number of combinations is " + countDP(N, initNums));

    }

    private static long countDP(int length, List<Integer> requiredNums) {

        // This corresponds to the case that not all given digits are used
        if (requiredNums.size() > length) {
            return 0;
        }

        // Base Case
        if (requiredNums.size() == 0 && length == 0) {
            return 1;
        }

        // Check for cached result
        final String key = requiredNums.toString() + ";" + length;

        if (subProbLookup.containsKey(key)) {
            return subProbLookup.get(key);
        }

        long count = 0;

        for (Integer i : validDigits) {
            // Generate next sub-problem
            List<Integer> updatedNums = new ArrayList<Integer>(requiredNums);
            if (requiredNums.contains(i)) {
                updatedNums.remove(i);
            }
            count = (count + countDP(length - 1, updatedNums)) % 10000000007L;
        }

        // Cache the result
        subProbLookup.put(key, count);
        return count;
    }

}