Предотвратить nls-fit от падения ниже нуля
Я пытаюсь поместить функцию в R, и поэтому я использую nls(). Есть ли способ предотвратить падение встроенной функции ниже нуля?
Легким обходным путем было бы повысить параметр b0 в целевой функции после подгонки, но на самом деле это не то, чего я хочу, потому что я ожидаю, что реальная подгонка с ограничением положительного результата приведет к лучшему результату.
y=c(m1,m2,m3,m4,m5,m6,m7,m8,m9,m10)
d=data.frame(seq(1, 10, 1),y=y)
fitFun <- function(x, add, b0, b1) {b0 + (x+add)^b1}
m=nls(y~fitFun(x,add,intercept,power),d,start=list(intercept=1,power=3.5,add=2),trace=T)
3 ответа
Большое спасибо за ответы. Возможно, я не дал достаточно информации о своей проблеме, но мне пока не разрешают публиковать фотографии и описывать все, что привело бы к короткому рассказу.
@Roland был совершенно прав: задача оптимизаторов не заботиться о поведении целевой функции, но, как я уже говорил, я предполагаю, что модель исправлена.
Предложение @Ben Bolker ограничить аддитивную часть функции положительными значениями привело к неудовлетворительному результату.
Что я не упомянул, так это то, что от m1 до m10 являются средними значениями сбора данных, которые я записал. Я решил свою проблему, используя дисперсию записанных рядов в качестве весов во время процесса подбора.
y=c(m1,m2,m3,m4,m5,m6,m7,m8,m9,m10)
d=data.frame(seq(1, 10, 1),y=y)
vars = c(var(lt1$V1),var(lt2$V1),var(lt3$V1),var(lt4$V1),var(lt5$V1),var(lt6$V1),var(lt7$V1),var(lt8$V1),var(lt9$V1),var(lt10$V1))
weights = rep(max(vars),10)/vars
fitFun <- function(x, add, b0, b1) {b0 + (x+add)^b1}
m=nls(y~fitFun(x,add,intercept,power),d,weights=weights,start=list(intercept=1,power=3.5,add=2),trace=T)
Вы ищете это? Ограничить параметры, чтобы сделать прогноз неотрицательным, может быть непросто, если прогноз является труднообращаемой функцией параметров, но в этом случае нам просто нужно потребовать b0>=0... используя пример @Roland,
fit2 <- nls(y~b0+(x+add)^b1,
algorithm="port",
lower=c(b0=0,b1=-Inf,add=-Inf),
data=df,start=list(b0=1,b1=3.5,add=2))
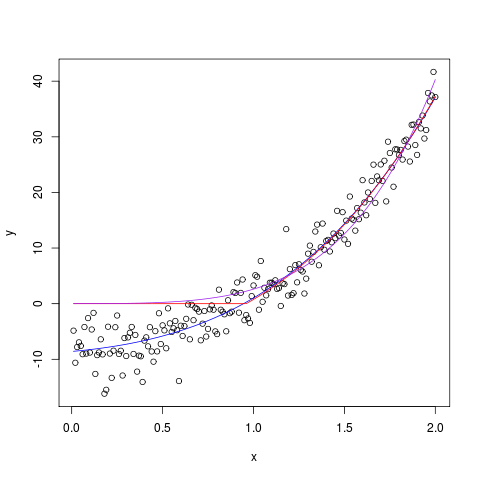
lines(predict(fit2)~df$x,col="purple")
В последующем синий цвет - это оригинальная непринужденная посадка; красный подходит @ Роланду; и фиолетовый - подгонка выше.
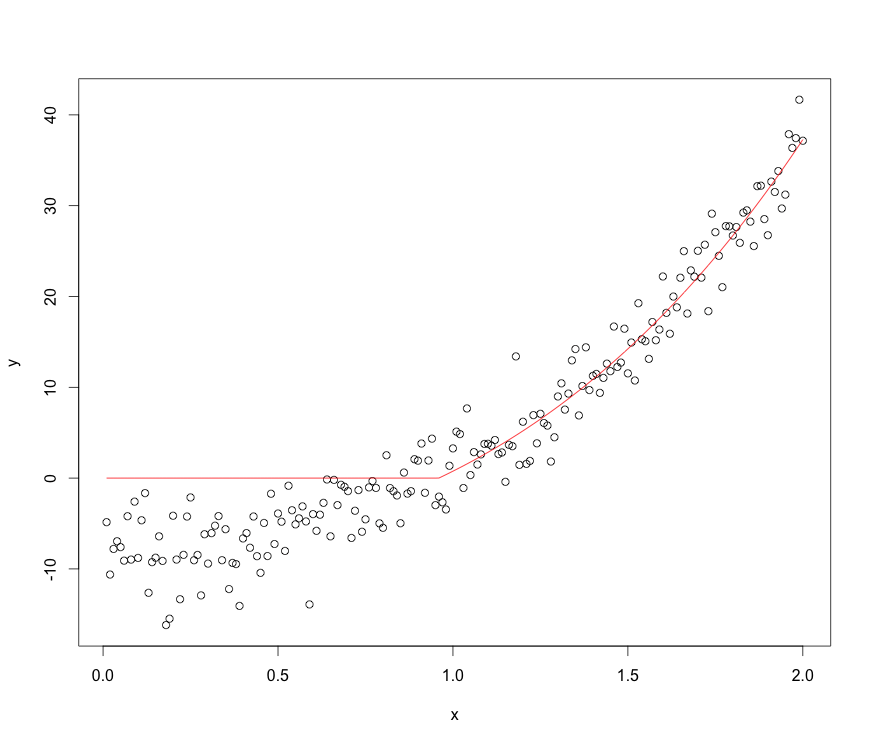
Вы должны изменить свою модель. Для этого вам нужно определить, что должно произойти, если значения функции упадут ниже нуля. Вот пример, который устанавливает эти значения в 0.
x <- 1:200/100
set.seed(42)
y <- -10+(x+1)^3.5+rnorm(length(x),sd=3)
df <- data.frame(x,y)
plot(y~x,data=df)
fitFun <- function(x, add, b0, b1) {
res <- b0 + (x+add)^b1
res[res<0] <- 0
res
}
fit <- nls(y~fitFun(x,add,intercept,power),
data=df,start=list(intercept=1,power=3.5,add=2))
summary(fit)
lines(predict(fit)~df$x,col="red")