Получение не-одиночных кластерных идентификаторов в скучной иерархической кластеризации

Question

Согласно документации Scipy, мы можем получить идентификаторы кластеров для не-одноэлементных кластеров. Я задавал один и тот же вопрос о переполнении стека один раз. Но, похоже, это не лучшее решение, и я попробовал несколько. Тем не менее я не мог получить кластерные идентификаторы для не-синглетонов.

import numpy as np
import scipy.cluster.hierarchy
import matplotlib.pyplot as plt
from scipy.cluster.hierarchy import dendrogram, linkage

mat = np.array([[ 0. , 1. , 3.  ,0. ,2.  ,3.  ,1.],
 [ 1. , 0. , 3. , 1.,  1. , 2. , 2.],
 [ 3.,  3. , 0.,  3. , 3.,  3. , 4.],
 [ 0. , 1. , 3.,  0. , 2. , 3.,  1.],
 [ 2. , 1.,  3. , 2.,  0. , 1.,  3.],
 [ 3. , 2.,  3. , 3. , 1. , 0. , 3.],
 [ 0. , 2.,  4. , 1. , 3.,  3. , 0.],
 [ 1. , 2.,  5. , 1. , 3.,  1. , 0.],
 [ 4. , 2.,  4. , 1. , 3.,  0. , 0.],
 [ 1. , 2.,  2. , 1. , 0.,  3. , 0.]])

n = len(mat)


linkage_matrix = linkage(mat, "complete")



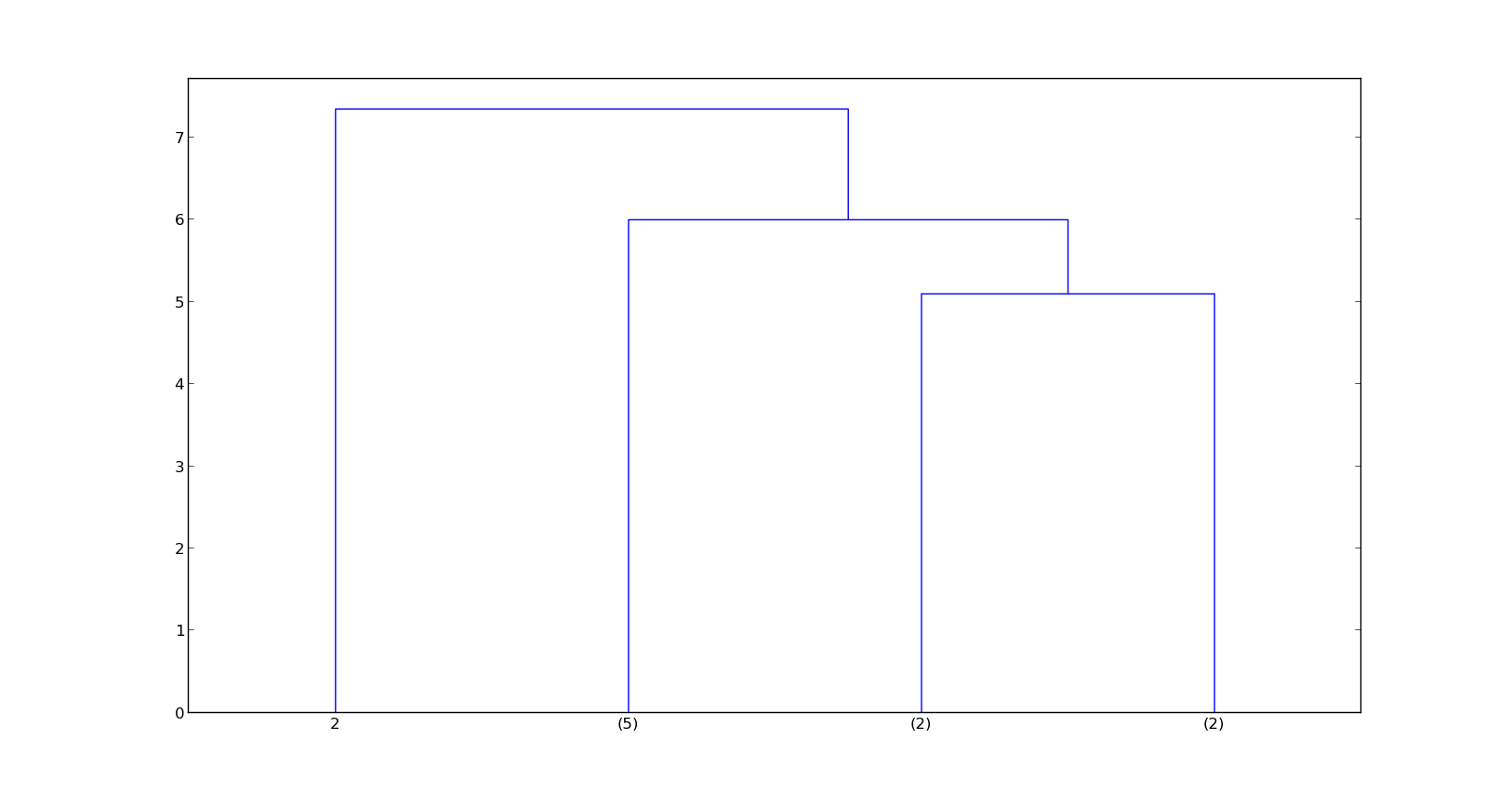
D = dendrogram(linkage_matrix,
              p=4,
              color_threshold=1,
              truncate_mode='lastp',
              distance_sort='ascending')

plt.show()

Просто как узнать, кто внутри (5),(2) и (2)? Это очень простая диаграмма, но она становится более сложной со множеством не-одиночных кластеров.