Matlab - Сбой функции обнаружения коллизий между отрезками и окружностью

Question

Matlab - Сбой функции обнаружения коллизий между отрезками и окружностью

Уже существует много вопросов, касающихся того, как обнаружить столкновения между отрезком и окружностью.

В моем коде я использую Matlab's linecirc затем сравнивает точки пересечения, которые он возвращает, с концами моих отрезков, чтобы убедиться, что точки находятся внутри линии (linecirc предполагает бесконечную линию, которую я не хочу / не хочу).

Копирование и добавление некоторых sprintf звонки в linecirc Функция показывает, что она рассчитывает точки, как и предполагалось. Похоже, они теряются моей функцией.

Мой код ниже:

function cutCount = getCutCountHex(R_g, centre)
clf;
cutCount = 0;

% Generate a hex grid
Dg = R_g*2;
L_b = 62;

range = L_b*8;

dx = Dg*cosd(30);
dy = 3*R_g;
xMax = ceil(range/dx); yMax = ceil(range/dy);
d1 = @(xc, yc) [dx*xc dy*yc];
d2 = @(xc, yc) [dx*(xc+0.5) dy*(yc+0.5)];

centres = zeros((xMax*yMax),2);
count = 1;

for yc = 0:yMax-1
    for xc = 0:xMax-1
        centres(count,:) = d1(xc, yc);
        count = count + 1;
        centres(count, :) = d2(xc, yc);
        count = count + 1;
    end
end

for i=1:size(centres,1)
    centres(i,:) = centres(i,:) - [xMax/2 * dx, yMax/2 * dy];
end

hold on
axis equal

% Get counter for intersected lines
[VertexX, VertexY] = voronoi(centres(:,1), centres(:,2));
numLines = size(VertexX, 2);
for lc = 1:numLines
    segStartPt = [VertexX(1,lc) VertexY(1,lc)];
    segEndPt = [VertexX(2,lc) VertexY(2,lc)];
    slope = (segEndPt(2) - segStartPt(2))/(segEndPt(1) - segStartPt(1));
    intercept = segEndPt(2) - (slope*segEndPt(1));
    testSlope = isinf(slope);
    if (testSlope(1)==1)
        % Pass the x-axis intercept instead
        intercept = segStartPt(1);
    end
    [xInterceptionPoints, yInterceptionPoints] = ...
        linecirc(slope, intercept, centre(1), centre(2), L_b);

    testArr = isnan(xInterceptionPoints);
    if (testArr(1) == 0) % Line intersects. Line segment may not.
        interceptionPoint1 = [xInterceptionPoints(1), yInterceptionPoints(1)];
        interceptionPoint2 = [xInterceptionPoints(2), yInterceptionPoints(2)];

        % Test if first intersection is on the line segment
        p1OnSeg = onSeg(segStartPt, segEndPt, interceptionPoint1);
        p2OnSeg = onSeg(segStartPt, segEndPt, interceptionPoint2);
        if (p1OnSeg == 1)
            cutCount = cutCount + 1;
            scatter(interceptionPoint1(1), interceptionPoint1(2), 60, 'MarkerFaceColor', 'r', 'MarkerEdgeColor', 'k');
        end

        % Test if second intersection point is on the line segment
        if (interceptionPoint1(1) ~= interceptionPoint2(1) || interceptionPoint1(2) ~= interceptionPoint2(2)) % Don't double count touching points
            if (p2OnSeg == 1)
                cutCount = cutCount + 1;
                scatter(interceptionPoint2(1), interceptionPoint2(2), 60, 'MarkerFaceColor', 'r', 'MarkerEdgeColor', 'k');
            end
        end
    end
end

% Plot circle

viscircles(centre, L_b, 'EdgeColor', 'b');
H = voronoi(centres(:,1), centres(:,2));
for i = 1:size(H)
    set(H(i), 'Color', 'g');
end
end

function boolVal = onSeg(segStart, segEnd, testPoint)
bvX = isBetweenOrEq(segStart(1), segEnd(1), testPoint(1));
bvY = isBetweenOrEq(segStart(2), segEnd(2), testPoint(2));
if (bvX == 1 && bvY == 1)
    boolVal = 1;
else
    boolVal = 0;
end
end

function boolVal = isBetweenOrEq(end1, end2, test)
    if ((test <= end1 && test >= end2) || (test >= end1 && test <= end2))
        boolVal = 1;
    else
        boolVal = 0;
    end
end

Он создает гексагональную сетку, а затем вычисляет количество пересечений между кругом, нарисованным с фиксированным радиусом (в данном случае 62), и указанным центром.

scatter звонки показывают места, которые считает функция. Внедрение sprintf звонки в пределах if(p1OnSeg == 1) блок указывает, что моя функция выбрала фиктивные точки пересечения (хотя тогда она правильно с ними работает)

if (interceptionPoint1(1) > -26 && interceptionPoint1(1) < -25)
                sprintf('p1 = [%f, %f]. Vx = [%f, %f], Vy = [%f, %f].\nxint = [%f, %f], yint = [%f, %f]',...
                    interceptionPoint1(1), interceptionPoint1(2), VertexX(1,lc), VertexX(2,lc), VertexY(1,lc), VertexY(2,lc),...
                    xInterceptionPoints(1), xInterceptionPoints(2), yInterceptionPoints(1), yInterceptionPoints(2))
            end

Выходы

p1 = [-25.980762, 0.000000]. Vx = [-25.980762, -25.980762], Vy = [-15.000000, 15.000000].
xint = [-25.980762, -25.980762], yint = [0.000000, 0.000000]

Картина показывает странные точки.

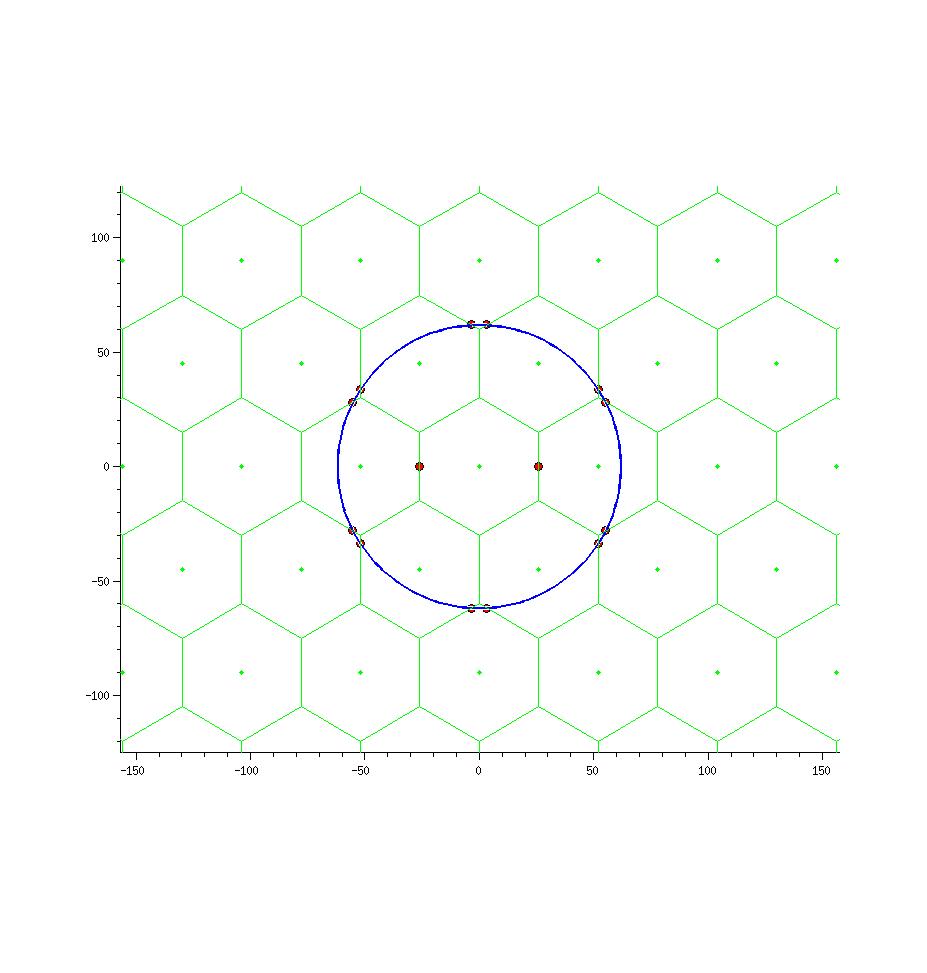
Извините за очень длинный вопрос, но - почему они обнаруживаются. Они не лежат на круге (отображение значений в mylinecirc Функция обнаруживает пересечения около (-25, 55) и (-25, -55) или около того (как и следовало ожидать бесконечной линии).

Перемещение по кругу может удалить эти точки, но иногда это приводит к другим проблемам с обнаружением. В чем дело?

Изменить: Поворот моей сетки, созданной [Vx, Vy] = voronoi(...) и затем удаление точек с очень большими значениями (т. е. близкими к бесконечности и т. д.), по-видимому, решило эту проблему. Удаление "больших" точек значений представляется необходимым, чтобы избежать появления значений NaN в "уклоне" и "пересечении". Я предполагаю, что это связано с возможным небольшим наклоном из-за поворота в сочетании с переполнением ожидаемого перехвата.

Пример кода добавлен ниже. Я также редактировал код Яна де Жира, но это не имело значения для проблемы и поэтому не изменилось в коде вопроса.

%Rotate slightly
RotAngle = 8;
RotMat = [cosd(RotAngle), -sind(RotAngle); sind(RotAngle), cosd(RotAngle)];

for i=1:size(centres,1)
    centres(i,:) = centres(i,:) - [floor(xMax/2) * dx, floor(yMax/2) * dy]; %Translation
    centres(i,:) = ( RotMat * centres(i,:)' ); %Rotation
end


% Get counter for intersected lines
[VertexX, VertexY] = voronoi(centres(:,1), centres(:,2));

% Filter vertices
numLines = size(VertexX, 2);
newVx = [];
newVy = [];
for lc = 1:numLines
    testVec = [VertexX(:,lc) VertexY(:,lc)];
    if ~any(abs(testVec) > range*1.5)
        newVx = [newVx; VertexX(:,lc)'];
        newVy = [newVy; VertexY(:,lc)'];
    end
end
VertexX = newVx';
VertexY = newVy';
numLines = size(VertexX, 2);

Все еще ценю ответы или предложения, чтобы выяснить, почему это происходит. Пример значения, которые вызывают это getCutCountHex(30, [0,0]) а также ...(35, [0,0])

4

matlab line circle line-segment

Источник

user3098505 26 сен '14 в 09:43

1 ответ

Другие вопросы по тегам matlab line circle line-segment

user4086755 28 сен '14 в 13:54 2014-09-28 13:54 · Answer 1 · 2014-09-28 13:54

Я не могу воспроизвести вашу проблему, но я заметил, что ваша функция onSeg() может быть неправильной: она возвращает значение true, если контрольная точка находится в прямоугольнике, а две из четырех угловых точек - это segStart и segEnd.

Функция, которая возвращает истину, если точка находится (или точнее: достаточно близко) к сегменту линии (segStart, segEnd):

function boolVal = onSeg(segStart, segEnd, testPoint)

    tolerance = .5;

    AB = sqrt((segEnd(1)-segStart(1))*(segEnd(1)-segStart(1))+(segEnd(2)-segStart(2))*(segEnd(2)-segStart(2)));
    AP = sqrt((testPoint(1)-segEnd(1))*(testPoint(1)-segEnd(1))+(testPoint(2)-segEnd(2))*(testPoint(2)-segEnd(2)));
    PB = sqrt((segStart(1)-testPoint(1))*(segStart(1)-testPoint(1))+(segStart(2)-testPoint(2))*(segStart(2)-testPoint(2)));

    boolVal = abs(AB - (AP + PB)) < tolerance;

end

подход, который я нашел в одном из ответов здесь: Найти, если точка лежит на отрезке. Я надеюсь, что это решит вашу проблему.