Может ли программа решить, останавливается ли произвольная программа для некоторого ввода?
Существует ли программа (may-halt? P), которая может определить, существует ли вход, чтобы (p input) останавливался?
Я попробовал простую диагонализацию, но она только говорит мне, что (may-halt? Diag-may-halt) должно быть правдой. Это не помогает доказать, существует программа или нет.
Существует ли такая программа?
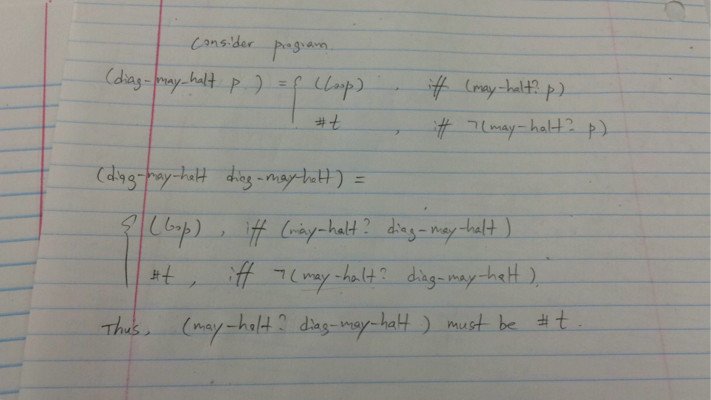
1 ответ
Нету, may-halt? не существует
(Я не думаю, что прямое доказательство диагонализацией было бы менее сложным, чем доказательство того, что проблема Остановки неразрешима; в противном случае это был бы стандартный пример. Вместо этого давайте сведем вашу проблему к проблеме Остановки:)
Предположим, что была программа may-halt? pчто решит программа p останавливается для некоторого ввода. Затем определите:
halt? p x := may-halt? (\y -> if y==x then p x else ⊥)
где вещь в фигурных скобках - производная программа. Давайте разберемся с этим:
halt? p x := may-halt? p'
где p' это программа, которая (я) на входе x вычисляет p x, (ii) на любом другом входе просто зацикливается без завершения:
p' y := if y==x then p x else ⊥
затем may-halt? p' выводит истину тогда и только тогда, когда p x завершается.
Таким образом, для любой программы p и ввод x, halt? p x решил бы, если p x завершается. Но мы знаем, что это невозможно, поэтому may-halt? не существует