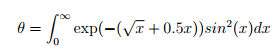Интеграция Монте-Карло с использованием выборки по важности с учетом функции предложения

Question

Учитывая предложение о распространении Laplace:

g(x) = 1/2*e^(-|x|)

и размер выборки n = 1000, Я хочу провести интеграцию Монте-Карло (MC) для оценки θ:

через выборку важности. В конце концов я хочу вычислить среднее и стандартное отклонение этой оценки MC в R, как только я доберусь туда.

---

Изменить (прибыл поздно после ответа ниже)

Это то, что у меня есть для моего кода R:

library(VGAM)
n = 1000
x = rexp(n,0.5)
hx = mean(2*exp(-sqrt(x))*(sin(x))^2)
gx = rlaplace(n, location = 0, scale = 1)

Answer 1

Теперь мы можем написать простую функцию R для выборки из распределения Лапласа:

## `n` is sample size
rlaplace <- function (n) {
  u <- runif(n, 0, 1)
  ifelse(u < 0.5, log(2 * u), -log(2* (1 - u)))
  }

Также напишите функцию для плотности распределения Лапласа:

g <- function (x) ifelse(x < 0, 0.5 * exp(x), 0.5 * exp(-x))

Теперь ваш интеграл:

f <- function (x) {
  ifelse(x > 0, exp(-sqrt(x) - 0.5 * x) * sin(x) ^ 2, 0)
  }

Теперь оценим интеграл по 1000 выборок (set.seed для воспроизводимости):

set.seed(0)
x <- rlaplace(1000)
mean(f(x) / g(x))
# [1] 0.2648853

Также сравните с числовым интегрированием с использованием квадратуры:

integrate(f, lower = 0, upper = Inf)
# 0.2617744 with absolute error < 1.6e-05