В чем разница между двоичными кучами и биномиальными кучами?

Question

Мне нужно знать основное различие между двоичными и биномиальными кучами независимо от их структурного различия, заключающееся в том, что двоичные кучи могут иметь только два дочерних элемента (представление дерева), а биномиальные кучи могут иметь любое количество дочерних элементов.

Мне просто интересно, что такого особенного в организации биномиальной древовидной структуры таким образом, что у первого потомка на одном узле у второго есть у двух третьих есть четыре и так далее?

Что если, если мы используем какое-то нормальное дерево для куч без ограничения двух дочерних элементов, а затем применяем процедуру объединения и просто делаем одну кучу левым дочерним элементом других куч?

Answer 1

Ключевое различие между двоичной кучей и биномиальной кучей состоит в том, как структурированы кучи. В двоичной куче куча представляет собой одно дерево, которое представляет собой полное двоичное дерево. В биномиальной куче, куча представляет собой набор меньших деревьев (то есть лес деревьев), каждое из которых является биномиальным деревом. Полное двоичное дерево может быть построено так, чтобы содержать любое количество элементов, но количество элементов в биномиальном дереве некоторого порядка n всегда равно 2ⁿ. Следовательно, нам нужно только одно полное двоичное дерево для резервного копирования двоичной кучи, но нам может потребоваться несколько биномиальных деревьев для резервного копирования биномиальной кучи. Интересно, что порядки биномиальных деревьев, используемых в биномиальной куче, соответствуют 1 битам, установленным в двоичном представлении числа элементов в лесу.

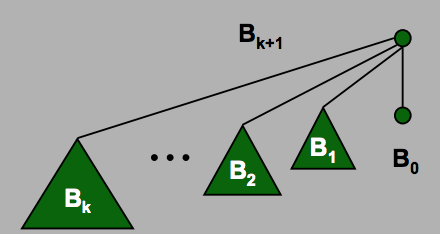
Причиной организации биномиальных куч, как они есть, является то, что биномиальное дерево порядка n всегда имеет ровно 2ⁿ узлов. Это позволяет нам делать предположения о количестве элементов в биномиальном дереве без фактической проверки структуры этого дерева. С другой стороны, полное двоичное дерево некоторой высоты h может иметь переменное число узлов в нем в зависимости от того, как заполнена последняя строка. Тот факт, что каждый из дочерних элементов должен иметь очень точно определенную структуру, также может быть использован для доказательства того, что число дочерних элементов не превышает O(log n), где n - общее количество узлов в куче, что означает, что стоимость удаления мин не слишком велика.

Важной деталью этого является то, что биноминальная куча - это не дерево, в котором есть k детей. Это дерево строго определено как

• Биномиальное дерево порядка 0 является одним узлом, и
• Биномиальное дерево порядка n - это один узел с биномиальными деревьями порядка 0, 1, 2, ..., n - 1 в качестве дочерних.

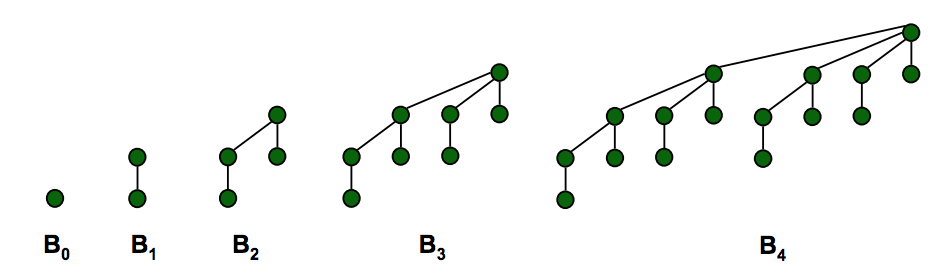
(Технически, особый случай порядка 0 здесь не нужен). Вы можете увидеть это здесь:

Обратите внимание, что существует ровно одно дерево каждого порядка, без какой-либо гибкости в отношении количества или расположения узлов.

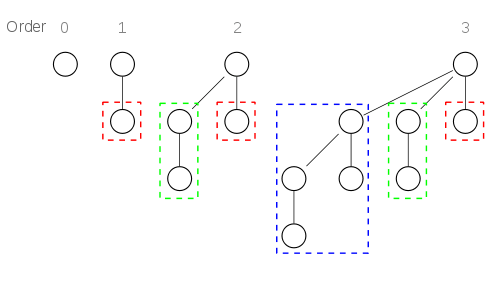
Тем не менее, важным альтернативным определением является следующее:

• Биномиальное дерево порядка 0 является одним узлом, и
• Биномиальное дерево порядка n - это два биномиальных дерева порядка n - 1, причем одно из деревьев стало дочерним для другого.

(Потратьте минуту, чтобы понять, почему они эквивалентны). Используя это второе определение, можно быстро доказать, что количество узлов в дереве равно 2ⁿ. В качестве базового случая, дерево порядка 0 имеет 2⁰ = 1 узел, как требуется. Для индуктивного шага, если у нас есть два дерева порядка n - 1, они вместе имеют 2^n-1 + 2^n-1 = 2ⁿ узлов, как требуется. Таким образом, общее количество узлов в биномиальном дереве порядка n равно 2ⁿ.

Идея кучи, которую вы описываете в своем последнем абзаце, не всегда приводит к эффективной среде выполнения. В частности, если у вас есть деревья с огромным фактором ветвления и без других структурных ограничений, то теоретически вы можете построить кучу из n узлов, состоящих из одного узла с (n - 1) дочерними элементами. В этом случае после удаления минимального элемента из кучи вам нужно будет просмотреть все n - 1 дочерних элементов, чтобы определить, какой был новый минимум, и дать время выполнения O(n). Другие структурные ограничения на деревья, такие как полные двоичные деревья, биномиальные деревья и т. Д., Гарантируют, что этого наихудшего случая не произойдет.

Надеюсь это поможет!

Answer 2

Двоичная куча может быть создана путем соединения любых двух дочерних полных двоичных деревьев одного ранга с корневым узлом. Это дерево с немного свободным стилем - некоторые листья можно вырезать справа

Биномиальное дерево ранга N не является лесом деревьев. Это корневой узел со связанными с ним биномиальными деревьями рангов N-1, N-2,...,1,0. Биноминальная куча - это дерево с абсолютно фиксированной структурой.

(Боюсь, кто-то неправильно прочитал Wiki.) У биномиального дерева порядка k есть корневой узел, чьи дети являются корнями биномиальных деревьев порядков k−1, k−2, ..., 2, 1, 0 (в этом порядке).

Answer 3

Добавить к большому ответу выше, предоставленному templatetypedef. Вот наглядная таблица, показывающая разную сложность времени для разных операций

╔══════════════╦═══════════════════════╦════════════════════════╗
║  Operation   ║       Binary          ║      Binomial          ║
╠══════════════╬═══════════════════════╬════════════════════════╣
║              ║                       ║                        ║                              
║   insert     ║      O(logN)          ║      O(logN)           ║
║              ║                       ║                        ║                              
╠══════════════╬═══════════════════════╬════════════════════════╣
║  find Min    ║       O(1)            ║      O(logN)           ║
║              ║                       ║                        ║
╠══════════════╬═══════════════════════╬════════════════════════╣
║              ║                       ║                        ║
║   Revmove    ║       O(logN)         ║      O(logN)           ║
║              ║                       ║                        ║
╠══════════════╬═══════════════════════╬════════════════════════╣
║              ║                       ║                        ║
║ Decrease Key ║       O(logN)         ║      O(logN)           ║
║              ║                       ║                        ║
╠══════════════╬═══════════════════════╬════════════════════════╣
║              ║                       ║                        ║
║    Union     ║         O(N)          ║      O(logN)           ║
║              ║                       ║                        ║
╠══════════════╬═══════════════════════╬════════════════════════╣
║              ║ ■ Min element is root ║order k binomial tree Bk║
║              ║ ■ Heap height = logN  ║ ■ Number of nodes = 2k.║
║              ║                       ║ ■ Height = k.          ║                  
║              ║                       ║ ■ Degree of root = k.  ║
║  Useful      ║                       ║ ■ Deleting root yields ║
║  Properties  ║                       ║   binomial trees       ║
║              ║                       ║   Bk-1, … , B0.        ║
║              ║                       ║   (see graph below)    ║
║              ║                       ║                        ║
║              ║                       ║                        ║
║              ║                       ║                        ║
║              ║                       ║                        ║        
╚══════════════╩═══════════════════════╩════════════════════════╝

Я получил это изображение из слайдов лекций Принстона

Binary Heap: (почти полное двоичное дерево)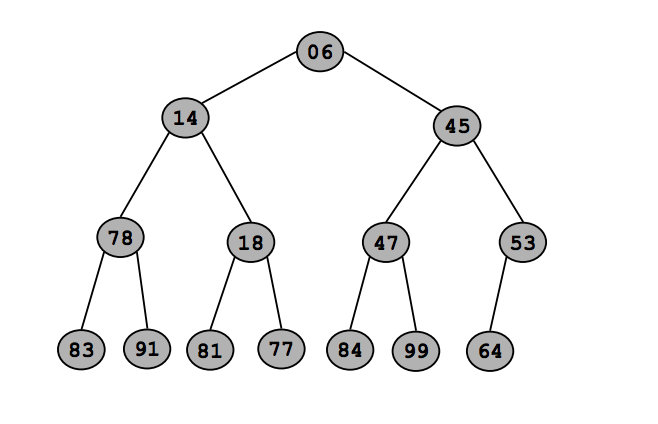

Биноминальная куча: