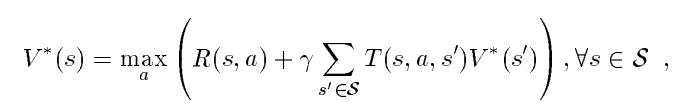Динамическое программирование процесса принятия решений Маркова с итерацией значения

Question

Я узнаю о MDPи value iteration в самообучении, и я надеюсь, что кто-то может улучшить мое понимание.

Рассмотрим проблему с 3-х сторонними кубиками, имеющими номера 1, 2, 3, Если вы бросаете 1 или 2 вы получаете это значение в $ но если вы бросите 3 вы теряете все свои деньги и игра заканчивается (finite horizon problem)

Концептуально я понимаю, как это сделать со следующим форумом:

Итак, давайте разберемся с этим:

Так как это finite horizon проблема, которую мы можем игнорировать gamma,

Если я observe 1Я могу либо go или же stop, utility/value из этого:

V(1) = max(Q(1, g), Q(1, s))
Q(1, g) = r + SUM( P( 2 | 1,g) * V(2) + P( 3 | 1,g) * V(3))
Q(1, s) = r + SUM( P( 2 | 1,s) * V(2) + P( 3 | 1,s) * V(3))

where r = 1

я observe 2Я могу либо go или же stop:

V(2) = max(Q(2, g), Q(2, s))
Q(2, g) = r + SUM( P( 1 | 2,g) * V(1) + P( 3 | 1,g) * V(3))
Q(2, s) = r + SUM( P( 1 | 2,s) * V(1) + P( 3 | 1,s) * V(3))

where r = 2

Я наблюдаю 3, игра заканчивается.

Наглядно V(3) является 0 потому что игра окончена, поэтому мы можем удалить эту половину из уравнения Q(1, g), Мы определили V(2) выше, так что мы можем заменить это как:

Q(1, g) = r + SUM( P( 2 | 1,g) *     
    MAX ((P( 1 | 2,g) * V(1)) , (P( 1 | 2,s) * V(1))))

Это где вещи принимают плохой оборот. Я не уверен, как решить Q(1, g) если оно имеет свое определение в своем решении. Это, вероятно, из-за плохого математического фона.

Что я понимаю, так это то, что коммунальные услуги или значения штатов будут меняться в зависимости от вознаграждения, и поэтому решение будет меняться.

В частности, если бросить три дал вам $3 пока игра заканчивается, это повлияет на ваше решение, поскольку утилита изменилась.

Но я не уверен, как написать код для расчета этого.

Может кто-нибудь объяснить, как работает динамическое программирование в этом? Как мне решить Q(1,g) или же Q(1,s) когда это в своем собственном определении?

Answer 1

Специальное решение:

Для вашего примера довольно легко узнать, следует ли выбирать "идти" или "остановить": есть денежная стоимость X для которых одинаково, идете ли вы "идти" или "останавливаться", для всех меньших значений вы должны "идти", для всех больших значений вы должны останавливаться. Итак, единственный вопрос, что это за значение:

X=E("stop"|X)=E("go"|X)=1/3(1+X)+1/3(2+x) =>
1/3X=1 =>
X=3

Уже в первой строке я использовал это, даже если я выберу "пойти" и выиграть, я выберу стоп в следующем раунде. Итак, зная, какое решение следует принять, легко рассчитать ожидаемый выигрыш с идеальной стратегией, здесь, в python:

def calc(money):
    PROB=1.0/3.0
    if money<3:#go
       return  PROB*calc(money+1)+PROB*calc(money+2)-PROB*0
    else:#stop
       return money 

print "Expected win:", calc(0)

>>> Expected win: 1.37037037037

---

Общее решение:

Я не уверен, что приведенный выше порядок действий можно обобщить для произвольных сценариев. Однако есть и другая возможность решить такие проблемы.

Давайте немного изменим игру: больше не бесконечно много ходов, но самое большее N получается. Тогда ваша рекурсия становится:

E(money, N)=max(money, 1/3*E(money+1, N-1)+1/3*E(money+1, N-1))

Как вы можете легко увидеть значение E(money, N) больше не зависит от себя, а от результатов игры с меньшим количеством ходов.

Без доказательств я утверждаю, что вы ищете E(money)=lim_{N->infinity} E(money, N),

Для вас особая проблема: код Python будет выглядеть следующим образом:

PROB=1.0/3.0

MAX_GOS=20#neglect all possibilities with more than 1000 decisions "GO"

LENGTH=2*MAX_GOS+1#per go 2$ are possible

#What is expected value if the game ended now?
expected=range(LENGTH)

for gos_left in range(1,MAX_GOS+1):
   next=[0]*len(expected)
   for money in range(LENGTH-gos_left*2):
       next[money]=max(expected[money], PROB*expected[money+1]+PROB*expected[money+2])#decision stop or go
   expected=next

print "Expected win:", expected[0]

>>> Expected win: 1.37037037037

Я рад, что оба метода дали одинаковый результат!