Могу ли я попросить физические аналогии или метафоры для рекурсии?
Я внезапно нахожусь в классе рекурсивного языка (sml), и рекурсия для меня еще не физически разумна. Я думаю о том, как пол квадратных плиток иногда является моделью или метафорой для целочисленного умножения, или жезлы Кюизенера являются моделью или аналогом для сложения и вычитания. У кого-нибудь есть такие модели, которыми вы могли бы поделиться?
5 ответов
Представьте, что вы настоящий волшебник и можете сделать себе копию. Вы создаете своего двойника на шаг ближе к цели и отдаете ему (или ей) те же приказы, что и вам.
Твой двойник делает то же самое со своей копией. Видишь ли, он тоже волшебник.
Когда окончательная копия оказывается созданной у цели, ей больше некуда идти, поэтому она сообщает об этом своему создателю. Который делает то же самое.
В конце концов, вы получите ответ - не сдвинувшись ни на дюйм - и теперь сможете легко получить из него конечный результат. Вы притворяетесь, что не знаете, что все эти двойники делают за вас тяжелую работу. "Хм, - говорите вы себе, - что, если бы я был на шаг ближе к цели и уже знал результат? Не будет ли тогда легко найти окончательный ответ ?" *
Конечно, если бы вы были двойником, вам бы пришлось сообщить о своих выводах вашему создателю.
Больше здесь.
(также, я думаю, что я видел это событие "создания двойников" здесь, хотя я не совсем уверен).
* и в этом суть рекурсивного метода решения проблем.
Как я знаю, что моя процедура правильная? Если мой простой маленький шаг комбинации дает правильное решение, в предположении, что он дал правильное решение для меньшего случая, все, что мне нужно, это убедиться, что он работает для наименьшего случая - базового случая - и затем по индукции доказанность доказана!
Другая возможность - " разделяй и властвуй", где мы разбиваем нашу задачу на две половины, поэтому гораздо быстрее доберемся до базового варианта. Пока шаг комбинации прост (и, конечно, сохраняет обоснованность решения), он работает. В нашей метафоре фокусника я получаю две копии себя и объединяю их два ответа в один, когда они закончены. Каждый из них также создает две свои копии, так что это создает ветвящееся дерево магов вместо простой линии, как раньше.
Хорошим примером является треугольник Серпинского, который представляет собой фигуру, которая построена из трех треугольников Серпинского размером с четверть, просто сложив их по углам.
Каждый из трех составных треугольников построен по одному рецепту.
Хотя у него нет базового случая, и поэтому рекурсия не ограничена (бездонный; бесконечный), любое конечное представление ST, вероятно, нарисует просто точку вместо ST, которая слишком мала (служит в качестве базового случая, останавливая рекурсия).
Хорошая картина этого есть в связанной статье в Википедии.
Рекурсивное рисование ST без ограничения размера никогда не будет ничего рисовать на экране! Для математиков рекурсия может быть отличной, но инженеры должны быть осторожнее с ней.:)
Переключаясь на итерацию corecursion (см. Связанный ответ), мы сначала нарисуем контуры, а затем интерьеры; так что даже без ограничения размера картинка будет выглядеть довольно быстро. Программа тогда будет занята без какого-либо заметного эффекта, но это лучше, чем пустой экран.
Я наткнулся на это произведение от Эдсгера В. Дейкстры; он рассказывает, как его ребенок схватил рекурсии:
Через несколько лет пятилетний сын покажет мне, как плавно приходит мысль о рекурсии. Гуляя со мной по центру города, он вдруг заметил мне, папа, не у каждой лодки есть спасательная шлюпка, не так ли? Я сказал, как прийти? Ну, спасательная шлюпка могла бы иметь меньшую спасательную шлюпку, но тогда это было бы без нее.
Я люблю этот вопрос и не могу удержаться, чтобы добавить ответ...
Рекурсия - русская кукла программирования. Первый пример, который мне приходит в голову, ближе к примеру взаимной рекурсии:
Взаимная рекурсия повседневный пример
Взаимная рекурсия - это частный случай рекурсии (но иногда легче понять из конкретного случая, чем из общего), когда у нас есть две функции A а также B определяется как A звонки B а также B звонки A, Вы можете очень легко экспериментировать с веб-камерой (она также работает с 2 зеркалами):
- отобразить вывод веб-камеры на экране с помощью VLC или любого программного обеспечения, которое может это сделать.
- Направьте свою веб-камеру на экран.
- Экран будет постепенно отображать бесконечный "вихрь" экрана.
Что просходит?
- Веб-камера (
A) захватить экран (B) - На экране отображается изображение, снятое веб-камерой (сам экран).
- Веб-камера захватывает экран с отображенным на нем экраном.
- Экран отображает это изображение (теперь отображаются два экрана)
- И так далее.
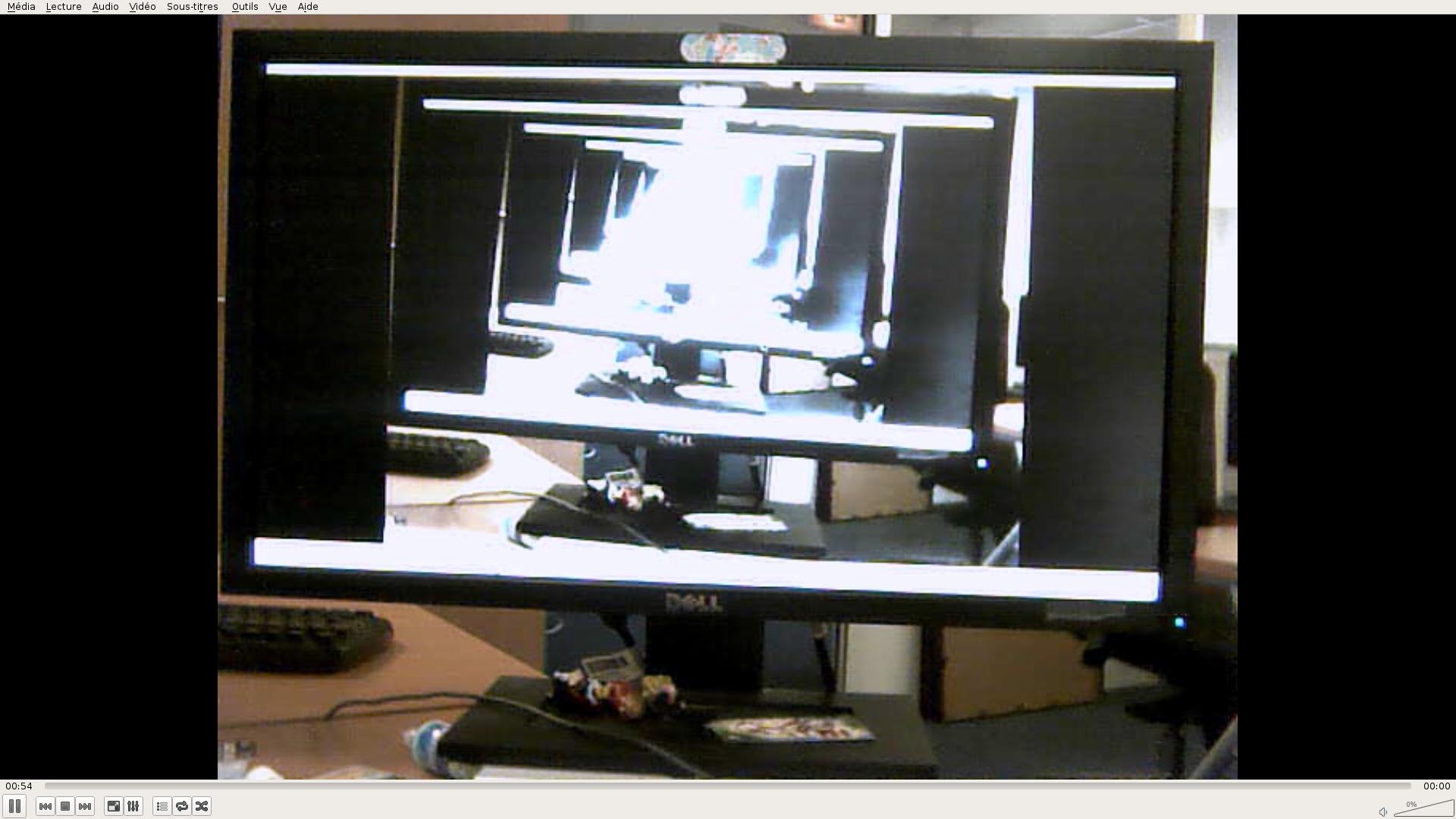
Вы, наконец, в конечном итоге с таким изображением (да, моя веб-камера полная чушь):
"Простая" рекурсия более или менее одинакова, за исключением того, что существует только один субъект (функция), который вызывает себя (A звонки A)
"Простая" рекурсия
Это более или менее тот же ответ, что и @WillNess, но с небольшим количеством кода и некоторой интерактивностью (используя фрагменты js SO)
Допустим, вы очень мотивированный золотоискатель, ищущий золото, с очень крошечной шахтой, настолько маленькой, что вы можете искать золото только по вертикали. И поэтому вы копаете, и вы проверяете на золото. Если вы найдете что-нибудь, вам больше не нужно копать, просто возьмите золото и уходите. Но если вы этого не сделаете, это означает, что вы должны копать глубже. Таким образом, есть только две вещи, которые могут остановить вас:
- В поисках золотого самородка.
- Земное кипящее ядро из расплавленного железа.
Так что, если вы хотите написать это программно, используя рекурсию, это может быть что-то вроде этого:
// This function only generates a probability of 1/10
function checkForGold() {
let rnd = Math.round(Math.random() * 10);
return rnd === 1;
}
function digUntilYouFind() {
if (checkForGold()) {
return 1; // he found something, no need to dig deeper
}
// gold not found, digging deeper
return digUntilYouFind();
}
let gold = digUntilYouFind();
console.log(`${gold} nugget found`);
Или немного больше интерактивности:
// This function only generates a probability of 1/10
function checkForGold() {
console.log("checking...");
let rnd = Math.round(Math.random() * 10);
return rnd === 1;
}
function digUntilYouFind() {
if (checkForGold()) {
console.log("OMG, I found something !")
return 1;
}
try {
console.log("digging...");
return digUntilYouFind();
} finally {
console.log("climbing back...");
}
}
let gold = digUntilYouFind();
console.log(`${gold} nugget found`);Если мы не найдем немного золота, digUntilYouFind Функция вызывает сама. Когда майнер "лезет обратно" из своей шахты, это на самом деле самый глубокий дочерний вызов функции, возвращающей золотой самородок через всех его родителей (стек вызовов) до тех пор, пока значение не будет присвоено gold переменная.
Здесь вероятность достаточно высока, чтобы майнер не копался в земном ядре. Ядро земли для майнера - это размер стека для программы. Когда майнер приходит к ядру, он умирает от ужасной боли, когда программа превышает размер стека (вызывает переполнение стека), она падает.
Компилятор / интерпретатор может выполнить оптимизацию, чтобы обеспечить бесконечный уровень рекурсии, такой как оптимизация хвостового вызова.
Это странный и не совсем физический пример, за исключением того, что танцевальное движение является физическим. Это произошло со мной на следующее утро. Я называю это "Написано на латыни, решено на иврите". А? Конечно, вы говорите "А?"
Под этим я подразумеваю, что кодирование рекурсии обычно выполняется слева направо в стиле латинского алфавита: "Def fac(n) = n*(fac(n-1))". Стиль движения - "крайний случай к базовому случаю".
Но (пожалуйста, отметьте это), по крайней мере, в этом простом случае кажется, что самый простой способ оценить его - справа налево, в стиле ивритского алфавита: начните с базового варианта и переместитесь наружу в крайний случай:
(fac(0) = 1)
(fac(1) = 1)*(fac(0) = 1)
(fac(2))*(fac(1) = 1)*(fac(0) = 1)
(fac(n)*(fac(n-1)*...*(fac(2))*(fac(1) = 1)*(fac(0) = 1)
(* Easier order to calculate <<<<<<<<<<< is leftwards,
base outwards to outermost case;
more difficult order to calculate >>>>>> is rightwards,
outermost case to base *)
Тогда вам не придется приостанавливать элементы слева, пока вы ожидаете результатов вычислений справа. "Танцуй влево" вместо "Танцуй вправо"?
Воспринимайте фракталы как рекурсивные: каждый раз применяется один и тот же шаблон, но каждая фигура отличается от другой.
В качестве природных явлений с фрактальными особенностями Википедия представляет:
- Маунтин Рейндж
- Морозные кристаллы
- ДНК
- и даже белки.