Как решить это с помощью простого алгоритма вперед-назад?
Я играл с алгоритмом прямого-обратного хода, чтобы найти наиболее эффективный (определяемый функцией стоимости, зависящей от того, как текущее состояние отличается от следующего состояния) путь для перехода из состояния 1 в состояние N. На рисунке ниже краткая версия проблемы может быть замечена только с 3 государствами и 2 узлами на государство. Я делаю вперед-назад алгоритм на этом и нахожу лучший путь, как обычно. Красные биты на изображениях - это пути, проверенные во время бита прямого распространения в коде.
Теперь интересный момент, теперь я хочу найти лучший путь с 3 состояниями (как и раньше), но теперь известны только узлы в первом состоянии. Остальные 4 в настоящее время находятся в свободном обращении и могут рассматриваться как находящиеся в любом штате (штат 2 или штат 3). Я хочу знать, есть ли у вас, ребята, хорошая идея, как это сделать.
Изображение: https://i.imgur.com/JrQ2tul.jpg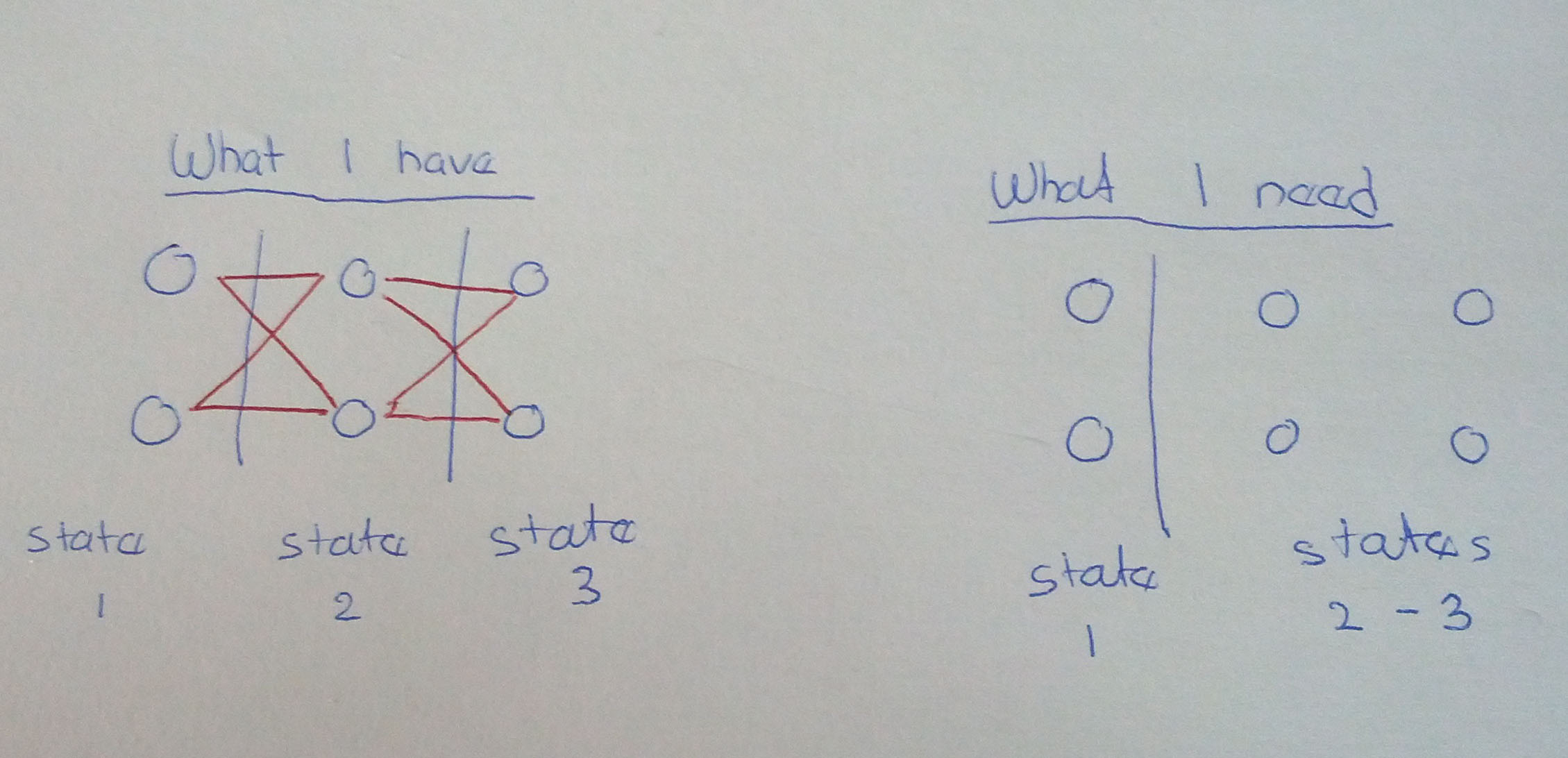
Примечание. Имейте в виду, что исходная проблема состоит из примерно 25 штатов и 100 узлов на штат. Таким образом, вы будете знать состояние около 100 узлов в состоянии 1, но остальные 24*100 узлов не будут иметь состояния. В этом случае я хочу найти путь длиной в 25 состояний (с минимальными затратами).
Приложение: Кто-то указал, что лучшим алгоритмом был бы алгоритм Витерби. Итак, вот проблема с добавлением большего количества переменных. Не могли бы вы, ребята, объяснить, как это будет реализовано? Применяются те же правила, путь должен начинаться с одного из узлов в состоянии 1 (узел а или узел b). Кроме того, функция стоимости, использующая норму, не имеет смысла в этом случае, так как у нас есть только одно свойство (размер узла), но в реальной задаче я ожидаю намного больше свойств.
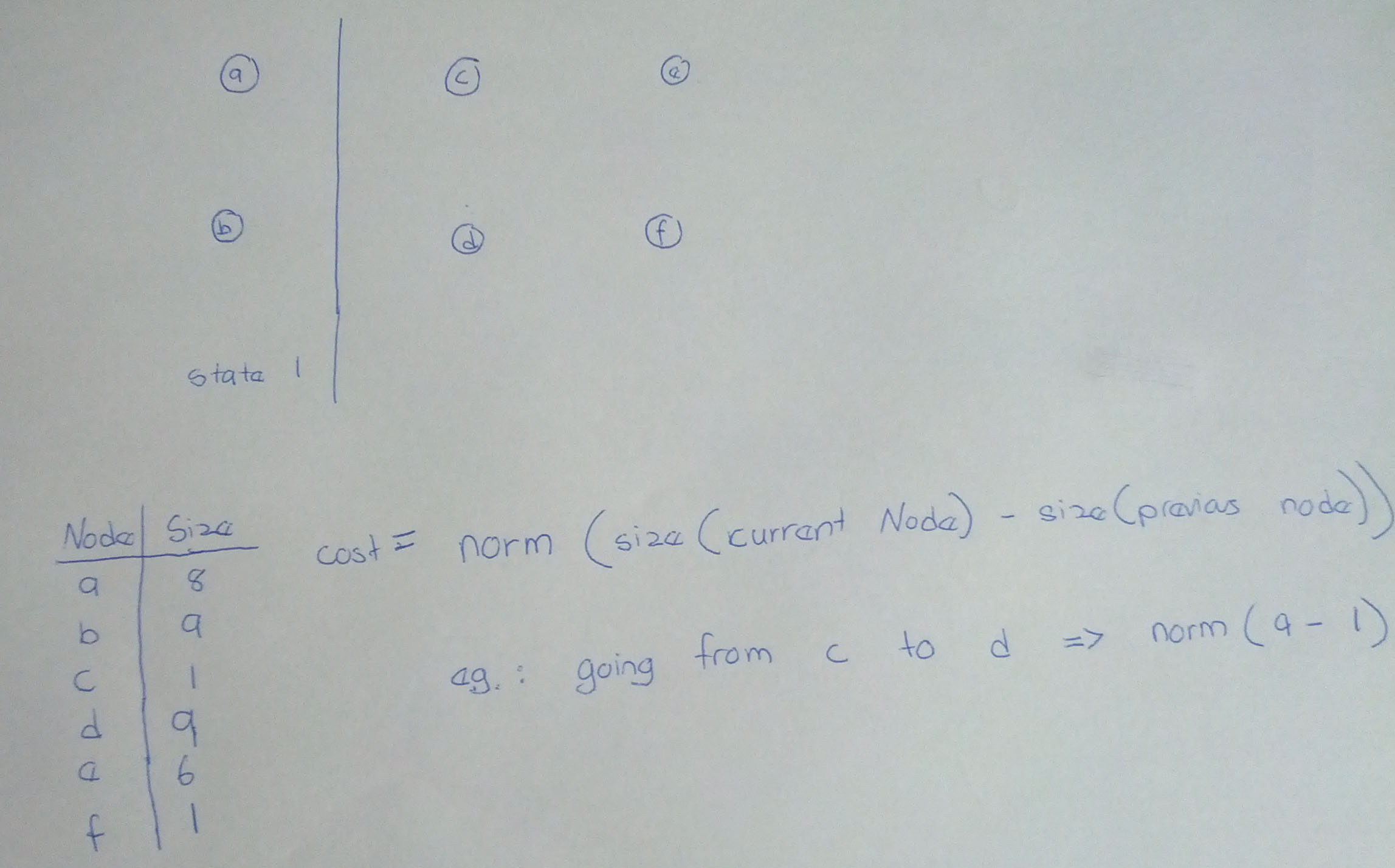
1 ответ
Вариант алгоритма Дейкстры может быть быстрее для вашей задачи, чем алгоритм прямого-обратного, потому что он не анализирует все узлы одновременно. В конце концов, Дейкстра - это алгоритм ДП.
Пусть узел будет указан
Node:
Predecessor : Node
Total cost : Number
Visited nodes : Set of nodes (e.g. a hash set or other performant set)
Инициализировать алгоритм с
open set : ordered (by total cost) set of nodes = set of possible start nodes (set visitedNodes to the one-element set with the current node)
( = {a, b} in your example)
Затем выполните алгоритм:
do
n := pop element from open set
if(n.visitedNodes.count == stepTarget)
we're done, backtrace the path from this node
else
for each n2 in available nodes
if not n2 in n.visitedNodes
push copy of n2 to open set (the same node might appear multiple times in the set):
.cost := n.totalCost + norm(n2 - n)
.visitedNodes := n.visitedNodes u { n2 } //u = set union
.predecessor := n
next
loop
Если вычисление нормы стоит дорого, вы можете рассчитать его по требованию и сохранить на карте.