Как применить вейвлеты Габора к изображению?

Question

Как применить эти вейвлеты фильтра Габора к изображению?

close all;
clear all;
clc;

% Parameter Setting
R = 128;
C = 128;
Kmax = pi / 2;
f = sqrt( 2 );
Delt = 2 * pi;
Delt2 = Delt * Delt;

% Show the Gabor Wavelets
for v = 0 : 4
    for u = 1 : 8
        GW = GaborWavelet ( R, C, Kmax, f, u, v, Delt2 ); % Create the Gabor wavelets
          figure( 2 );
     subplot( 5, 8, v * 8 + u ),imshow ( real( GW ) ,[]); % Show the real part of Gabor wavelets

    end

    figure ( 3 );
     subplot( 1, 5, v + 1 ),imshow ( abs( GW ),[]); % Show the magnitude of Gabor wavelets

end



function GW = GaborWavelet (R, C, Kmax, f, u, v, Delt2)


k = ( Kmax / ( f ^ v ) ) * exp( 1i * u * pi / 8 );% Wave Vector

kn2 = ( abs( k ) ) ^ 2;

GW = zeros ( R , C );

for m = -R/2 + 1 : R/2

    for n = -C/2 + 1 : C/2

        GW(m+R/2,n+C/2) = ( kn2 / Delt2 ) * exp( -0.5 * kn2 * ( m ^ 2 + n ^ 2 ) / Delt2) * ( exp( 1i * ( real( k ) * m + imag ( k ) * n ) ) - exp ( -0.5 * Delt2 ) );

    end

end

Изменить: это размеры моего изображения

Answer 1

Типичное использование фильтров Габора - это расчет откликов фильтра в каждой из нескольких ориентаций, например, для обнаружения края.

Вы можете свертывать фильтр с изображением, используя теорему о свертке, взяв обратное преобразование Фурье поэлементного произведения преобразований Фурье изображения и фильтра. Вот основная формула:

%# Our image needs to be 2D (grayscale)
if ndims(img) > 2;
    img = rgb2gray(img);
end
%# It is also best if the image has double precision
img = im2double(img);

[m,n] = size(img);
[mf,nf] = size(GW);
GW = padarray(GW,[n-nf m-mf]/2);
GW = ifftshift(GW);
imgf = ifft2( fft2(img) .* GW );

Как правило, свертка FFT лучше для ядер размером> 20. Для деталей, я рекомендую Числовые Рецепты в C, у которого есть хорошее, независимое от языка описание метода и его предостережений.

Ваши ядра уже большие, но с помощью метода FFT они могут быть такими же большими, как изображение, поскольку они дополняются до этого размера независимо. Из-за периодичности БПФ способ выполняет циклическую свертку. Это означает, что фильтр будет обтекать границы изображения, поэтому мы должны также дополнить само изображение, чтобы устранить этот краевой эффект. Наконец, поскольку мы хотим получить общий отклик на все фильтры (по крайней мере, в типичной реализации), нам нужно поочередно применить каждый к изображению и суммировать ответы. Обычно используется только от 3 до 6 ориентаций, но также обычно выполняется фильтрация в нескольких масштабах (при разных размерах ядра), поэтому в этом контексте используется большее количество фильтров.

Вы можете сделать все это с помощью кода следующим образом:

img = im2double(rgb2gray(img)); %# 
[m,n] = size(img); %# Store the original size.

%# It is best if the filter size is odd, so it has a discrete center.
R = 127; C = 127;

%# The minimum amount of padding is just "one side" of the filter.
%# We add 1 if the image size is odd.
%# This assumes the filter size is odd.
pR = (R-1)/2;
pC = (C-1)/2;
if rem(m,2) ~= 0; pR = pR + 1; end;
if rem(n,2) ~= 0; pC = pC + 1; end;
img = padarray(img,[pR pC],'pre'); %# Pad image to handle circular convolution.

GW = {}; %# First, construct the filter bank.
for v = 0 : 4
    for u = 1 : 8
        GW =  [GW {GaborWavelet(R, C, Kmax, f, u, v, Delt2)}];
    end
end

%# Pad all the filters to size of padded image.
%# We made sure padsize will only be even, so we can divide by 2.
padsize = size(img) - [R C];
GW = cellfun( ...
        @(x) padarray(x,padsize/2), ...
        GW, ...
        'UniformOutput',false);

imgFFT = fft2(img); %# Pre-calculate image FFT.

for i=1:length(GW)
    filter = fft2( ifftshift( GW{i} ) ); %# See Numerical Recipes.
    imgfilt{i} = ifft2( imgFFT .* filter ); %# Apply Convolution Theorem.
end

%# Sum the responses to each filter. Do it in the above loop to save some space.
imgS = zeros(m,n);
for i=1:length(imgfilt)
    imgS = imgS + imgfilt{i}(pR+1:end,pC+1:end); %# Just use the valid part.
end

%# Look at the result.
imagesc(abs(imgS));

Имейте в виду, что это по сути минимальная реализация. Вы можете выбрать заполнение дубликатами границ вместо нулей, применить функцию оконного изображения к изображению или увеличить размер пэда, чтобы получить разрешение по частоте. Каждый из них является стандартным дополнением к методике, которую я изложил выше, и должен быть тривиален для исследований через Google и Wikipedia. Также обратите внимание, что я не добавил никаких базовых оптимизаций MATLAB, таких как предварительное распределение и т. Д.

В заключение, вы можете пропустить заполнение изображения (т.е. использовать первый пример кода), если ваши фильтры всегда намного меньше, чем изображение. Это связано с тем, что добавление нулей к изображению создает элемент искусственного края, с которого начинается заполнение. Если фильтр невелик, переход от круговой свертки не вызывает проблем, потому что будут задействованы только нули в заполнении фильтра. Но как только фильтр станет достаточно большим, эффект оборачивания станет серьезным. Если вам нужно использовать большие фильтры, вам, возможно, придется использовать более сложную схему заполнения или обрезать края изображения.

Answer 2

Чтобы "применить" вейвлет к изображению, вы обычно берете внутренний продукт вейвлета и изображение, чтобы получить единственное число, величина которого показывает, насколько этот вейвлет имеет отношение к изображению. Если у вас есть полный набор вейвлетов (так называемый "ортонормированный базис") для изображения из 128 строк и 128 столбцов, у вас будет 128*128 = 16 384 разных вейвлетов. У вас здесь только 40, но вы работаете с тем, что имеете.

Чтобы получить коэффициент вейвлета, вы можете сделать снимок, скажем так:

t = linspace(-6*pi,6*pi,128);
myImg = sin(t)'*cos(t) + sin(t/3)'*cos(t/3);

и возьмите внутреннее произведение этого и одного из базисных векторов GW следующим образом:

myCoef = GW(:)'*myImg(:);

Мне нравится складывать все мои вейвлеты в матрицу GW_ALL, где каждая строка является одним из 32-ваттных (:)) вейвлетов, а затем вычислять все коэффициенты вейвлета одновременно, записывая

waveletCoefficients = GW_ALL*myImg(:);

Если вы построите их с помощью стебля (abs(waveletCoefficients)), вы заметите, что некоторые из них больше других. Большие значения - это те, которые соответствуют изображению.

Наконец, предполагая, что ваши вейвлеты ортогональны (на самом деле это не так, но это не очень важно здесь), вы можете попытаться воспроизвести изображение с помощью ваших вейвлетов, но имейте в виду, что у вас есть только 32 из всех возможностей, и они все на центр изображения... поэтому, когда мы пишем

newImage = real(GW_ALL'*waveletCoefficients);

мы получаем нечто похожее на исходное изображение в центре, но не снаружи.

Я добавил в ваш код (ниже), чтобы получить следующие результаты: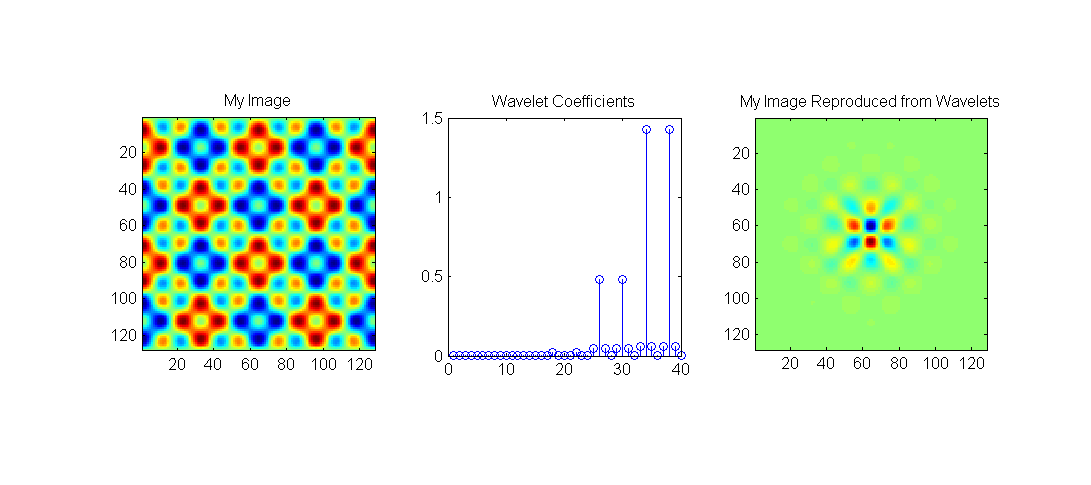

Где модификации:

% function gaborTest()

close all;
clear all;
clc;

% Parameter Setting
R = 128;
C = 128;
Kmax = pi / 2;
f = sqrt( 2 );
Delt = 2 * pi;
Delt2 = Delt * Delt;

% GW_ALL = nan(32, C*R);

% Show the Gabor Wavelets
for v = 0 : 4
    for u = 1 : 8
        GW = GaborWavelet ( R, C, Kmax, f, u, v, Delt2 ); % Create the Gabor wavelets
          figure( 2 );
         subplot( 5, 8, v * 8 + u ),imshow ( real( GW ) ,[]); % Show the real part of Gabor wavelets

         GW_ALL( v*8+u, :) = GW(:);

    end

    figure ( 3 );
     subplot( 1, 5, v + 1 ),imshow ( abs( GW ),[]); % Show the magnitude of Gabor wavelets

end

%% Create an Image:
t = linspace(-6*pi,6*pi,128);
myImg = sin(t)'*cos(t) + sin(t/3)'*cos(t/3);
figure(3333);
clf
subplot(1,3,1);
imagesc(myImg);
title('My Image');
axis image

%% Get the coefficients of the wavelets and plot:
waveletCoefficients = GW_ALL*myImg(:);

subplot(1,3,2);
stem(abs(waveletCoefficients));
title('Wavelet Coefficients')

%% Try and recreate the image from just a few wavelets.
% (we would need C*R wavelets to recreate perfectly)

subplot(1,3,3);
imagesc(reshape(real(GW_ALL'*waveletCoefficients),128,128))
title('My Image Reproduced from Wavelets');
axis image

Этот подход формирует основу для извлечения вейвлет-коэффициентов и воспроизведения изображения. Вейвлеты Габора (как уже отмечалось) не являются ортогональными ( эталонными) и с большей вероятностью будут использоваться для извлечения признаков с использованием свертки, как описано в reve_etrange. В этом случае вы можете добавить это в свой внутренний цикл:

 figure(34);
 subplot(5,8, v * 8 + u );
 imagesc(abs(ifft2((fft2(GW).*fft2(myImg)))));
 axis off