Обратимые STFT и ISTFT в Python
Существует ли какая-либо универсальная форма кратковременного преобразования Фурье с соответствующим обратным преобразованием, встроенным в SciPy, NumPy или что-то еще?
Там есть пиплот specgram функция в matplotlib, которая вызывает ax.specgram(), который вызывает mlab.specgram(), который вызывает _spectral_helper():
#The checks for if y is x are so that we can use the same function to #implement the core of psd(), csd(), and spectrogram() without doing #extra calculations. We return the unaveraged Pxy, freqs, and t.
но
Это вспомогательная функция, которая реализует общность между 204 #psd, csd и спектрограммой. Это НЕ предназначено для использования за пределами Mlab
Я не уверен, что это можно использовать для выполнения STFT и ISTFT. Есть ли что-нибудь еще, или я должен перевести что-то вроде этих функций MATLAB?
Я знаю, как написать свою собственную специальную реализацию; Я просто ищу что-то полнофункциональное, которое может обрабатывать различные оконные функции (но имеет нормальное значение по умолчанию), полностью обратимо с окнами COLA (istft(stft(x))==x), проверено множеством людей, нет ошибок, связанных с ошибками, хорошо обрабатывает концы и заполнение нулями, быстрая реализация RFFT для реального ввода и т. д.
11 ответов
Я немного опоздал с этим, но понял, что у Сципи есть встроенная функция istft с 0.19.0
Вот мой код Python, упрощенный для этого ответа:
import scipy, pylab
def stft(x, fs, framesz, hop):
framesamp = int(framesz*fs)
hopsamp = int(hop*fs)
w = scipy.hanning(framesamp)
X = scipy.array([scipy.fft(w*x[i:i+framesamp])
for i in range(0, len(x)-framesamp, hopsamp)])
return X
def istft(X, fs, T, hop):
x = scipy.zeros(T*fs)
framesamp = X.shape[1]
hopsamp = int(hop*fs)
for n,i in enumerate(range(0, len(x)-framesamp, hopsamp)):
x[i:i+framesamp] += scipy.real(scipy.ifft(X[n]))
return x
Заметки:
- Понимание списка - это небольшая хитрость, которую я хотел бы использовать для симуляции блочной обработки сигналов в numpy/scipy. Это как
blkprocв Matlab. Вместоforцикл, я применяю команду (например,fft) к каждому кадру сигнала внутри понимания списка, а затемscipy.arrayбросает его в 2D-массив. Я использую это для создания спектрограмм, хроматограмм, MFCC-грамм и многого другого. - Для этого примера я использую наивный метод наложения и добавления в
istft, Чтобы восстановить исходный сигнал, сумма последовательных оконных функций должна быть постоянной, предпочтительно равной единице (1,0). В этом случае я выбрал Ханна (илиhanning) окно и перекрытие 50%, которое работает отлично. Смотрите это обсуждение для получения дополнительной информации. - Вероятно, существуют более принципиальные способы вычисления ISTFT. Этот пример в основном предназначен для образования.
Тест:
if __name__ == '__main__':
f0 = 440 # Compute the STFT of a 440 Hz sinusoid
fs = 8000 # sampled at 8 kHz
T = 5 # lasting 5 seconds
framesz = 0.050 # with a frame size of 50 milliseconds
hop = 0.025 # and hop size of 25 milliseconds.
# Create test signal and STFT.
t = scipy.linspace(0, T, T*fs, endpoint=False)
x = scipy.sin(2*scipy.pi*f0*t)
X = stft(x, fs, framesz, hop)
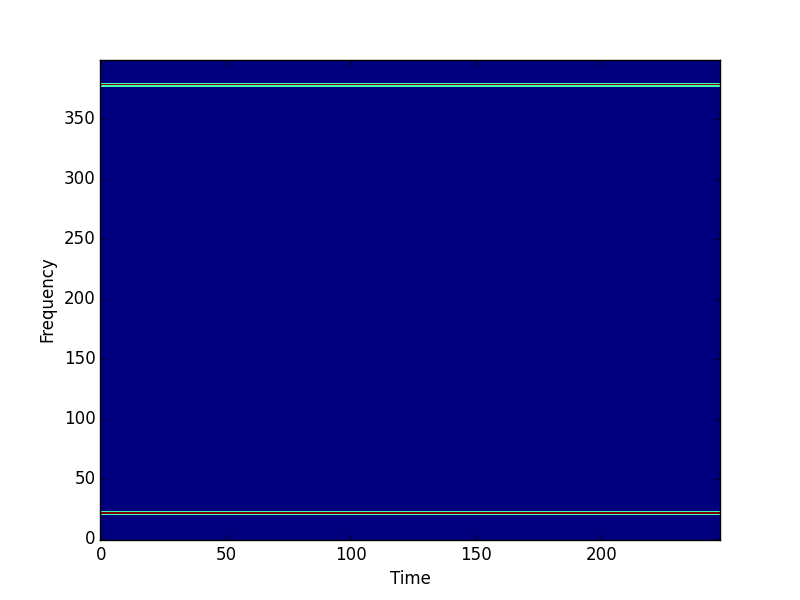
# Plot the magnitude spectrogram.
pylab.figure()
pylab.imshow(scipy.absolute(X.T), origin='lower', aspect='auto',
interpolation='nearest')
pylab.xlabel('Time')
pylab.ylabel('Frequency')
pylab.show()
# Compute the ISTFT.
xhat = istft(X, fs, T, hop)
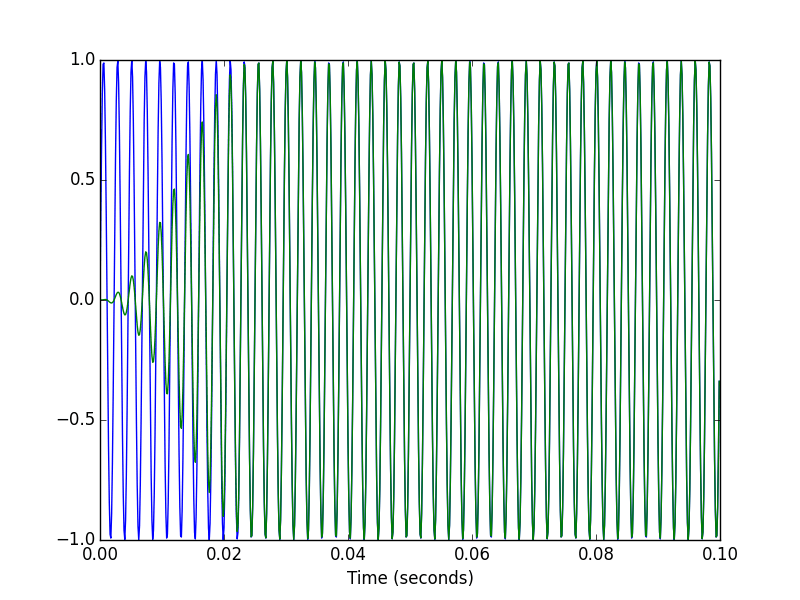
# Plot the input and output signals over 0.1 seconds.
T1 = int(0.1*fs)
pylab.figure()
pylab.plot(t[:T1], x[:T1], t[:T1], xhat[:T1])
pylab.xlabel('Time (seconds)')
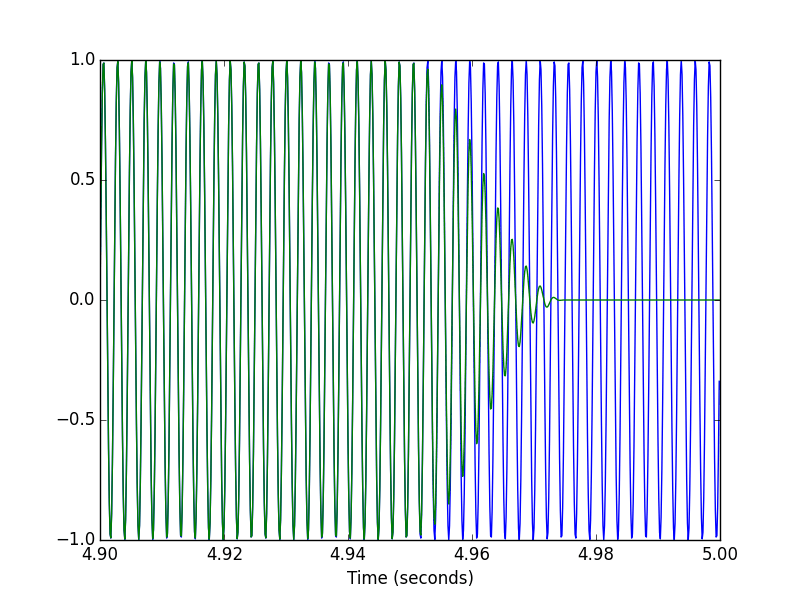
pylab.figure()
pylab.plot(t[-T1:], x[-T1:], t[-T1:], xhat[-T1:])
pylab.xlabel('Time (seconds)')
Вот код STFT, который я использую. STFT + ISTFT здесь дает идеальную реконструкцию (даже для первых кадров). Я немного изменил код, приведенный здесь Стивом Тджоа: здесь величина восстановленного сигнала такая же, как у входного сигнала.
import scipy, numpy as np
def stft(x, fftsize=1024, overlap=4):
hop = fftsize / overlap
w = scipy.hanning(fftsize+1)[:-1] # better reconstruction with this trick +1)[:-1]
return np.array([np.fft.rfft(w*x[i:i+fftsize]) for i in range(0, len(x)-fftsize, hop)])
def istft(X, overlap=4):
fftsize=(X.shape[1]-1)*2
hop = fftsize / overlap
w = scipy.hanning(fftsize+1)[:-1]
x = scipy.zeros(X.shape[0]*hop)
wsum = scipy.zeros(X.shape[0]*hop)
for n,i in enumerate(range(0, len(x)-fftsize, hop)):
x[i:i+fftsize] += scipy.real(np.fft.irfft(X[n])) * w # overlap-add
wsum[i:i+fftsize] += w ** 2.
pos = wsum != 0
x[pos] /= wsum[pos]
return x
librosa.core.stft а также istft выглядеть очень похоже на то, что я искал, хотя они не существовали в то время:
librosa.core.stft(y, n_fft=2048, hop_length=None, win_length=None, window=None, center=True, dtype=<type 'numpy.complex64'>)
Они не инвертируют точно, хотя; концы сужаются.
Найден другой STFT, но нет соответствующей обратной функции:
http://code.google.com/p/pytfd/source/browse/trunk/pytfd/stft.py
def stft(x, w, L=None):
...
return X_stft
- w является оконной функцией в виде массива
- L - перекрытие, в образцах
Ни один из вышеперечисленных ответов не работал хорошо OOTB для меня. Поэтому я модифицировал Стива Тджоа.
import scipy, pylab
import numpy as np
def stft(x, fs, framesz, hop):
"""
x - signal
fs - sample rate
framesz - frame size
hop - hop size (frame size = overlap + hop size)
"""
framesamp = int(framesz*fs)
hopsamp = int(hop*fs)
w = scipy.hamming(framesamp)
X = scipy.array([scipy.fft(w*x[i:i+framesamp])
for i in range(0, len(x)-framesamp, hopsamp)])
return X
def istft(X, fs, T, hop):
""" T - signal length """
length = T*fs
x = scipy.zeros(T*fs)
framesamp = X.shape[1]
hopsamp = int(hop*fs)
for n,i in enumerate(range(0, len(x)-framesamp, hopsamp)):
x[i:i+framesamp] += scipy.real(scipy.ifft(X[n]))
# calculate the inverse envelope to scale results at the ends.
env = scipy.zeros(T*fs)
w = scipy.hamming(framesamp)
for i in range(0, len(x)-framesamp, hopsamp):
env[i:i+framesamp] += w
env[-(length%hopsamp):] += w[-(length%hopsamp):]
env = np.maximum(env, .01)
return x/env # right side is still a little messed up...
Исправленная версия ответа Баса.
import scipy, numpy as np
import matplotlib.pyplot as plt
def stft(x, fftsize=1024, overlap=4):
hop=fftsize//overlap
w = scipy.hanning(fftsize+1)[:-1] # better reconstruction with this trick +1)[:-1]
return np.vstack([np.fft.rfft(w*x[i:i+fftsize]) for i in range(0, len(x)-fftsize, hop)])
def istft(X, overlap=4):
fftsize=(X.shape[1]-1)*2
hop=fftsize//overlap
w=scipy.hanning(fftsize+1)[:-1]
rcs=int(np.ceil(float(X.shape[0])/float(overlap)))*fftsize
print(rcs)
x=np.zeros(rcs)
wsum=np.zeros(rcs)
for n,i in zip(X,range(0,len(X)*hop,hop)):
l=len(x[i:i+fftsize])
x[i:i+fftsize] += np.fft.irfft(n).real[:l] # overlap-add
wsum[i:i+fftsize] += w[:l]
pos = wsum != 0
x[pos] /= wsum[pos]
return x
a=np.random.random((65536))
b=istft(stft(a))
plt.plot(range(len(a)),a,range(len(b)),b)
plt.show()
Я также нашел это на GitHub, но он работает на конвейерах вместо обычных массивов:
http://github.com/ronw/frontend/blob/master/basic.py
def STFT(nfft, nwin=None, nhop=None, winfun=np.hanning):
...
return dataprocessor.Pipeline(Framer(nwin, nhop), Window(winfun),
RFFT(nfft))
def ISTFT(nfft, nwin=None, nhop=None, winfun=np.hanning):
...
return dataprocessor.Pipeline(IRFFT(nfft), Window(winfun),
OverlapAdd(nwin, nhop))
Просто поделись моим решением
импорт
import numpy as np
import matplotlib.pyplot as plt
определить прямые и обратные функции БПФ
def next_pow2(x):
return int(np.ceil(np.log(x)/np.log(2)))
def stft(x, w_length, w_shift, nfft=None, window=np.hanning):
w = window(w_length)
x_length = x.shape[0]
nfft = nfft if nfft else 2 ** next_pow2(w_length)
assert nfft >= w_length
n_step = 1
n_pad = w_length - x_length
if x_length > w_length:
n_step += int(np.ceil((x_length - w_length) / w_shift))
n_tail = np.mod((x_length - w_length), w_shift)
n_pad = w_shift - n_tail if n_tail > 0 else 0
x_padded = np.pad(x, [0, n_pad])
y = np.empty((n_step, nfft), dtype="complex")
for n in range(0, n_step):
n_start = n * w_shift
n_end = n_start + w_length
y[n] = np.fft.fft(w * x[n_start:n_end], nfft)
return y
def istft(x, w_length, w_shift, window):
n_overlap = w_length - w_shift
w = window(w_length)
x_length = w_length + (x.shape[0] - 1) * w_shift
y = np.zeros(x_length, dtype="float")
window_fix = np.zeros(x_length, dtype="float")
for _n, _s in enumerate(x):
n_start = _n * w_shift
n_end = n_start + w_length
x_ifft = np.real(np.fft.ifft(_s)[:w_length])
if _n == 0:
y[n_start:n_end] = x_ifft
window_fix[n_start:n_end] = w
else:
n_end_overlap = n_start + n_overlap
y[n_start:n_end_overlap] = 0.5 * (y[n_start:n_end_overlap] + x_ifft[:n_overlap])
y[n_end_overlap:n_end] = x_ifft[n_overlap:]
window_fix[n_start:n_end_overlap] = 0.5 * (window_fix[n_start:n_end_overlap] + w[:n_overlap])
window_fix[n_end_overlap:n_end] = w[n_overlap:]
w_non_zero = window_fix != 0
y[w_non_zero] = y[w_non_zero] / window_fix[w_non_zero]
return y
вычислить игрушечный пример
w_length = 400 # 20ms for 16kHz signal
w_step = 240 # 15ms for 16kHz signal - 10ms overlaped, standart for speech processig
window = np.hamming
y = 1 + np.random.randn(16000)
s = stft(y, w_length=w_length, w_shift=w_step, window=window)
y_recovery = istft(s, w_length=w_length, w_shift=w_step, window=window)
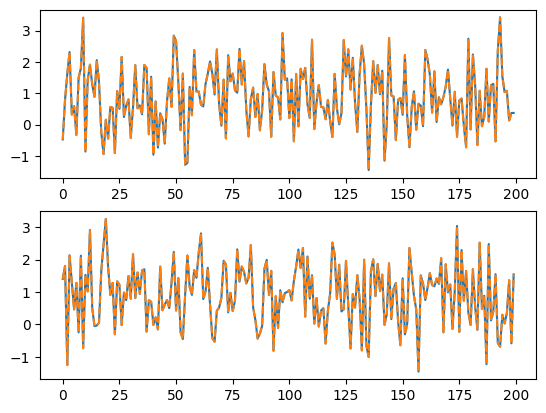
проверить результат на краю окна
plt.subplot(2,1,1)
plt.plot(y[350:550])
plt.plot(y_recovery[350:550], '--')
plt.subplot(2,1,2)
plt.plot(y[0:200])
plt.plot(y_recovery[0:200], '--')
Я думаю, что у scipy.signal есть то, что вы ищете. Он имеет разумные значения по умолчанию, поддерживает несколько типов окон и т.д...
http://docs.scipy.org/doc/scipy-0.17.0/reference/generated/scipy.signal.spectrogram.html
from scipy.signal import spectrogram
freq, time, Spec = spectrogram(signal)
Если у вас есть доступ к двоичной библиотеке C, которая делает то, что вы хотите, то используйте http://code.google.com/p/ctypesgen/ для создания интерфейса Python для этой библиотеки.