Эмуляция Excel сплит-функции "сплит с гладкой кривой" в Matplotlib для 3 точек
Я пытаюсь подражать Excel
Вставка>Scatter>Scatter с плавными линиями и маркерами
Команда в Матплотлибе
Функция scipy interpolate создает аналогичный эффект, с некоторыми хорошими примерами того, как просто реализовать это здесь: Как нарисовать кубический сплайн в matplotlib
Однако сплайн-алгоритм Excel также способен генерировать плавную кривую всего за три точки (например, x = [0,1,2] y = [4,2,1]); и это невозможно сделать с кубическими сплайнами.
Я видел обсуждения, которые предполагают, что алгоритм Excel использует сплайны Катмулла-Рома; но на самом деле не понимаю их, или как их можно адаптировать к Matplotlib: http://answers.microsoft.com/en-us/office/forum/office_2007-excel/how-does-excel-plot-smooth-curves/c751e8ff-9f99-4ac7-a74a-fba41ac80300
Существует ли простой способ изменения приведенных выше примеров для получения плавных кривых через три или более точек с использованием библиотеки интерполяции?
Большое спасибо
2 ответа
К настоящему времени вы, возможно, нашли страницу Википедии для центростремительного сплайна Catmull-Rom, но, если вы этого не сделали, она включает следующий пример кода:
import numpy
import matplotlib.pyplot as plt
def CatmullRomSpline(P0, P1, P2, P3, nPoints=100):
"""
P0, P1, P2, and P3 should be (x,y) point pairs that define the
Catmull-Rom spline.
nPoints is the number of points to include in this curve segment.
"""
# Convert the points to numpy so that we can do array multiplication
P0, P1, P2, P3 = map(numpy.array, [P0, P1, P2, P3])
# Calculate t0 to t4
alpha = 0.5
def tj(ti, Pi, Pj):
xi, yi = Pi
xj, yj = Pj
return ( ( (xj-xi)**2 + (yj-yi)**2 )**0.5 )**alpha + ti
t0 = 0
t1 = tj(t0, P0, P1)
t2 = tj(t1, P1, P2)
t3 = tj(t2, P2, P3)
# Only calculate points between P1 and P2
t = numpy.linspace(t1,t2,nPoints)
# Reshape so that we can multiply by the points P0 to P3
# and get a point for each value of t.
t = t.reshape(len(t),1)
A1 = (t1-t)/(t1-t0)*P0 + (t-t0)/(t1-t0)*P1
A2 = (t2-t)/(t2-t1)*P1 + (t-t1)/(t2-t1)*P2
A3 = (t3-t)/(t3-t2)*P2 + (t-t2)/(t3-t2)*P3
B1 = (t2-t)/(t2-t0)*A1 + (t-t0)/(t2-t0)*A2
B2 = (t3-t)/(t3-t1)*A2 + (t-t1)/(t3-t1)*A3
C = (t2-t)/(t2-t1)*B1 + (t-t1)/(t2-t1)*B2
return C
def CatmullRomChain(P):
"""
Calculate Catmull Rom for a chain of points and return the combined curve.
"""
sz = len(P)
# The curve C will contain an array of (x,y) points.
C = []
for i in range(sz-3):
c = CatmullRomSpline(P[i], P[i+1], P[i+2], P[i+3])
C.extend(c)
return C
который хорошо вычисляет интерполяцию для n >= 4 баллы как то так:
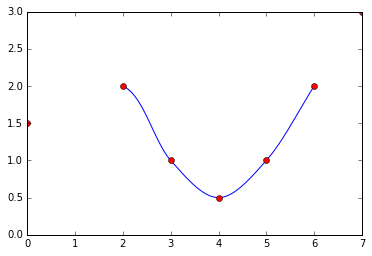
points = [[0,1.5],[2,2],[3,1],[4,0.5],[5,1],[6,2],[7,3]]
c = CatmullRomChain(points)
px, py = zip(*points)
x, y = zip(*c)
plt.plot(x, y)
plt.plot(px, py, 'or')
в результате чего matplotlib образ:
Обновить:
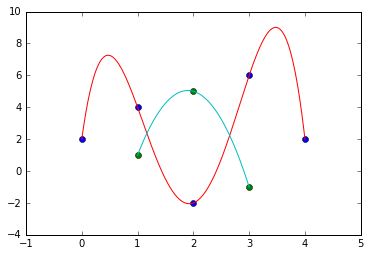
В качестве альтернативы, есть scipy.interpolate функция для BarycentricInterpolator кажется, делает то, что вы ищете. Это довольно просто для использования и работает для случаев, когда у вас есть только 3 точки данных.
from scipy.interpolate import BarycentricInterpolator
# create some data points
points1 = [[0, 2], [1, 4], [2, -2], [3, 6], [4, 2]]
points2 = [[1, 1], [2, 5], [3, -1]]
# put data into x, y tuples
x1, y1 =zip(*points1)
x2, y2 = zip(*points2)
# create the interpolator
bci1 = BarycentricInterpolator(x1, y1)
bci2 = BarycentricInterpolator(x2, y2)
# define dense x-axis for interpolating over
x1_new = np.linspace(min(x1), max(x1), 1000)
x2_new = np.linspace(min(x2), max(x2), 1000)
# plot it all
plt.plot(x1, y1, 'o')
plt.plot(x2, y2, 'o')
plt.plot(x1_new, bci1(x1_new))
plt.plot(x2_new, bci2(x2_new))
plt.xlim(-1, 5)
Обновление 2
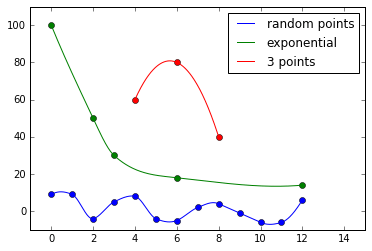
Другой вариант в scipy это интерполяция Акимы через Akima1DInterpolator, Он так же прост в реализации, как и Barycentric, но имеет то преимущество, что он позволяет избежать больших колебаний на границе набора данных. Вот несколько тестов, которые показывают все критерии, которые вы запрашивали до сих пор.
from scipy.interpolate import Akima1DInterpolator
x1, y1 = np.arange(13), np.random.randint(-10, 10, 13)
x2, y2 = [0,2,3,6,12], [100,50,30,18,14]
x3, y3 = [4, 6, 8], [60, 80, 40]
akima1 = Akima1DInterpolator(x1, y1)
akima2 = Akima1DInterpolator(x2, y2)
akima3 = Akima1DInterpolator(x3, y3)
x1_new = np.linspace(min(x1), max(x1), 1000)
x2_new = np.linspace(min(x2), max(x2), 1000)
x3_new = np.linspace(min(x3), max(x3), 1000)
plt.plot(x1, y1, 'bo')
plt.plot(x2, y2, 'go')
plt.plot(x3, y3, 'ro')
plt.plot(x1_new, akima1(x1_new), 'b', label='random points')
plt.plot(x2_new, akima2(x2_new), 'g', label='exponential')
plt.plot(x3_new, akima3(x3_new), 'r', label='3 points')
plt.xlim(-1, 15)
plt.ylim(-10, 110)
plt.legend(loc='best')
@Lanery: Re: Обновление 2: лучшее стало еще лучше!
Пришлось переопределить списки x2,y2,x3,y3 как массивы, чтобы ваш пример работал на моей системе (Spyder / Python 2.7):
x2 = np.array([0,2,3,6,12])
y2 = np.array([100,50,30,18,14])
x3 = np.array([4, 6, 8])
y3 = np.array([60, 80, 40])
Но сейчас работает как мечта! Большое спасибо за ваш опыт и четкие объяснения.