Неоднозначность при переходе: как обработать строку в NFA?
Я сделал DFA из данного регулярного выражения, чтобы соответствовать тестовой строке. Есть несколько случаев, когда .* происходит. (например .*ab) Допустим, сейчас машина находится в состоянии 1. В ДФА, .* относится к переходу для всех символов к себе и другому переходу для a из состояния 1 для 'a'. Если тестовая строка содержит "a", то каким может быть переход, потому что из состояния 1 машина может перейти в два состояния, что невозможно в DFA.
2 ответа
Я начну с фундаментального с вашего примера, чтобы можно было найти его полезным
Любой класс автоматов может иметь две формы:
- детерминистический
- Недетерминированные.
В детерминированной модели: у нас есть только один выбор (или, скажем, нет выбора), чтобы перейти от одного поздравления к следующей конфигурации.
В Детерминированной модели Finite Automate (DFA): для каждой возможной комбинации состояния (Q) и символа языка (Σ) у нас всегда есть уникальное следующее состояние.
Определение функции перехода для DFA: δ:Q×Σ → Q
δ(q0, a) → q1
^ only single choice
Таким образом, в DFA каждый возможный шаг определен из одного состояния в другое.
В то время как,
В недетерминированной модели: у нас может быть несколько вариантов для следующей конфигурации.
А в недетерминированной модели конечных автоматов (NFA): выходные данные представляют собой набор состояний для некоторой комбинации состояния (Q) и символа языка (Σ).
Определение функции перехода для NFA: δ: Q × Σ → 2 Q = ⊆ Q
δ(q0, a) → {q1, q2, q3}
^ is set, Not single state (more than one choice)
В NFA у нас может быть более одного выбора для следующего штата. То есть вы называете двусмысленность в переходе NFA.
(твой пример)
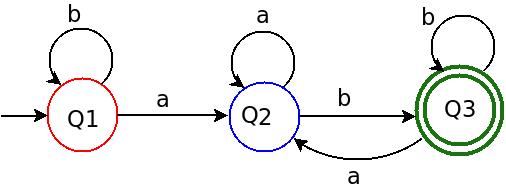
Предположим, языковые символы Σ = {a, b} и язык / регулярное выражение (a + b)*ab, Конечные автоматы для этого языка, который вы используете, могут быть, как показано ниже:
Ваш вопрос:Which state to move when we have more than one choices for next state?
Я делаю это более общим вопросом.
Как обработать строку в NFA?
Я рассматриваю модель автомата в качестве акцептора, который принимает строку, если она принадлежит языку автоматов (обратите внимание: у нас может быть автомат в качестве преобразователя), ниже приведен мой ответ с приведенным выше примером.
В вышеупомянутом NFA мы находим 5 тапулярных объектов:
1. Σ : {a, b}
2. Q : {q1, ,q2, q3}
3. q1: initial state
4. F : {q3} <---F is set of final state
5. δ : Transition rules in above diagram:
δ(q1, a) → { q1, q2 }
δ(q1, b) → { q1 }
δ(q2, b) → { q3 }
Предполагаемые конечные автоматы являются фактически NFA, потому что в производственном правиле δ(q1, a) → { q1, q2 } если мы получим a символ в то время как настоящее состояние q1 тогда следующие состояния могут быть q1 или же q2 (более одного варианта). Поэтому, когда мы обрабатываем строку в NFA, мы получаем дополнительный путь для перемещения туда, где их символ a быть процесс, пока текущее состояние q1,
NFA принимает строку, если существует некоторая последовательность возможных ходов, которая переводит машину в конечное состояние в конце обработки строки. И множество всех строк, которые имеют некоторый путь для достижения любого конечного состояния в наборе F Из исходного состояния называется язык NFA:
Мы также можем написать "что такое язык, определенный NFA?" как:
L(nfa) = {w ⊆ Σ* | δ * (q 1, w) ∩ F ≠ ∅}
когда я был новым, это было слишком сложно, чтобы понять для меня, но на самом деле это не так
L(nfa) говорит: все строки состоят из символов языка = (w ⊆ Σ*) на языке; если (|) множество состояний получают после обработки w Начальное состояние формы (=δ*(q1, w)) содержит несколько состояний из множества конечных состояний (следовательно, пересечение с конечными состояниями не пусто = δ*(q1, w) ∩ F ≠ ∅). Таким образом, при обработке строки в Σ* нам необходимо отслеживать все возможные пути.
Пример-1: обработать строку abab хотя выше NFS:
--►(q1)---a---►(q1)---b---►(q1)---a---►(q1)---b---►(q1)
\ \
a a
\ \
▼ ▼
(q2) (q2)---b---►((q3))
|
b
|
▼
(q3)
|
a
|
halt
Над диаграммой показано: как обработать строку abab в нфу?
Остановка: означает, что строка не может быть полностью обработана, поэтому ее нельзя считать принятой строкой в этом пути.
строка abab может полностью обрабатываться в двух направлениях, поэтому δ*(q1, w) = { q1, q3}.
и пересечение δ * (q1, w) с множеством конечных состояний равно {q3}:
{q1, q3} ∩ F
==> {q1, q3} ∩ {q3}
==> {q3} ≠ ∅
Таким образом, строка ababa находится на языке L (нфа).
Пример 2: строка из Σ* is abba и вот как это обрабатывать:
--►(q1)---a---►(q1)---b---►(q1)---b---►(q1)---a---►(q1)
\ \
a a
\ \
▼ ▼
(q2) (q2)
|
b
|
▼
(q3)
|
b
|
halt
Для строки abba множество достижимых состояний: δ*(q1, w) = { q1, q2} и ни одно из состояний не является конечным состоянием в этом наборе, это подразумевает => его пересечение с F является ∅ пустым множеством, поэтому строка abba не является принятой строкой (и не на языке).
Это способ обработки строки в недетерминированных конечных автоматах.
Некоторые дополнительные важные замечания:
В случае конечных автоматов как детерминированные, так и недетерминированные модели одинаково способны. Недетерминированная модель не имеет дополнительной возможности определять язык. следовательно, область действия NFA и DFA такая же, как и у Regular Language. (это не относится ко всем классам автоматов, например, область применения КПК! = NPDA)
Недетерминированные модели более полезны для теоретических целей, для сравнения - эссе для рисования. Принимая во внимание, что для целей реализации мы всегда хотим детерминистическую модель (минимизированную для эффективности). И, к счастью, в классе конечных автоматов каждая недетерминированная модель может быть преобразована в эквивалентную детерминистскую. У нас есть алгоритмический метод для преобразования NFA в DFA.
Информация, представленная одним состоянием в DFA, может быть представлена комбинацией состояний NFA, следовательно, число состояний в NFA меньше, чем их эквивалентный DFA. (доказательство доступно: numberOfStates(DFA)<= 2 power numberOfStates(NFA), так как все заданные комбинации являются powerset)
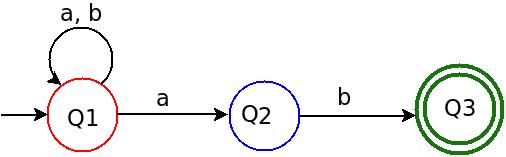
DFA для вышеуказанного обычного языка, как показано ниже:
Используя этот DFA, вы всегда найдете уникальный путь от начального состояния до конечного состояния для любой строки в Σ*, и вместо набора вы попадете в единственное достижимое конечное состояние, и если это состояние принадлежит множеству финальных элементов, о котором говорят, что входная строка принимается строка (на языке) в противном случае не /
(ваше выражение .*ab а также (a + b)*ab такие же, как правило, в теоретической науке мы не используем . оператор точки, кроме конкатенации)
Совпадения с такими регулярными выражениями происходят через возврат. Когда возникает неопределенность в отношении следующего состояния, оценка выбирает первый выбор и запоминает, что он сделал выбор. Если выбор первого варианта приводит к несоответствию, оценка возвращается к последнему выбранному варианту и пробует следующий доступный выбор из этого состояния.
Я не уверен, что такой механизм соответствует строгому DFA.