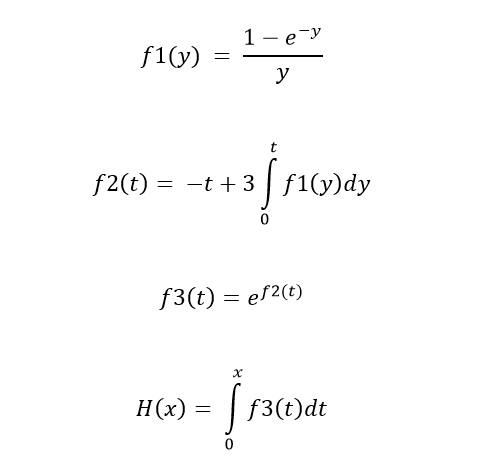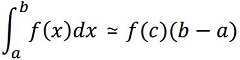Как выполнить неопределенную интеграцию этой функции в MATLAB?

Question

Мне нужно выполнить следующие операции, как показано на рисунке. Мне нужно рассчитать значение функции H для разных входов (х), используя MATLAB.

Я даю следующую команду из Symbolic Math Toolbox

syms y t x;
f1=(1-exp(-y))/y;
f2=-t+3*int(f1,[0,t]);
f3=exp(f2);
H=int(f3,[0,x]);

но значение 2-го интеграла, т. е. интеграла в функцию H, не может быть вычислено, и мой вывод имеет вид

H =

int(exp(3*eulergamma - t - 3*ei(-t) + 3*log(t)), t, 0, x)

Если кто-то из вас, ребята, знает, как оценить это или имеет другое представление об этом, пожалуйста, поделитесь им со мной.

Answer 1

Непосредственный поиск численного решения с использованием integral:

Так как вы хотите рассчитать H для разных значений x Таким образом, вместо аналитического решения, вы можете перейти к численному решению.

Код:

syms y t;
f1=(1-exp(-y))/y;   f2=-t+3*int(f1,[0,t]);  f3=exp(f2);
H=integral(matlabFunction(f3),0,100)   % Result of integration when x=100 

Выход:

H =
   37.9044

---

Поиск приближенного аналитического решения с использованием интеграции Монте-Карло:

Вероятно, это " эллиптический интеграл ", и его нельзя выразить через элементарные функции. Тем не менее, вы можете найти приблизительное аналитическое решение, используя " Интеграция Монте-Карло ", согласно которому:

где f (c) = ¹ / _n Σf (xᵢ)

Код:

syms x y t;

f1=(1-exp(-y))/y;   f2=-t+3*int(f1,[0,t]);  f3=exp(f2);
f3a= matlabFunction(f3);       % Converting to function handle

n = 1000;      
t = x*rand(n,1);               % Generating random numbers within the limits (0,x)
MCint(x) = x * mean(f3a(t));   % Integration
H= double(MCint(100))          % Result of integration when x=100  

Выход:

H =
   35.2900

% Output will be different each time you execute it since it is based
% on generation of random numbers

Недостатки этого подхода:

1. Решение не точное, но приблизительное.
2. Большее значение n, лучше результат и медленнее скорость выполнения кода.

---

^{Прочитайте документацию} matlabFunction ^, integral ^{Случайные числа в определенном диапазоне,} mean ^{а также} double ^{для дальнейшего понимания кода (ов).}