Планирование пути для нескольких роботов одновременно

Question

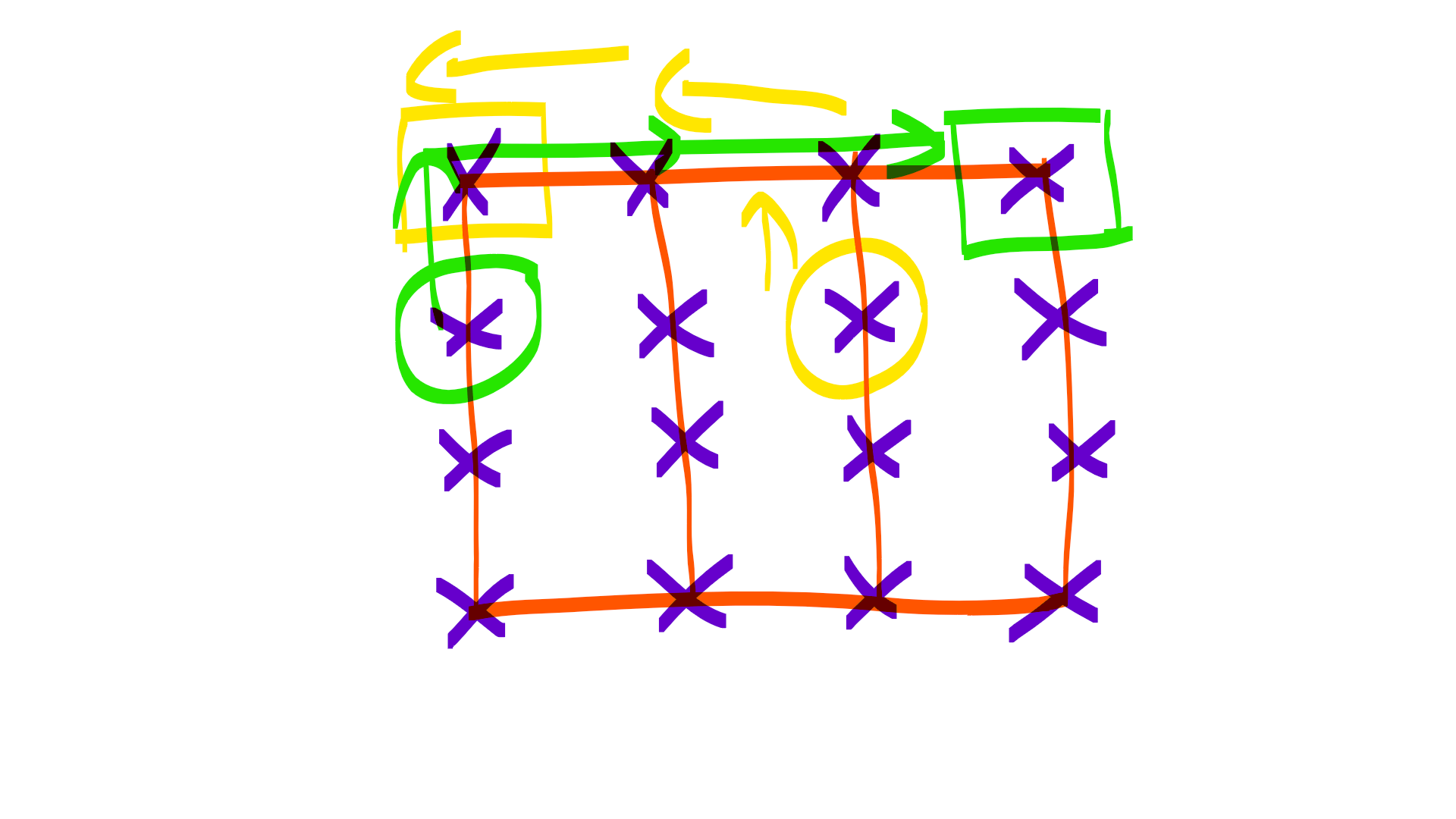
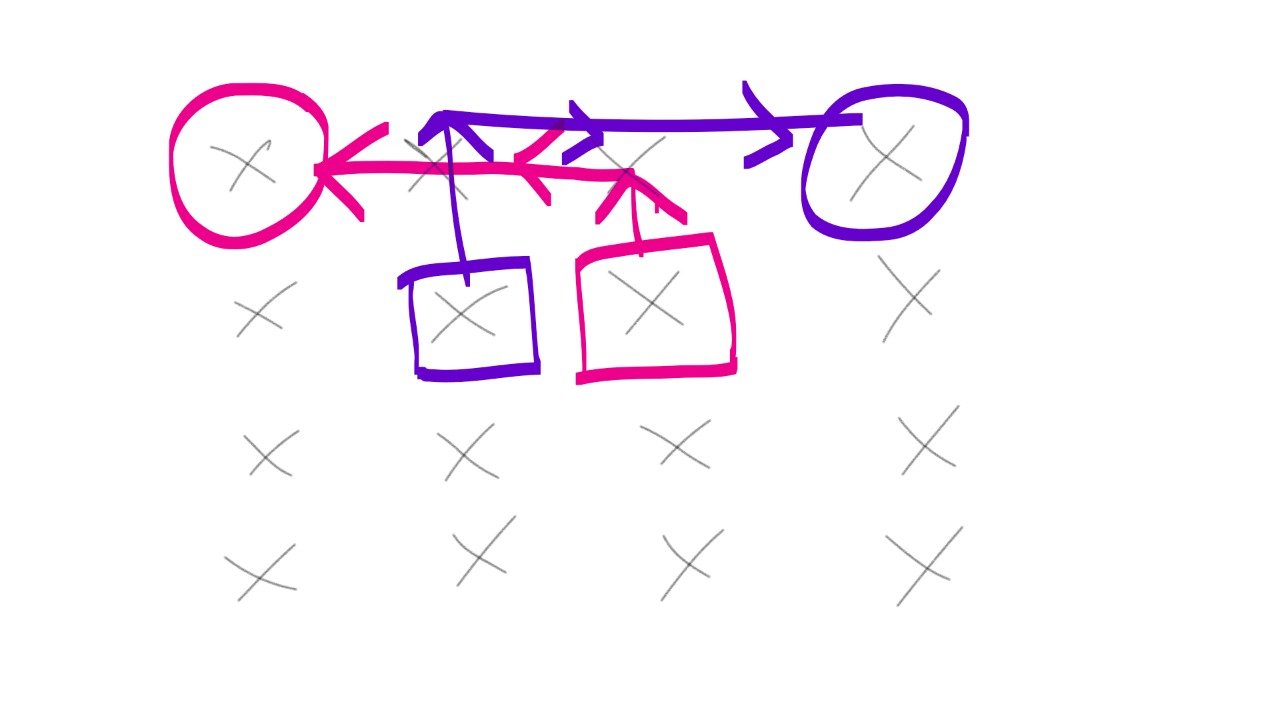
Изображение 1 отлично отражает проблему и показывает свободу движений, на которую способен робот.

Квадрат-> Источник, Круг-> Пункт назначения.

Это два робота, которые будут работать одновременно. Как вести этих роботов, не блокируя друг друга, и если кто-то из них должен двигаться первым, то как выбрать, какой из них.

(приведенный выше случай является лишь примером, я знаю, что в этом случае мы можем произвольно остановить любого из них и избежать неприятностей с этим, но я ищу обобщенное решение. Подход к ближайшему соседу запрещен.)ПРИМЕЧАНИЕ: робот не может двигаться поперек, за исключением верхнего и нижнего рядов.

У меня есть все точки, отмеченные X, а также маршруты для них в идентификаторах и координатах ниже,

# X generated points  
{1: [0, 0], 2: [0, 30], 3: [0, 60], 4: [0, 90], 5: [30, 0], 6: [30, 30], 7: [30, 60], 8: [30, 90], 9: [60, 0], 10: [60, 30], 11: [60, 60], 12: [60, 90], 13: [90, 0], 14: [90, 30], 15: [90, 60], 16: [90, 90]}

# Routes:
red=[11,12,8,4]
blue=[7,8,12,6]

Answer 1

Делать градиентный спуск в потенциальном поле.

Думайте о вашей доске как о 3-х мерной (хорошо, 2,5-мерной), с "горами", где барьеры, такие как стены, и "долиной", где цель. Каждый робот поддерживает свое собственное потенциальное поле, которое может иметь такое же или более высокое разрешение, чем нарисованная вами сетка. Поля могут меняться как функция времени t,

Итак, теперь у вас есть функция, z(x, y, t)что вы можете исследовать непосредственное соседство робота, на котором вы можете вычислить дельты (градиенты), показывающие вам путь "вниз", путь к целевому состоянию. Например, при прохождении по коридору ваш робот предпочитает идти по центру, потому что потенциальные поля будут выходить за пределы стен, по существу отталкивая робота. Сетка, которую вы нарисовали, окружена 4 непроходимыми стенами.

Теперь давайте перейдем от фиксированных препятствий к мобильным одноранговым роботам. Похоже, у вас есть какие-то средства, чтобы робот мог передать свои намерения своим сверстникам. У робота есть планировщик A*, который предсказывает, что он будет посещать определенные места в определенное время в будущем. Конечно, это может не сработать из-за шумов датчиков и неопределенности событий, но это план. Так что передавайте это пэрам. Они добавят ожидаемый путь к потенциальному полю, которое они используют, поэтому другие роботы создают отталкивающее поле, как стены и неподвижные объекты. Это побуждает сверстника планировать траекторию движения вокруг препятствия (робота), который, как ожидается, будет в будущем. Можно по-прежнему сталкиваться с локальными максимумами и взаимными блокировками, поэтому все равно потребуется некоторое количество случайного отката. Например, два робота, встречающиеся лицом к лицу в зале, с некоторым случайным шумом, мы надеемся, выберут одну сторону или другую, но не определено, будут ли это лондонские или манхэттенские правила вождения, левая или правая сторона.

Такая техника, как заливка, может распространять градиентные стимулы наружу от цели, чтобы побудить робота отойти "от цели", чтобы обойти лабиринтные барьеры.

Этот подход работает для автономных роботов со спорадическим зондированием / связью, а также для роботов с централизованным управлением. Центральный контроллер будет поддерживать один план на робота, а также одно потенциальное поле на робота, соответствующее препятствиям и сверстникам. Траектории от начала до конца могут быть собраны компонентом Planner еще до того, как первая команда движения была отправлена ​​физическому роботу. Если планировщик проходит через роботов 1..N, роботы с меньшим номером будут стремиться к более коротким путям, поскольку они сначала объявляют планы и пользуются большей свободой передвижения. Например, если Пурпур движется первым в момент времени t0, то его потенциальное поле по существу сливается с полем стены в течение времени t1 и последующего, поэтому Пинк естественным образом строит планы, которые избегают стены, и, следовательно, оба остаются конфликтующими. Вы можете думать об этом как о фиолетовом, имеющем приоритет над розовым.

Answer 2

Если ваш лабиринт / сетка имеет много вариантов для перехода от источника к цели, будет работать следующий "жадный" алгоритм:

• Используйте алгоритм кратчайшего пути, чтобы построить путь для первого робота.
• Удалить все вершины найденного пути из лабиринта
• Повторите для следующего робота (ов)

Это разрешает маршруты по одному роботу за раз. Удаляя путь (и) предыдущего робота (ов) из лабиринта, вы не позволяете другому роботу (ам) использовать тот же путь.

Существует вероятность того, что два робота попытаются занять один и тот же узел, но это не приведет к их взаимной блокировке, поскольку их пути входа и выхода уникальны. Один из двух роботов должен будет просто подождать один ход, пока другой не исчезнет. Просто позвольте роботу [i] получить приоритет над роботом [j] для меня

Answer 3

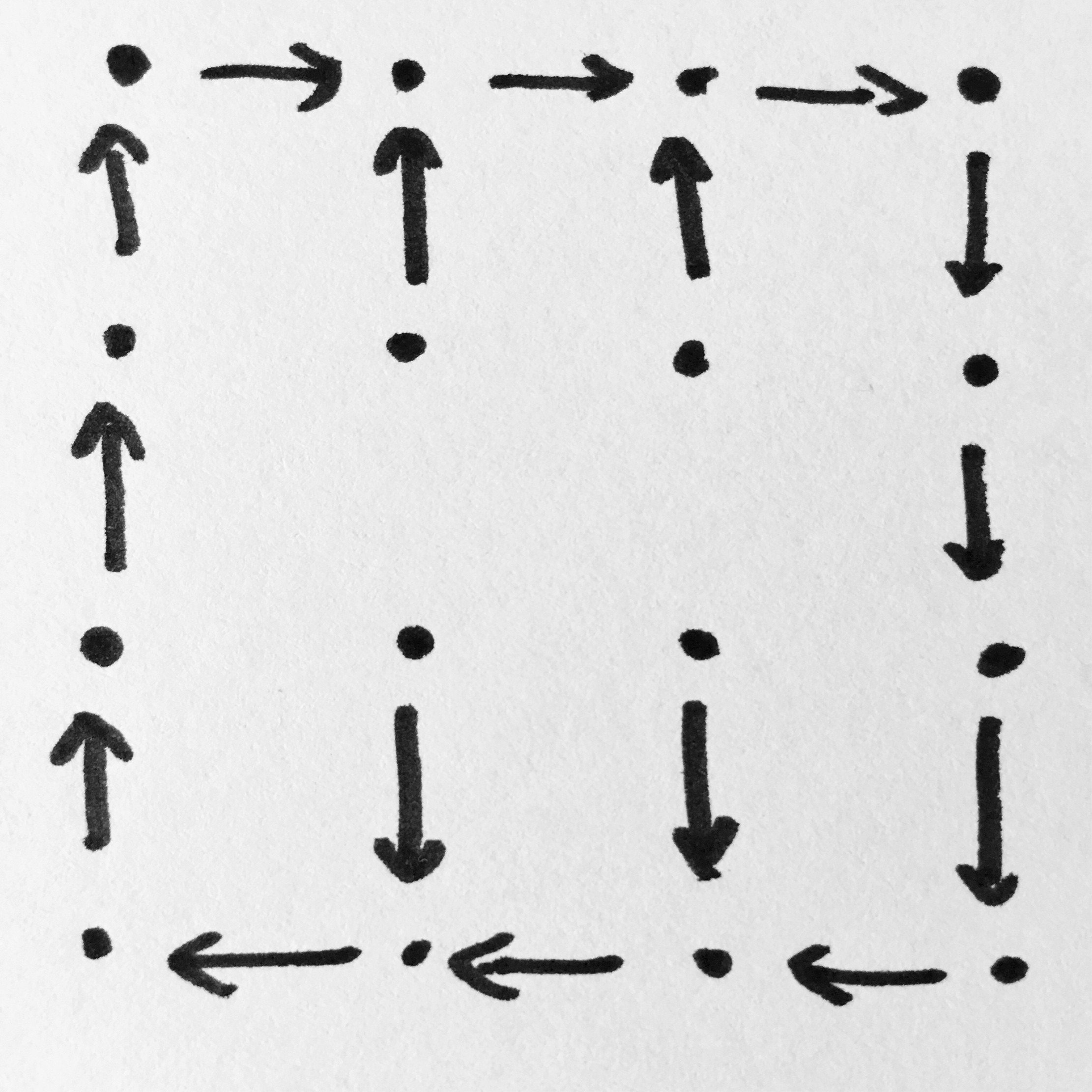
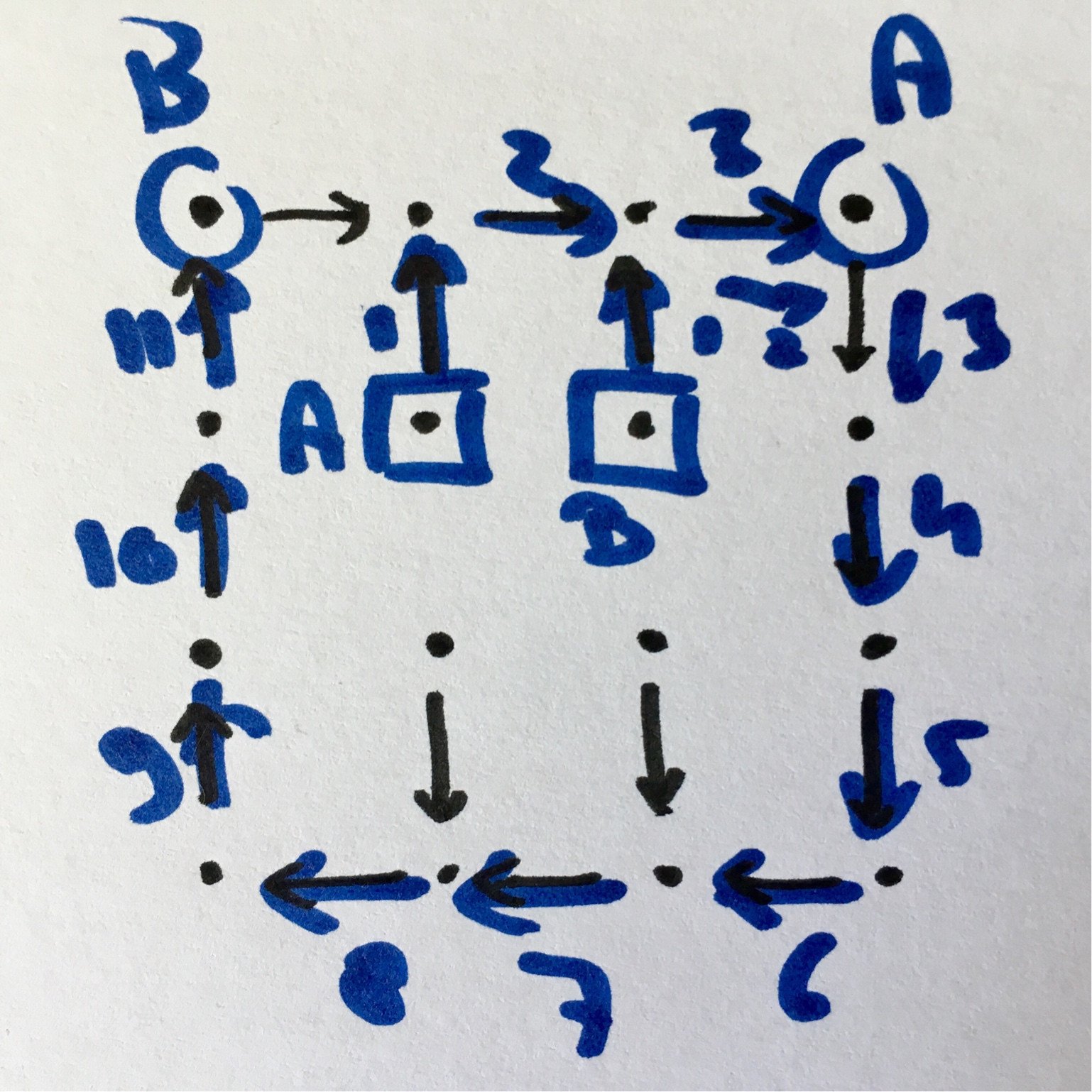
Пусть все роботы поворачиваются по внешнему кругу, пока пункт назначения не будет на расстоянии одного шага, и пункт назначения не станет пустым. В этом случае перейдите к пункту назначения.

Таким образом, алгоритм становится:

• если внутренний круг и внешний круг свободны, двигайтесь туда; иначе подождите один цикл (или, если это не разрешено, сделайте шаг во внутреннем круге)
• если во внешнем круге, проверьте, находится ли пункт назначения на расстоянии 1 шага. Если это так, иди туда. В противном случае сделайте один шаг по внешнему кругу.

Нет столкновений. Никаких странных случаев. Работает 100% времени.

Применительно к вашему примеру: робот А вернется домой за 3 шага. Робот Б сделает 11 шагов.