Теорема об интегральности в максимальном потоке

Question

Теорема об интегральности говорит нам, что если все емкости в сети потока являются целыми числами, то существует максимальный поток, где каждое значение является целым числом

Но самая замечательная часть - это существование, а не каждый максимальный поток! Это означает, что это утверждение не утверждает, что каждый максимальный поток является целочисленным

Я не могу понять, почему, если все емкости целочисленные, но существует максимальный поток, не целочисленный!!

Или я просто неправильно понял эту теорему, которая пытается мне сказать?

Answer 1

Позволять

• е = ребро на графике.
• c (e) = емкость данного ребра e
• f (e) = количество потока, проходящего через заданное ребро e

Теорема утверждает:

Если c (e) для всех ребер, e в графе являются целыми числами, то существует максимальный поток f, для которого каждое значение потока f (e) является целым числом.

Обратите внимание, что теорема не накладывает ограничения на f (e).

Только c (e) должно быть целым числом.
Поскольку "c(e) должно быть целым числом", это также не означает, что "f(e) должно быть целым числом".
Поэтому вполне допустимо иметь нецелочисленный поток с целочисленной емкостью.

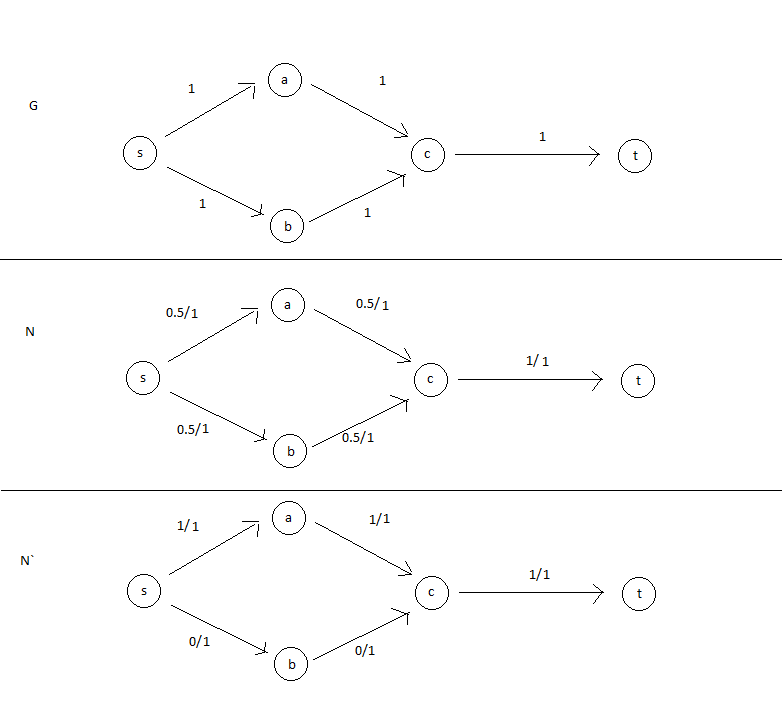
Вот пример, где все емкости являются целочисленными с максимальным потоком, у которого есть некоторые ребра, которые имеют нецелочисленный поток.

G - граф потока, с которым я работаю.. N - максимальный интегральный поток.. N` - максимальный поток, в котором у некоторых ребер есть нецелочисленный поток..

номер пары по краям имеет формат: "поток / емкость"

Помните, что теорема говорит только о том, что верхняя граница функции f(u,v) является целым числом... она ничего не говорит о ее нижней границе... поэтому поток может быть любым числом от 0 до c(u,v)..

Answer 2

Если для получения максимального потока используется метод Форда-Фулкерсона, то полученный поток должен быть целочисленным

Но у нас все еще может быть максимальный поток, который использует действительное число в качестве значения потока по краям

Проверьте этот пример:

          B
        /   \
       /     \
      /       \

Суббота

      \       /
       \     /
        \   /
          C

направления ребер все идут слева направо, и (s,a) имеет 1 поток и 1 емкость,

а в остальном все идут с 0,5 потока и 1 вместимостью.

Это потоковая сеть, имеющая максимальный поток, но не целочисленная.