Не удается заставить уравнения Лотки-Вольтерра колебаться стабильно с помощью math.js

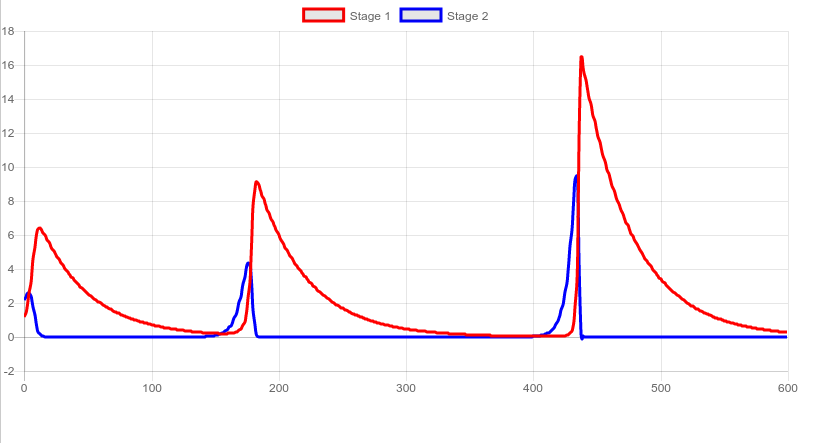
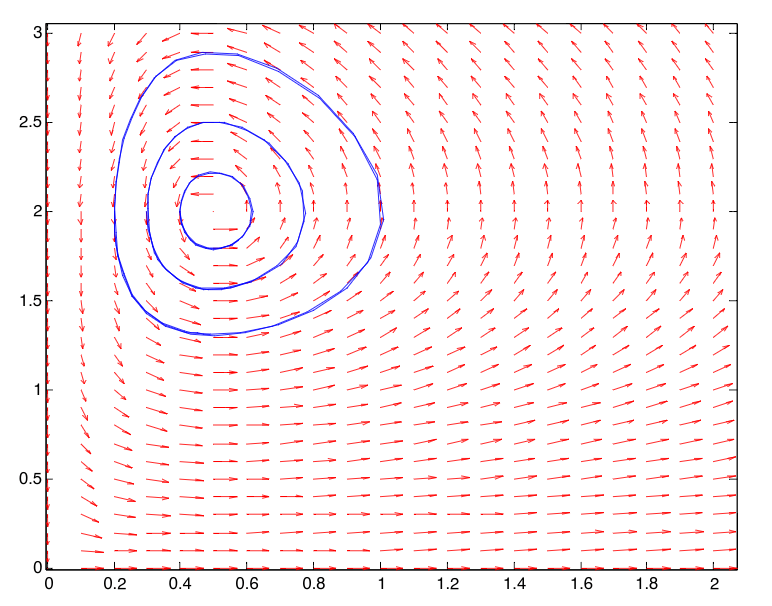
Я пытаюсь реализовать простую систему Лотка-Вольтерра в JavaScript, но получаю результат, отличный от того, что я вижу в научных статьях и слайдах. Это мои уравнения:

sim2.eval("dxdt(x, y) = (2 * x) - (x * y)");
sim2.eval("dydt(x, y) = (-0.25 * y) + (x * y)");

используя коэффициенты a = 2, b = 1, c = 0.25 и d = 1. Тем не менее, мой результат выглядит так:

когда я ожидал стабильных колебаний, как видно на этих слайдах PDF:

Может ли это быть причиной реализации ndsolve? Или машинная ошибка в JavaScript из-за арифметики с плавающей точкой?

Источник

2 ответа

Решение

Для серьезных целей используйте метод более высокого порядка, минимальный фиксированный шаг - классический Рунге-Кутта. Тогда вы также можете использовать dt=0.1, стабильно в течение нескольких периодов, я пытался tfinal=300 без проблем. Однако вы увидите размер шага на графике, так как он визуально кусочно-линейный. Это значительно уменьшается с половиной размера шага, dt=0.05,

function odesolveRK4(f, x0, dt, tmax) {
  var n = f.size()[0];  // Number of variables
  var x = x0.clone(),xh=[];   // Current values of variables
  var dxdt = [], k1=[], k2=[], k3=[], k4=[];        // Temporary variable to hold time-derivatives
  var result = [];      // Contains entire solution

  var nsteps = math.divide(tmax, dt);   // Number of time steps
  dt2 = math.divide(dt,2);
  dt6 = math.divide(dt,6);
  for(var i=0; i<nsteps; i++) {
    // compute the 4 stages if the classical order-4 Runge-Kutta method
    k1 = f.map(function(fj) {return fj.apply(null, x.toArray()); } );
    xh = math.add(x, math.multiply(k1, dt2));
    k2 = f.map(function(fj) {return fj.apply(null, xh.toArray()); } ); 
    xh = math.add(x, math.multiply(k2, dt2));
    k3 = f.map(function(fj) {return fj.apply(null, xh.toArray()); } ); 
    xh = math.add(x, math.multiply(k3, dt));
    k4 = f.map(function(fj) {return fj.apply(null, xh.toArray()); } ); 
    x = math.add(x, math.multiply(math.add(math.add(k1,k4), math.multiply(math.add(k2,k3),2)), dt6))

    if( 0==i%50) console.log("%3d %o %o",i,dt,x.toString());
    result.push(x.clone());
  }

  return math.matrix(result);
}

math.import({odesolveRK4:odesolveRK4});
Источник

Не обращайте внимания, ошибка заключалась в использовании слишком большого шага оценки (dt = 0,1, должно быть не менее 0,01). Используемый численный метод известен для этой проблемы.

Источник
Другие вопросы по тегам