Объединение Пересекающихся CGPaths на iOS
У меня проблема в приложении, над которым я работаю. Скажем, у меня есть два довольно сложных CGPath, и я добавляю их обоих в CGMutablePath (таким образом, объединяя их). Что ж, там, где пересекаются два пути, будут точки внутри друг друга. Я хочу устранить эти внутренние точки и по существу нарисовать внешнюю или контурную схему пути. Мне трудно понять, как я поступил бы по этому поводу.
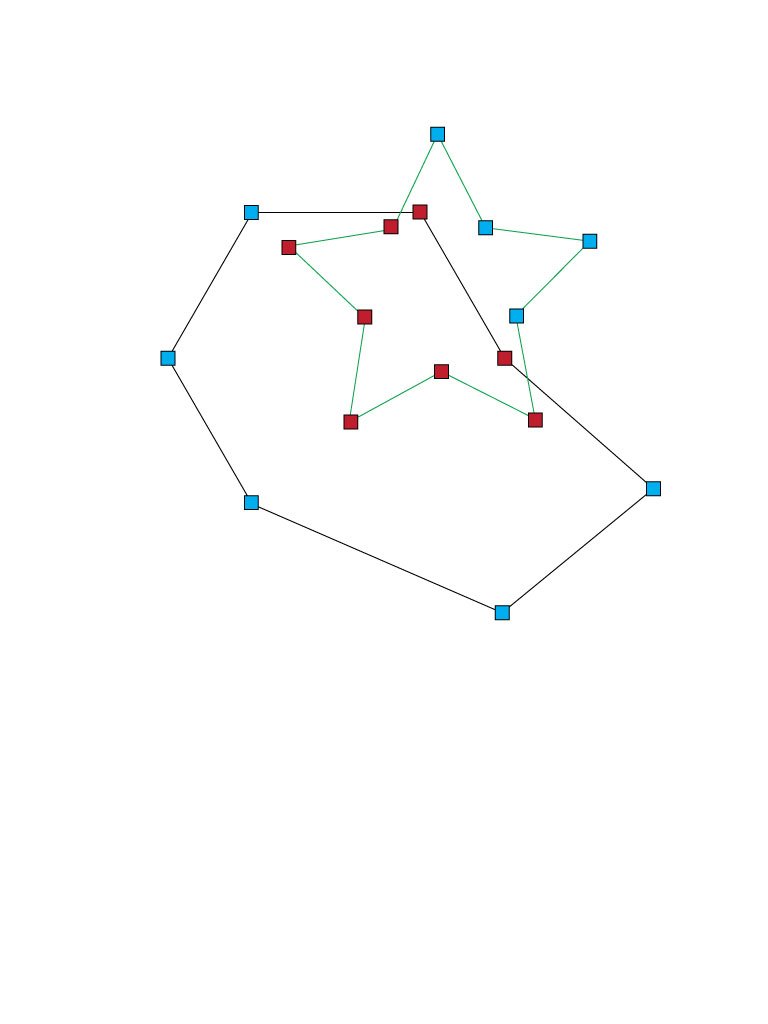
Изменить: вот пример того, о чем я говорю. Синие и красные прямоугольники представляют точки вдоль CGPaths. Красные прямоугольники - это точки, которые находятся внутри обоих путей. Я хотел бы как-то устранить красные точки и перерисовать только контур пути.
4 ответа
То, что вы описываете, - это объединение внутренностей путей.
Если ваши пути содержат кривые, это сложная проблема.
Однако в вашем примере показаны только отрезки прямых линий, поэтому я предполагаю, что вы заботитесь только о путях, которые содержат только отрезки прямых линий.
В этом случае вам нужна функция объединения полигонов. Этот вид алгоритма довольно прост в области, известной как "вычислительная геометрия". Я не знаю какой-либо Objective-C-специфичной реализации объединения полигонов. Вы можете найти чистую библиотеку C, но гораздо проще найти библиотеку C++. Вы можете использовать C++, если вы измените расширение файла с .m в .mm, Вот некоторые библиотеки C++, которые могут вычислить объединение полигонов:
- клипер
- GEOS - посмотри
Polygon::Union - CGAL - см. 2D Регуляризованные логические операции над множествами
- увеличить геометрию - см.
union_
Обратите внимание, что во всех случаях вам нужно будет использовать CGPathApply извлечь вершины вашего пути, если у вас их еще нет в другом формате.
Классическая точка в задаче многоугольника. Удалите все точки в каждом многоугольнике, которые возвращают 1, ссылаясь на другой многоугольник:
int pnpoly(int npol, float *xp, float *yp, float x, float y)
{
int i, j, c = 0;
for (i = 0, j = npol-1; i < npol; j = i++) {
if ((((yp[i] <= y) && (y < yp[j])) ||
((yp[j] <= y) && (y < yp[i]))) &&
(x < (xp[j] - xp[i]) * (y - yp[i]) / (yp[j] - yp[i]) + xp[i]))
c = !c;
}
return c;
}
Объедините два пути с удаленными точками.
Псевдокод для всей процедуры:
define starPoly with 10 points
define simplePoly with 7 points
for each point in starPoly
if ( pnpoly( 7, simplePoly.Xs[], simplePoly.Ys[], point.x, point.y ) == 0 )
clipedStarPoly += point;
for each point in simplePoly
if ( pnpoly( 10, starPoly.Xs[], starPoly.Ys[], point.x, point.y ) == 0 )
clipedSimplePoly += point;
for each point in clipedStarPoly
solutionPoly += point;
for each point in clipedSimplePoly
solutionPoly += point;
solutionPoly += solutionPoly.point[0]
Если вы не думаете, что вам придется играть с конечными точками обрезанных полисов, вы можете просто построить решение poly непосредственно из точечных тестов.
Вы можете использовать трассировку лучей для точки в поли-тесте, попробуйте посмотреть на этой странице
Недостаточно просто объединить два набора точек. Чтобы определить комбинированные полигоны, вам нужно сделать следующее. Извините, у меня есть только псевдокод, я только начал смотреть на эту проблему.
Мы будем рассматривать два многоугольника как A и B. Неважно, какой есть какой.
- Перемещайтесь вокруг многоугольника A, ища любую точку, которая НЕ находится внутри многоугольника B.
- Добавьте эту точку к многоугольнику.
- Продолжайте вокруг многоугольника, проверяя и добавляя каждую точку по очереди.
- Когда вы обнаружите точку, которая находится внутри многоугольника B, посмотрите на линию между ней и предыдущей точкой.
- Узнайте, какая линия на многоугольнике B пересекается с этой линией.
- Определите точку пересечения между этими двумя линиями и добавьте ее к многоугольнику.
- Определите, какая из двух точек, которые определяют пересекающуюся линию, принадлежащую многоугольнику B, НЕ находится внутри многоугольника A, и добавьте это к новому многоугольнику.
- Определите, в каком направлении вокруг многоугольника B вам нужно идти, чтобы следующая точка НЕ была точкой на другом конце линии пересечения, и добавьте ее.
- Повторите с 3, за исключением использования многоугольника B вместо многоугольника A
- Продолжайте, пока не достигнете точки, с которой начинали, при необходимости меняя местами полигоны.
Обратите внимание, что это решение приемлемо только для прямых многоугольников. Когда речь идет о более изогнутой траектории, становится намного сложнее вычислить точки пересечения, не говоря уже о сложностях объединения гладких углов с острыми углами или кривых с отрезками прямых линий.