Чтобы применить оконную функцию к распределению Вигнера-Вилле в Matlab

Question

Мы думали здесь, как создать окно перекрытия 64 Хемминга-64.

h = hamming(64);
h2 = hamming(38);
h = conv(h, h2);

Теперь мы думаем о том, как вы можете применить эту оконную функцию к полученным переменным функции распределения Вигнера-Вилле Auger и др. В Tool- Time-Frequency Toolbox. Функция tfrwv.m не имеет параметров для оконной функции.

Итак, у нас есть эти переменные

[B,T,F] = tfrwv(data, 1:length(data), length(data));

Вот один ответ на связанную проблему, но не полностью то же самое. Один говорит, что применяет оконную функцию к результатам

Просто умножьте, точка за точкой

Размеры h равны 101x1, а T и F 5001x1 - двойные. Таким образом, экстраполяция, по-видимому, необходима для вектора окна при умножении на точку.

Еще одно объяснение здесь

Примерно на половине второго блока кода я применяю оконную функцию к буферизованному сигналу. Это фактически векторное умножение оконной функции с каждым буферизованным блоком данных временных рядов. Я просто использую хитрый диагональный матричный трюк, чтобы сделать это эффективно.

Как вы можете применить оконную функцию к переменным B, T и F?

Answer 1

Была одна ошибка и ее симптомы в моем третьем дополнении к ответу lennon310. 4-е расширение ответа Леннона310

я бегу

h = hamming(64);
h2 = hamming(38);
h = conv(h, h2);    
B = 0; T = 0; F = 0;    
data1 = filter(data(1 : 64),1,h); [B,T,F] = tfrwv(data1, 1:length(data1), length(data1));    
for i=1:133
    data1 = filter(data( 1 + i*37 : 64 + i*37 ),1,h); [b,t,f] = tfrwv(data1, 1:length(data1), length(data1));    
    B = [B b']; T = [T t]; F = [F; f];       
end
data1 = filter(data(4959 : 5001),1,h); [b,t,f] = tfrwv(data1, 1:length(data1), length(data1));    
B = [B b']; T = [T t]; F = [F; f];       
T = 49.8899*T;      % dummy constant to get appropriate time interval

и получить такие фотографии

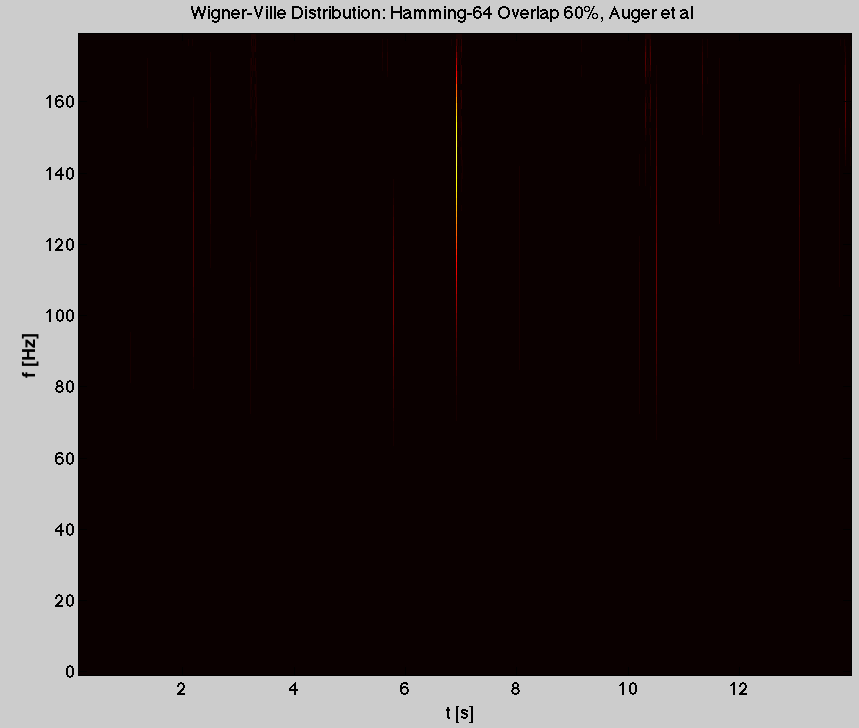
Мне не удалось показать все тонкие пики на одном снимке. Новый вопрос об этом здесь.

Я готовлю это

t = 1/360; % 360 samples per second
fs = 360.5;
imagesc(T*t, F*fs, abs(B))

Алгоритм накапливает точки в нужном измерении.Я не уверен, что умножение на фиктивную константу - верный путь.

Answer 2

Проверьте эту статью о распределении Вигнера. Со страницы 8 до 11. думаю tfr(indices,icol) = x(ti+tau,1) .* conj(x(ti-tau,xcol)); в коде реализуем формулу (23). Сумма и экспоненциальная часть эквивалентны tfr= fft(tfr);, Или вы также можете рассматривать эти две строки кода, которые я привел как формулу (24). Примечание: и в бумаге, и в коде они предполагают, что сигнал является периодическим с N/2, где N является length(data), Это нормально, что вам не нужно менять свой data Вот. Они просто сортируют виды расширения исходных данных.

Цитируется из статьи: Перед обработкой WDF к сигналу временной области применяется модифицированное окно Хемминга, чтобы уменьшить утечку, вызванную прерывистостью конечной записи данных, которая будет называться сужением данных. Насколько я понимаю, что вы можете сделать здесь

data1 = conv(h,data);
[B,T,F] = tfrwv(data1, 1:length(data1), length(data1)); 

Мой ответ сделан на основе вашей реализации. Вы можете попробовать сейчас.

---

Что я не до конца понимаю, так это метод, которым вы создали окно Хэмминга-64 с перекрытием 60%. В spectrogramкод расколол data на небольшие сегменты с длиной каждого 64. Если вы хотите добиться того же эффекта spectrogram с tfrwvЯ думаю, вам также может понадобиться dataи использовать conv(data(1:64),hamming(64)), conv(data(38:101),hamming(64)),conv(data(76:139),hamming(64)).... как вход tfrwv соответственно.

Answer 3

Расширение до ответа lennon310.

я бегу

data1 = conv(h,data);
[B,T,F] = tfrwv(data1, 1:length(data1), length(data1));

а затем построить его с изображением без окон

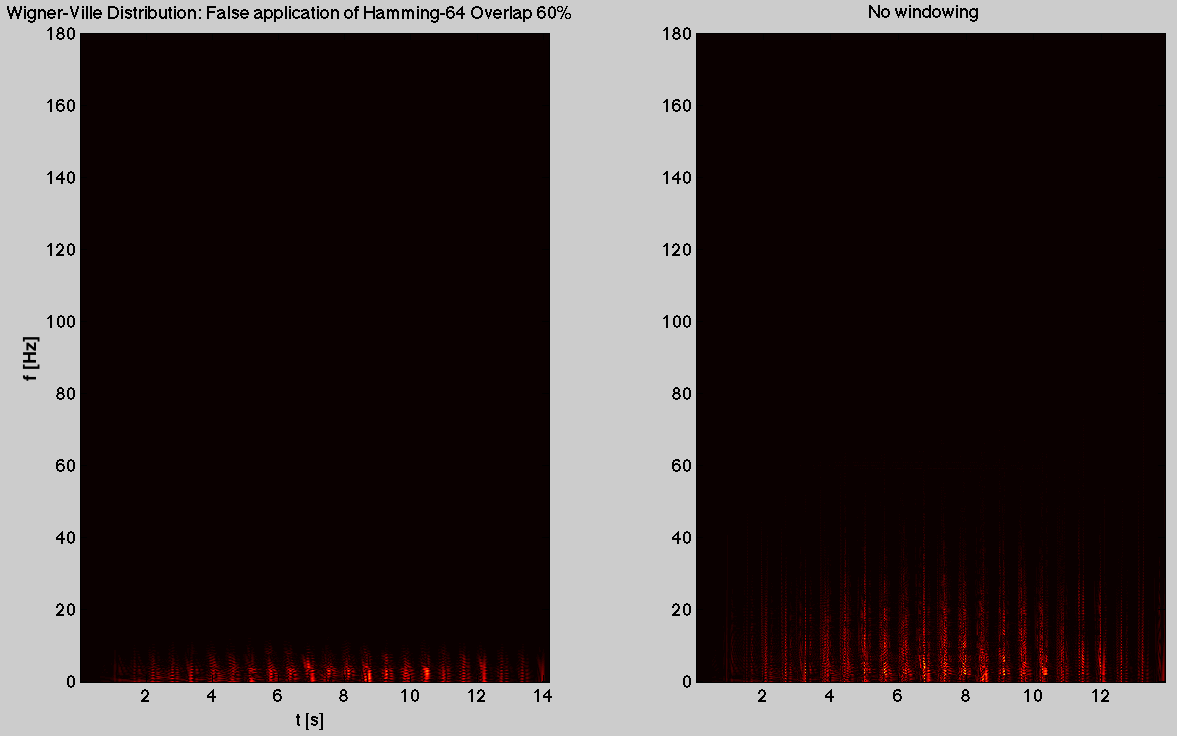
Я знаю, что изображение без окон правильное, так как я вижу там горизонтальную линию 60 Гц, вызванную настройками измерительной системы в базе данных аритмии MIT-BIH. Пациенту 68 лет со старым инфарктом миокарда, поэтому количество ударов в секунду, достигающее 65, соответствует данному методу.

Картина с реализацией моей оригинальной версии Хэмминга-64 не правильная. Человек не будет долго жить с такими ударами в минуту.

Answer 4

2-е расширение ответа на lennon310

data1 = conv(data(1:64),hamming(64)); [B,T,F] = tfrwv(data1, 1:length(data1), length(data1));    
data1 = conv(data(38:101),hamming(64)); [b,t,f] = tfrwv(data1, 1:length(data1), length(data1));

Я не знаю, как я должен объединить кусочки данных от б до б. Матричная диагонализация не кажется подходящим выбором.

Я бегу, используя только hamming(64) для упрощения рассмотрено здесь о реализации диагонализации матрицы

    B = 0; T = 0; F = 0;    
    data1 = conv(data(1 : 64),hamming(64)); [B,T,F] = tfrwv(data1, 1:length(data1), length(data1));    
    for i=1:10
        data1 = conv(data( 1 + i*37 : 64 + i*37 ),hamming(64)); [b,t,f] = tfrwv(data1, 1:length(data1), length(data1));    
        B = blkdiag(B,b); T = [T t]; F = [F; f];
    end

я получил

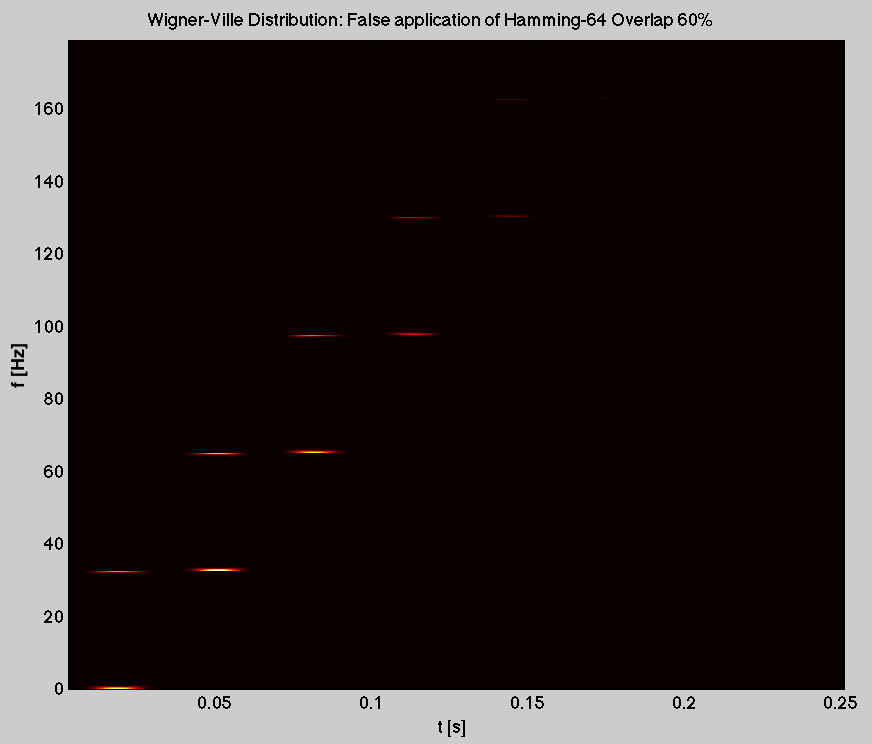
Это неправильный результат. Проблема в том, чтобы понять, какой должна быть матрица B. Как должна выглядеть матрица B после добавления b в B?