Неуправляемая кластеризация с неизвестным количеством кластеров

Question

У меня большой набор векторов в 3 измерениях. Мне нужно сгруппировать их на основе евклидова расстояния так, чтобы все векторы в любом конкретном кластере имели евклидово расстояние между собой меньше, чем пороговое значение "T".

Я не знаю, сколько существует кластеров. В конце могут существовать отдельные векторы, которые не являются частью какого-либо кластера, потому что его евклидово расстояние не меньше, чем "Т" с любым из векторов в пространстве.

Какие существующие алгоритмы / подходы следует использовать здесь?

Answer 1

Вы можете использовать иерархическую кластеризацию. Это довольно простой подход, поэтому существует множество реализаций. Это, например, включено в Scipy Python.

Смотрите, например, следующий скрипт:

import matplotlib.pyplot as plt
import numpy
import scipy.cluster.hierarchy as hcluster

# generate 3 clusters of each around 100 points and one orphan point
N=100
data = numpy.random.randn(3*N,2)
data[:N] += 5
data[-N:] += 10
data[-1:] -= 20

# clustering
thresh = 1.5
clusters = hcluster.fclusterdata(data, thresh, criterion="distance")

# plotting
plt.scatter(*numpy.transpose(data), c=clusters)
plt.axis("equal")
title = "threshold: %f, number of clusters: %d" % (thresh, len(set(clusters)))
plt.title(title)
plt.show()

Который дает результат, похожий на следующее изображение.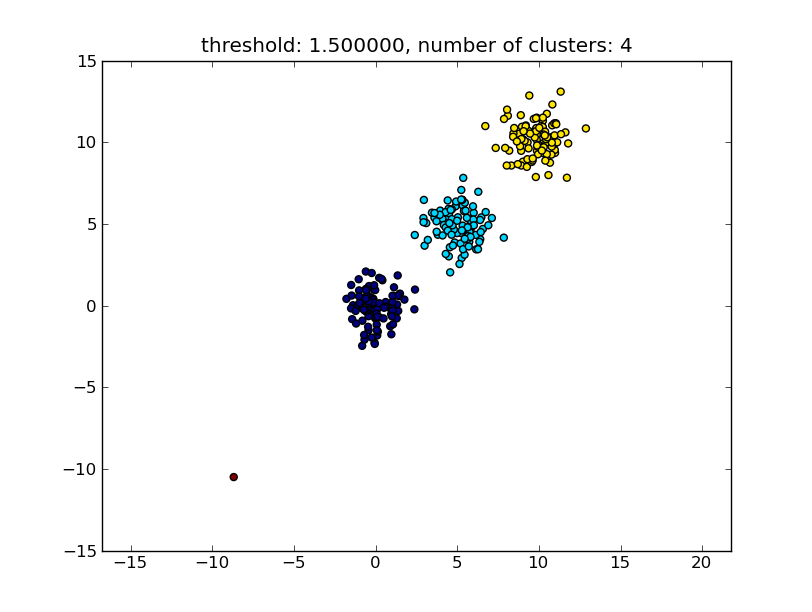

Порог, заданный в качестве параметра, является значением расстояния, на основании которого принимается решение о том, будут ли точки / кластеры объединены в другой кластер. Используемая метрика расстояния также может быть указана.

Обратите внимание, что существуют различные методы для вычисления внутри-/ межкластерного сходства, например, расстояние между ближайшими точками, расстояние между самыми дальними точками, расстояние до центров кластера и так далее. Некоторые из этих методов также поддерживаются модулем иерархической кластеризации scipys ( одиночная / полная / средняя... связь). В соответствии с вашим постом, я думаю, вы хотели бы использовать полную связь.

Обратите внимание, что этот подход также допускает небольшие (одноточечные) кластеры, если они не соответствуют критерию подобия других кластеров, то есть порогу расстояния.

---

Существуют и другие алгоритмы, которые будут работать лучше, и станут актуальными в ситуациях с большим количеством точек данных. Поскольку другие ответы / комментарии предполагают, что Вы могли бы также хотеть взглянуть на алгоритм DBSCAN:

• https://en.wikipedia.org/wiki/DBSCAN
• http://scikit-learn.org/stable/auto_examples/cluster/plot_dbscan.html
• http://scikit-learn.org/stable/modules/generated/sklearn.cluster.DBSCAN.html

---

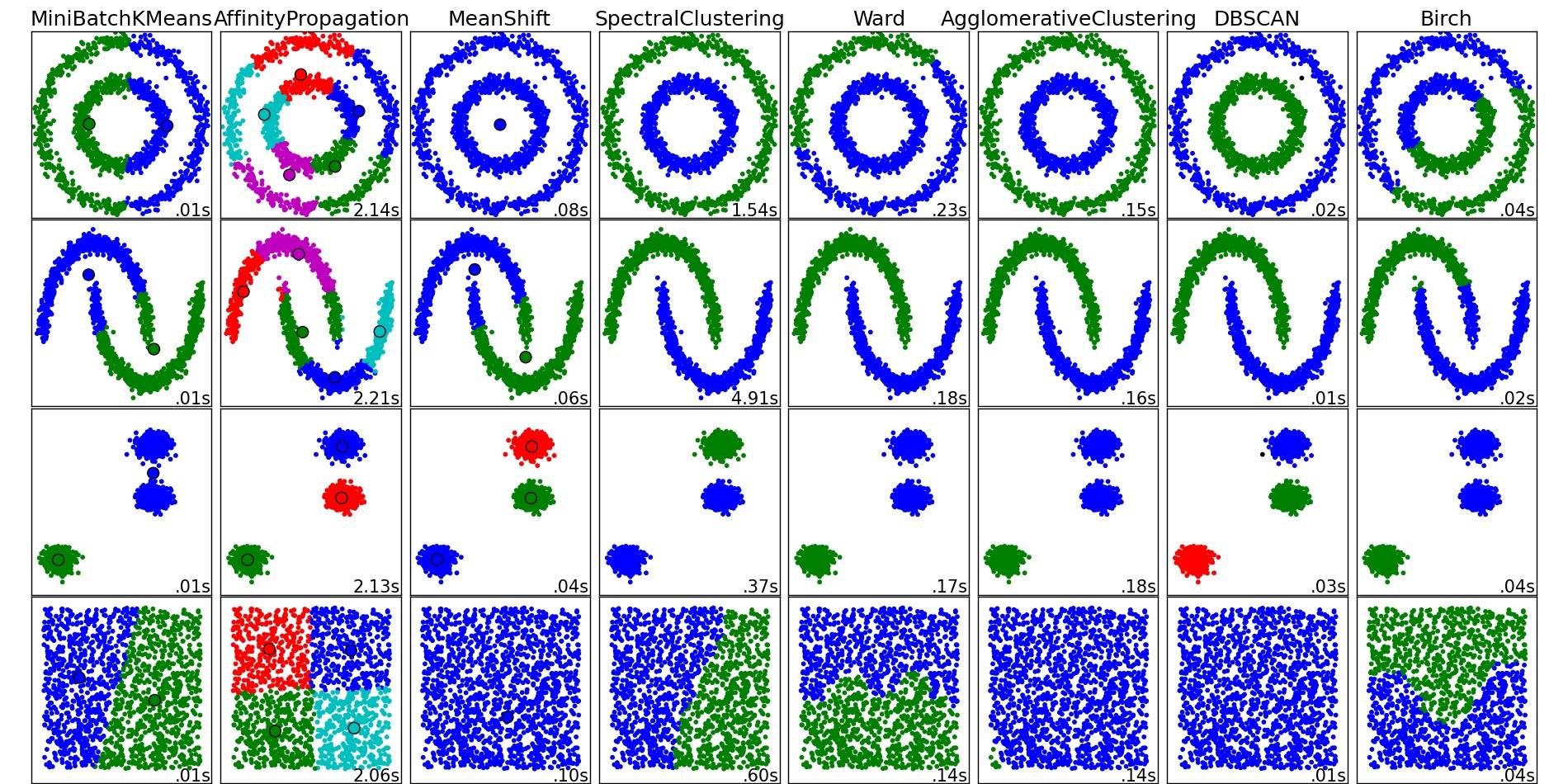
Для хорошего обзора этих и других алгоритмов кластеризации, также взгляните на эту демонстрационную страницу (из библиотеки Python scikit-learn):

• http://scikit-learn.org/stable/modules/clustering.html

Изображение скопировано с этого места:

Как видите, каждый алгоритм делает некоторые предположения о количестве и форме кластеров, которые необходимо учитывать. Будь то неявные предположения, налагаемые алгоритмом, или явные предположения, заданные параметризацией.

Answer 2

В ответе moooeeeep рекомендуется использовать иерархическую кластеризацию. Я хотел уточнить, как выбрать порог кластеризации.

Одним из способов является вычисление кластеризации на основе различных порогов t1, t2, t3,..., а затем вычисление метрики для "качества" кластеризации. Предпосылка состоит в том, что качество кластеризации с оптимальным количеством кластеров будет иметь максимальное значение показателя качества.

Примером метрики хорошего качества, которую я использовал в прошлом, является Calinski-Harabasz. Вкратце: вы вычисляете средние расстояния между кластерами и делите их на расстояния внутри кластера. Оптимальное назначение кластеризации будет иметь кластеры, которые больше всего отделены друг от друга, и кластеры, которые являются "самыми узкими".

Кстати, вам не нужно использовать иерархическую кластеризацию. Вы также можете использовать что-то вроде k- средних, предварительно вычислить его для каждого k, а затем выбрать k, которое имеет наивысший балл Calinski-Harabasz.

Дайте мне знать, если вам нужно больше ссылок, и я поищу на своем жестком диске некоторые бумаги.

Answer 3

Проверьте алгоритм DBSCAN. Это кластеры, основанные на локальной плотности векторов, то есть они не должны быть на расстоянии более чем одного расстояния друг от друга, и могут автоматически определять количество кластеров. Также рассматриваются выбросы, то есть точки с недостаточным числом ε- соседей, которые не являются частью кластера. Страница Википедии ссылается на несколько реализаций.

Answer 4

Используйте ОПТИКУ, которая хорошо работает с большими наборами данных.

ОПТИКА: точки упорядочивания для определения структуры кластеризации Тесно связана с DBSCAN, находит образцы ядра с высокой плотностью и расширяет кластеры из них 1. В отличие от DBSCAN, сохраняет кластерную иерархию для переменного радиуса окрестности. Лучше подходит для использования с большими наборами данных, чем текущая реализация DBSCAN в sklearn.

from sklearn.cluster import OPTICS
db = OPTICS(eps=3, min_samples=30).fit(X)

Точная настройка ЭТС, min_samples согласно вашему требованию.

Answer 5

Я хочу добавить к ответу moooeeeep, используя иерархическую кластеризацию. Это решение работает для меня, хотя выбор порогового значения довольно "случайный". Обратившись к другому источнику и проверив самостоятельно, я получил лучший метод, и порог можно легко выбрать с помощью дендрограммы:

from scipy.cluster import hierarchy
from scipy.spatial.distance import pdist
import matplotlib.pyplot as plt

ori_array = ["Your_list_here"]
ward_array = hierarchy.ward(pdist(ori_array))
dendrogram = hierarchy.dendrogram(hierarchy.linkage(ori_array, method  = "ward"))
plt.title('Dendrogram')
plt.xlabel('Customers')
plt.ylabel('Euclidean distances')
plt.show()

Вы увидите сюжет, подобный этому, нажмите здесь. Затем, проведя горизонтальную линию, скажем, на расстоянии = 1, количество соединений будет вашим желаемым количеством кластеров. Итак, здесь я выбираю порог = 1 для 4 кластеров.

threshold = 1
clusters_list = hierarchy.fcluster(ward_array, threshold, criterion="distance")
print("Clustering list: {}".format(clusters_list))

Теперь каждое значение в cluster_list будет назначенным идентификатором кластера соответствующей точки в ori_array.

Answer 6

У вас может не быть решения: это тот случай, когда расстояние между любыми двумя отдельными точками входных данных всегда больше T. Если вы хотите вычислить количество кластеров только из входных данных, вы можете посмотреть на MCG, иерархическую кластеризацию с критерием автоматической остановки: см. бесплатную статью семинара по адресу https://hal.archives-ouvertes.fr/hal-02124947/document (содержит библиографические ссылки).

Answer 7

Мне нужен был способ «нечеткой сортировки» строк из вывода OCR, когда вывод иногда не по порядку, но внутри блоков строки обычно в порядке. В этом случае элементами для сортировки являются словари, описывающие слова в позиции «x», «y» и с размером «w», «h». Общие алгоритмы кластеризации казались излишними, и мне нужно было поддерживать порядок элементов во время сортировки. Здесь я могу установить допуск tol равным примерно 1/4 межстрочного интервала, и это вызывается с полем «y».

      def fuzzy_lod_sort(lod, field, tol):
    # fuzzy sort lod into bins within +/- tol
    # maintain original order.
    
    # first determine the bins.
    val_list = [d[field] for d in lod]
    vals_sorted = sorted(val_list)
    
    bins_lol = []
    i = 0
    for j, v in enumerate(vals_sorted):
        if not j:
            bins_lol.append([v])
            continue
            
        cur_bin_avg = statistics.mean(bins_lol[i])
        if abs(cur_bin_avg - v) <= tol:
            bins_lol[i].append(v)
            continue
        
        i += 1
        bins_lol.append([v])
        
    # now sort into the bins, maintaining the original order.
    # the bins will be the center of the range of 'y'.
    bins = [statistics.mean(binlist) for binlist in bins_lol]
    
    # initialize the list of bins
    lolod = []
    for _ in range(len(bins)):
        lolod.append([])
    
    for d in lod:
        bin_idx = closest_bin_idx(bins, d[field])
        lolod[bin_idx].append(d)

    # now join the bins.
    result_lod = []
    for lod in lolod:
        result_lod.extend(lod)
    
    return result_lod
    
        
def closest_bin(bins, val):
    return min(bins, key=lambda bin:abs(bin - val))
    
    
def closest_bin_idx(bins, val):
    return bins.index(closest_bin(bins, val))

Проблема в том, что координата «y» вывода OCR основана на контуре вокруг слова, и более позднее слово в той же строке может иметь координату «y», которая ниже, чем у более раннего слова. Так что полная сортировка по 'y' не работает. Это очень похоже на алгоритм кластеризации, но намерение немного отличается. Меня не интересует статистика точек данных, но меня интересует, какой именно кластер размещен каждый, а также важно поддерживать первоначальный порядок.

Возможно, существует какой-то способ нечеткой сортировки с использованием встроенных средств сортировки, и это может быть альтернативой параметрам кластеризации для одномерных задач.